

2024年高考数学第一轮复习专题训练第七章 §7.3 空间点、直线、平面之间的位置关系
展开§7.3 空间点、直线、平面之间的位置关系
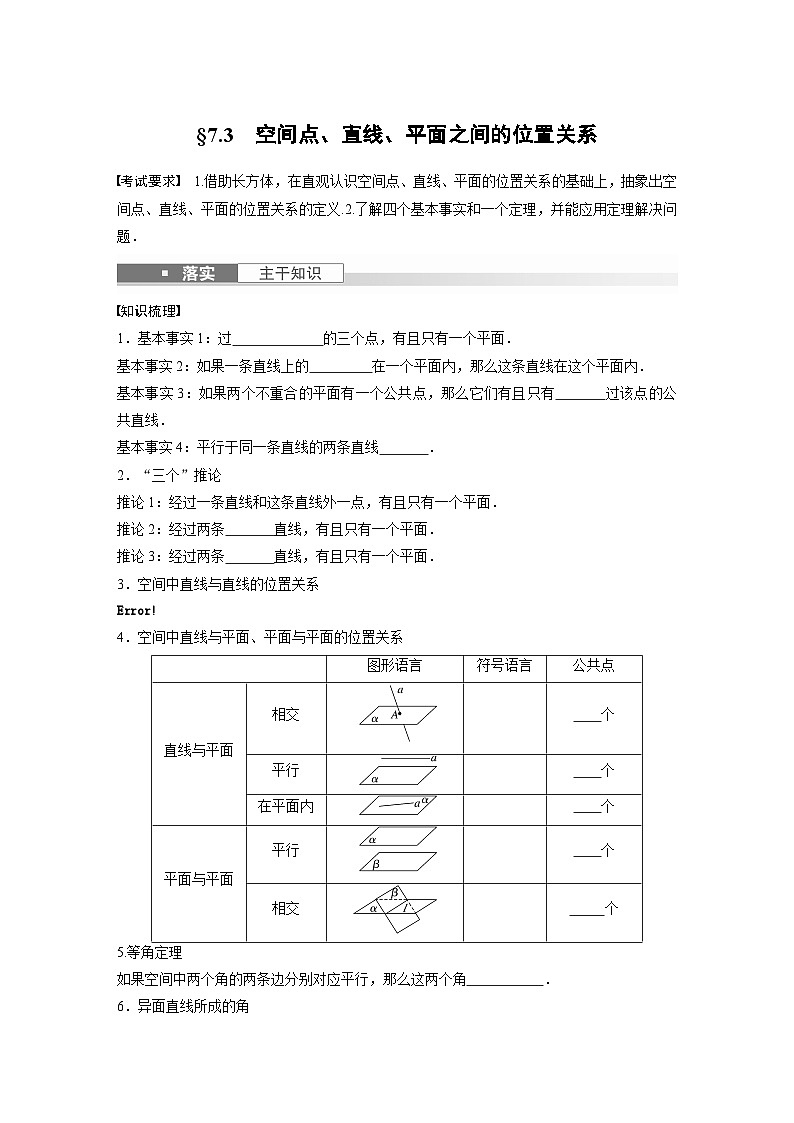
考试要求 1.借助长方体,在直观认识空间点、直线、平面的位置关系的基础上,抽象出空间点、直线、平面的位置关系的定义.2.了解四个基本事实和一个定理,并能应用定理解决问题.
知识梳理
1.基本事实1:过 的三个点,有且只有一个平面.
基本事实2:如果一条直线上的 在一个平面内,那么这条直线在这个平面内.
基本事实3:如果两个不重合的平面有一个公共点,那么它们有且只有 过该点的公共直线.
基本事实4:平行于同一条直线的两条直线 .
2.“三个”推论
推论1:经过一条直线和这条直线外一点,有且只有一个平面.
推论2:经过两条 直线,有且只有一个平面.
推论3:经过两条 直线,有且只有一个平面.
3.空间中直线与直线的位置关系
4.空间中直线与平面、平面与平面的位置关系
| 图形语言 | 符号语言 | 公共点 | |
直线与平面 | 相交 |
| 个 | |
平行 |
| 个 | ||
在平面内 |
| 个 | ||
平面与平面 | 平行 |
| 个 | |
相交 |
| 个 | ||
5.等角定理
如果空间中两个角的两条边分别对应平行,那么这两个角 .
6.异面直线所成的角
(1)定义:已知两条异面直线a,b,经过空间任一点O分别作直线a′∥a,b′∥b,我们把直线a′与b′所成的角叫做异面直线a与b所成的角(或夹角).
(2)范围: .
常用结论
1.过平面外一点和平面内一点的直线,与平面内不过该点的直线是异面直线.
2.分别在两个平行平面内的直线平行或异面.
思考辨析
判断下列结论是否正确(请在括号中打“√”或“×”)
(1)没有公共点的两条直线是异面直线.( )
(2)直线与平面的位置关系有平行、垂直两种.( )
(3)如果两个平面有三个公共点,则这两个平面重合.( )
(4)两两相交的三条直线共面.( )
教材改编题
1.(多选)如图是某正方体的平面展开图,则在这个正方体中,下列说法正确的是( )
A.BM与ED平行
B.CN与BM成60°角
C.CN与BE是异面直线
D.DM与BN是异面直线
2.已知a,b是异面直线,直线c平行于直线a,那么c与b( )
A.一定是异面直线
B.一定是相交直线
C.不可能是平行直线
D.不可能是相交直线
3. 如图,在三棱锥A-BCD中,E,F,G,H分别是棱AB,BC,CD,DA的中点,则
(1)当AC,BD满足条件________时,四边形EFGH为菱形;
(2)当AC,BD满足条件________时,四边形EFGH为正方形.
题型一 基本事实的应用
例1 已知在正方体ABCD-A1B1C1D1中,E,F分别为D1C1,C1B1的中点,AC∩BD=P,A1C1∩EF=Q.
求证:(1)D,B,F,E四点共面;
(2)若A1C交平面DBFE于点R,则P,Q,R三点共线;
(3)DE,BF,CC1三线交于一点.
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
思维升华 共面、共线、共点问题的证明
(1)共面:先确定一个平面,然后再证其余的线(或点)在这个平面内.
(2)共线:先由两点确定一条直线,再证其他各点都在这条直线上.
(3)共点:先证其中两条直线交于一点,再证其他直线经过该点.
跟踪训练1 (1)如图,α∩β=l,A,B∈α,C∈β,且A,B,C∉l,直线AB∩l=M,过A,B,C三点的平面记作γ,则γ与β的交线必经过( )
A.点A
B.点B
C.点C但不过点M
D.点C和点M
(2)如图所示,平面ABEF⊥平面ABCD,四边形ABEF与ABCD都是直角梯形,∠BAD=∠FAB=90°,BC∥AD且BC=AD,BE∥AF且BE=AF,G,H分别为FA,FD的中点.
①证明:四边形BCHG是平行四边形;
②C,D,F,E四点是否共面?为什么?
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
题型二 空间位置关系的判断
命题点1 空间位置关系的判断
例2 (1)(多选)下列推断中,正确的是( )
A.M∈α,M∈β,α∩β=l⇒M∈l
B.A∈α,A∈β,B∈α,B∈β⇒α∩β=AB
C.l⊄α,A∈l⇒A∉α
D.A,B,C∈α,A,B,C∈β,且A,B,C不共线⇒α,β重合
(2)(2023·龙岩模拟)若a和b是异面直线,b和c是异面直线,则a和c的位置关系是( )
A.异面或平行 B.异面或相交
C.异面 D.相交、平行或异面
听课记录:______________________________________________________________
________________________________________________________________________
命题点2 异面直线所成的角
例3 (1)如图所示,圆柱O1O2的底面半径为1,高为2,AB是一条母线,BD是圆O1的直径,C是上底面圆周上一点,∠CBD=30°,则异面直线AC与BD所成角的余弦值为( )
A. B. C. D.
(2)(2023·长治模拟)如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=CC1=2,E为BB1上一点,平面AEC1将三棱柱分为上、下体积相等的两部分,则AE与B1C1所成角的余弦值为( )
A. B. C. D.
听课记录:______________________________________________________________
________________________________________________________________________
思维升华 (1)点、直线、平面位置关系的判定,注意构造几何体(长方体、正方体)模型来判断,常借助正方体为模型.
(2)求异面直线所成角的方法
方法 | 解读 |
平移法 | 将异面直线中的某一条平移,使其与另一条相交,一般采用图中已有的平行线或者作平行线, 形成三角形求解 |
补形法 | 在该几何体的某侧补接上同样一个几何体,在这两个几何体中找异面直线相应的位置,形成三角形求解 |
跟踪训练2 (1)(多选)如图所示,在正方体ABCD-A1B1C1D1中,M,N分别为棱C1D1,C1C的中点,以下四个选项正确的是( )
A.直线AM与CC1是相交直线
B.直线AM与BN是平行直线
C.直线BN与MB1是异面直线
D.直线AM与DD1是异面直线
(2)如图,在圆锥SO中,AB,CD为底面圆的两条直径,AB∩CD=O,且AB⊥CD,SO=OB=3,SE=SB,则异面直线SC与OE所成角的正切值为( )
A. B. C. D.
(3)平面α过正方体ABCD-A1B1C1D1的顶点A,α∥平面CB1D1,α∩平面ABCD=m,α∩平面ABB1A1=n,则m,n所成角的正弦值为( )
A. B. C. D.
题型三 空间几何体的切割(截面)问题
例4 (1)(多选)用一个平面α截正方体,把正方体分为体积相等的两部分,则下列结论正确的是( )
A.这两部分的表面积一定不相等
B.截面不会是三角形
C.截面不会是五边形
D.截面可以是正六边形
(2)已知直四棱柱ABCD-A1B1C1D1的棱长均为2,∠BAD=60°,以D1为球心,为半径的球面与侧面BCC1B1的交线长为________.
听课记录:______________________________________________________________
________________________________________________________________________
思维升华 (1)作截面应遵循的三个原则:①在同一平面上的两点可引直线;②凡是相交的直线都要画出它们的交点;③凡是相交的平面都要画出它们的交线.
(2)作交线的方法有如下两种:①利用基本事实3作交线;
②利用线面平行及面面平行的性质定理去寻找线面平行及面面平行,然后根据性质作出交线.
跟踪训练3 (1)(多选)在正方体ABCD-A1B1C1D1中,E,F分别在B1B和C1C上(异于端点),则过三点A,F,E的平面被正方体截得的图形(截面)可能是( )
A.矩形 B.菱形 C.正方形 D.梯形
(2)如图,在正方体ABCD-A1B1C1D1中,E是BC的中点,平面α经过直线BD且与直线C1E平行,若正方体的棱长为2,则平面α截正方体所得的多边形的面积为________.
2024高考数学第一轮复习:8.2 空间点、直线、平面之间的位置关系(原卷版): 这是一份2024高考数学第一轮复习:8.2 空间点、直线、平面之间的位置关系(原卷版),共13页。试卷主要包含了与平面有关的基本事实及推论,基本事实4和等角定理,异面直线所成的角等内容,欢迎下载使用。
2024高考数学第一轮复习:8.2 空间点、直线、平面之间的位置关系(解析版): 这是一份2024高考数学第一轮复习:8.2 空间点、直线、平面之间的位置关系(解析版),共32页。试卷主要包含了与平面有关的基本事实及推论,基本事实4和等角定理,异面直线所成的角等内容,欢迎下载使用。
2024高考数学一轮复习讲义(步步高版)第七章 §7.3 空间点、直线、平面之间的位置关系: 这是一份2024高考数学一轮复习讲义(步步高版)第七章 §7.3 空间点、直线、平面之间的位置关系,共25页。试卷主要包含了等角定理等内容,欢迎下载使用。












