新高考物理三轮冲刺知识讲练与题型归纳专题07 圆周运动（含解析）

这是一份新高考物理三轮冲刺知识讲练与题型归纳专题07 圆周运动（含解析），共26页。
TOC \ "1-3" \h \z \u \l "_Tc127957931" 题型一 圆周运动的运动学问题 PAGEREF _Tc127957931 \h 1
\l "_Tc127957932" 题型二 圆周运动的动力学问题 PAGEREF _Tc127957932 \h 5
\l "_Tc127957933" 题型三 竖直面内圆周运动的两类模型问题 PAGEREF _Tc127957933 \h 12
\l "_Tc127957934" 题型四 圆周运动中的两类临界问题 PAGEREF _Tc127957934 \h 18
[考点分析]
题型一 圆周运动的运动学问题
1．线速度：描述物体圆周运动快慢的物理量．v＝eq \f(Δs,Δt)＝eq \f(2πr,T).
2．角速度：描述物体绕圆心转动快慢的物理量．ω＝eq \f(Δθ,Δt)＝eq \f(2π,T).
3．周期和频率：描述物体绕圆心转动快慢的物理量．T＝eq \f(2πr,v)，T＝eq \f(1,f).
4．向心加速度：描述速度方向变化快慢的物理量．an＝rω2＝eq \f(v2,r)＝ωv＝eq \f(4π2,T2)r.
5．相互关系：(1)v＝ωr＝eq \f(2π,T)r＝2πrf.(2)an＝eq \f(v2,r)＝rω2＝ωv＝eq \f(4π2,T2)r＝4π2f2r.
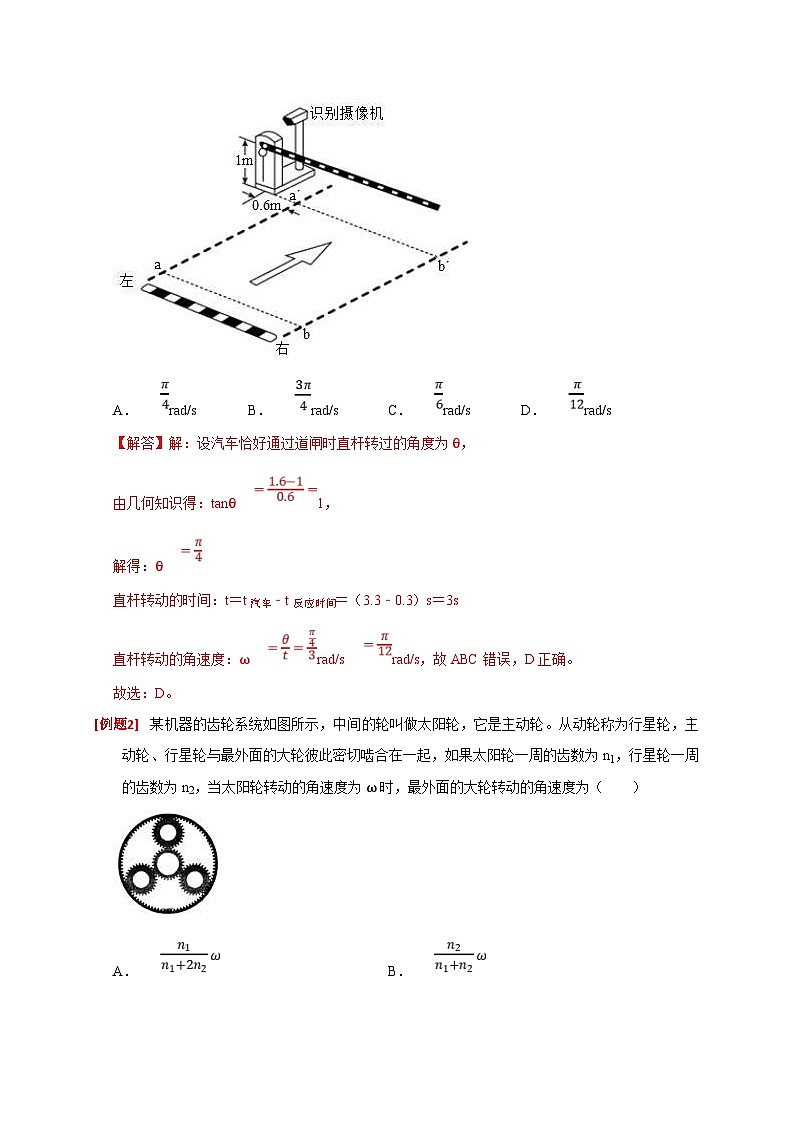
如图为车牌自动识别系统的直杆道闸，离地面高为1m的细直杆可绕O在竖直面内匀速转动。汽车从自动识别线ab处到达直杆处的时间为3.3s，自动识别系统的反应时间为0.3s；汽车可看成高1.6m的长方体，其左侧面底边在aa′直线上，且O到汽车左侧面的距离为0.6m，要使汽车安全通过道闸，直杆转动的角速度至少为（ ）
A．rad/sB．rad/sC．rad/sD．rad/s
【解答】解：设汽车恰好通过道闸时直杆转过的角度为θ，
由几何知识得：tanθ1，
解得：θ
直杆转动的时间：t＝t汽车﹣t反应时间＝（3.3﹣0.3）s＝3s
直杆转动的角速度：ωrad/srad/s，故ABC错误，D正确。
故选：D。
某机器的齿轮系统如图所示，中间的轮叫做太阳轮，它是主动轮。从动轮称为行星轮，主动轮、行星轮与最外面的大轮彼此密切啮合在一起，如果太阳轮一周的齿数为n1，行星轮一周的齿数为n2，当太阳轮转动的角速度为ω时，最外面的大轮转动的角速度为（ ）
A．B．
C．D．
【解答】解：主动轮、行星轮与大轮分别用A、B、C表示，由图可知，A与B为齿轮传动，所以线速度大小相等，B与C也是车轮传动，线速度也相等，所以A与B、C的线速度是相等的；有线速度关系可知：
则：
由图可知：RC＝2RB+RA
A、B与C的线速度相同，得：ωRA＝ω′RC
联立可得：．故A正确，BCD错误
故选：A。
无级变速是在变速范围内任意连续变换速度的变速系统．如图所示是无级变速模型示意图，主动轮、从动轮中间有一个滚轮，各轮间不打滑，通过滚轮位置改变实现无级变速。A、B为滚轮轴上两点，则（ ）
A．从动轮和主动轮转动方向始终相反
B．滚轮在A处，从动轮转速大于主动轮转速
C．滚轮在B处，从动轮转速大于主动轮转速
D．滚轮从A到B，从动轮转速先变大后变小
【解答】解：A、从动轮和主动轮转动方向始终相同，故A错误；
B、角速度ω＝2πn，则主动轮的线速度v1＝r1ω1＝2πr1n1，从动轮的线速度v2＝r2ω1＝2πr2n2．因为主动轮和从动轮的线速度相等，则2πr1n1＝2πr2n2，所以n2＝n1.，滚轮在A处，r1＞r2，从动轮转速大于主动轮转速，故B正确；
C、在B处，r1＜r2，从动轮转速，小于主动轮转速，故C错误；
D、滚轮从A到B，r1逐渐减小，r2逐渐增大，故从动轮转速逐渐减小，故D错误；
故选：B。
由于高度限制，车库出入口采用图所示的曲杆道闸，道闸由转动杆OP与横杆PQ链接而成，P、Q为横杆的两个端点．在道闸抬起过程中，杆PQ始终保持水平．杆OP绕O点从与水平方向成30°匀速转动到60°的过程中，下列说法正确的是（ ）
A．P点的线速度大小不变
B．P点的加速度方向不变
C．Q点在竖直方向做匀速运动
D．Q点在水平方向做匀速运动
【解答】解：A、由题知杆OP绕O点从与水平方向成30°匀速转动到60°，则P点绕O点做匀速圆周运动，则P点的线速度大小不变。故A正确；
B、由题知杆OP绕O点从与水平方向成30°匀速转动到60°，则P点绕O点做匀速圆周运动，P点的加速度方向时刻指向O点。故B错误；
C、Q点在竖直方向的运动与P点相同，相对于O点在竖直方向的位置y关于时间t的关系为
y＝lOP⋅sin（ωt）
则可看出Q点在竖直方向不是匀速运动。故C错误；
D．Q点相对于O点在水平方向的位置x关于时间t的关系为
x＝lOP⋅cs（ωt）+lPQ
则可看出Q点在水平方向也不是匀速运动。故D错误．
故选：A。
如图所示为旋转脱水拖把结构图。把拖把头放置于脱水筒中，手握固定套杆向下运动，固定套杆就会给旋转杆施加驱动力，驱动旋转杆、拖把头和脱水筒一起转动，把拖把上的水甩出去。旋转杆上有长度为35cm的螺杆，螺杆的螺距（相邻螺纹之间的距离）为d＝5cm，拖把头的托盘半径为10cm，拖布条的长度为6cm，脱水筒的半径为12cm。某次脱水时，固定套杆在1s内匀速下压了35cm，该过程中拖把头匀速转动，则下列说法正确的是（ ）
A．拖把头的周期为7s
B．拖把头转动的角速度为14πrad/s
C．紧贴脱水筒内壁的拖布条上附着的水最不容易甩出
D．旋转时脱水筒内壁与托盘边缘处的点向心加速度之比为5：6
【解答】解：A、旋转杆上有长度为35cm的螺杆，相邻螺纹之间的距离为d＝5cm，所以共7圈，固定套杆在1s内匀速下压了35cm，所以1s转了7个周期，故周期为：Ts，故A错误；
B、根据周期和角速度的关系式：，故B正确；
C、紧贴脱水筒内壁的拖布条半径最大，根据a＝ω2r，半径越大，向心加速度越大，需要的向心力越大，越容易甩出，故C错误；
D、脱水筒内壁半径为12cm，托盘边缘半径为10cm，根据a＝ω2r，向心加速度之比为
故
故D错误。
故选：B。
题型二 圆周运动的动力学问题
1．向心力的来源
向心力是按力的作用效果命名的，可以是重力、弹力、摩擦力等各种力，也可以是几个力的合力或某个力的分力，因此在受力分析中要避免再另外添加一个向心力．
2．向心力的确定
(1)确定圆周运动的轨道所在的平面，确定圆心的位置．
(2)分析物体的受力情况，找出所有的力沿半径方向指向圆心的合力，就是向心力．
3．向心力的公式Fn＝man＝meq \f(v2,r)＝mω2r＝mreq \f(4π2,T2)＝mr4π2f2
解决圆周运动问题的主要步骤
(1)审清题意，确定研究对象；明确物体做圆周运动的平面是至关重要的一环；
(2)分析物体的运动情况，即物体的线速度、角速度、周期、轨道平面、圆心、半径等；
(3)分析物体的受力情况，画出受力分析图，确定向心力的来源；
(4)根据牛顿运动定律及向心力公式列方程．
（多选）如图所示，足够大的水平圆台中央固定一光滑竖直细杆，原长为L的轻质弹簧套在竖直杆上，质量均为m的光滑小球A、B用长为L的轻杆及光滑铰链相连，小球A穿过竖直杆置于弹簧上。让小球B以不同的角速度ω绕竖直杆匀速转动，当转动的角速度为ω0时，小球B刚好离开台面。弹簧始终在弹性限度内，劲度系数为k，重力加速度为g，则（ ）
A．小球均静止时，弹簧的长度为L
B．角速度ω＝ω0时，小球A对弹簧的压力为mg
C．角速度ω0
D．角速度从ω0继续增大的过程中，小球A对弹簧的压力不变
【解答】解：A、光滑小球均静止时，则可知，杆没有作用力，否则B球不可能平衡的，对A受力分析，重力与弹簧的弹力，处于平衡，依据胡克定律，那么弹簧的形变量△x，因此弹簧的长度为L′＝L，故A正确；
B、角速度ω＝ω0时，球B在杆及重力作用下，提供向心力，做匀速圆周运动，那么，杆对小球A有作用力，因此弹簧对A的支持力大于mg，则球A对弹簧的压力也大于mg，故B错误；
C、当转动的角速度为ω0时，小球B刚好离开台面，对B分析，杆的拉力与重力的合力提供向心力，如下图所示：
根据矢量的合成法则，结合牛顿第二定律，则有mLcsθ，
对AB整体分析，弹簧的弹力F′＝2mg
依据胡克定律，则弹簧的形变量L″，
根据几何知识，则有：sinθ
综上所述，解得：ω0，故C正确；
D、由上分析，可知，当转动的角速度为ω0时，小球B刚好离开台面，弹簧弹力等于2mg，当角速度从ω0继续增大的过程中，弹簧弹力仍等于2mg，因此小球A对弹簧的压力不会变，故D正确；
故选：ACD。
（多选）如图所示，半径为R的半球形容器固定在可以绕竖直轴旋转的水平转台上，转台转轴与过容器球心O的竖直线重合，转台以一定角速度ω匀速旋转。有两个质量均为m的小物块落入容器内，经过一段时间后，两小物块都随容器一起转动且相对容器内壁静止，两物块和球心O点的连线相互垂直，且A物块和球心O点的连线与竖直方向的夹角θ＝60°，已知重力加速度大小为g，则下列说法正确的是（ ）
A．若A物块受到的摩擦力恰好为零，B物块受到的摩擦力的大小为
B．若A物块受到的摩擦力恰好为零，B物块受到的摩擦力的大小为
C．若B物块受到的摩擦力恰好为零，A物块受到的摩擦力的大小为
D．若B物块受到的摩擦力恰好为零，A物块受到的摩擦力的大小为
【解答】解：AB、当A摩擦力恰为零时，物块与圆心连线与竖直方向的夹角为60°，受力如图1所示，
图1
根据牛顿第二定律得：
mgtan60°＝mrω2
r＝Rsin60°
此时B滑块有沿斜面向上滑的趋势，摩擦力沿罐壁切线向下，受力如图2所示。
图2
竖直方向上：Ncs30°﹣fsin30°﹣mg＝0
水平方向上：Nsin30°+fcs30°＝mr′ω2
其中r′＝Rsin30°，联立解得：f，故A错误，B正确；
CD、当B摩擦力恰为零时，物块与圆心连线与竖直方向的夹角为300
根据牛顿第二定律得：mgtan30°＝mrω2
其中r＝Rsin30°
此时A滑块有沿斜面向下滑的趋势，摩擦力沿罐壁切线向上，
竖直方向上：Ncs60°+fsin60°﹣mg＝0
水平方向上：Nsin60°﹣fcs60°＝mr′ω2
r′＝Rsin60°，联立解得：f，故C正确。D错误；
故选：BC。
如图所示，在竖直面内固定三枚钉子a、b、c，三枚钉子构成边长d＝10cm的等边三角形，其中钉子a、b沿着竖直方向。长为L＝0.3m的细线一端固定在钉子a上，另一端系着质量m＝200g的小球，细线拉直与边ab垂直，然后将小球以v0m/s的初速度竖直向下抛出，小球可视为质点，不考虑钉子的粗细，重力加速度g＝10m/s2，细线碰到钉子c后，物块到达最高点时，细线拉力大小为（ ）
A．0NB．1NC．2ND．3N
【解答】解：设物块到达量高点速度为v，根据机械能守恒得
mv02mv2+mgh
h＝L﹣d﹣dLd
代入数据联立解得vm/s
根据牛顿第二定律
F+mg＝m
解得细线拉力大小为
F＝mmg＝0.2N﹣0.2×10N＝2N
故选：C。
（多选）如图所示为波轮式洗衣机的工作原理示意图，当甩衣桶在电机的带动下高速旋转时，衣服紧贴在甩衣桶器壁上，从而迅速将水甩出。衣服（带水，可视为质点）质量为m，衣服和器壁的动摩擦因数约为μ，甩衣桶的半径为γ，洗衣机的外桶的半径为R，当角速度达到ω0时，衣服上的水恰好被甩出，假设滑动摩擦力和最大静摩擦力相等，重力加速度为g，则下列说法正确的是（ ）
A．衣服（带水）做匀变速曲线运动
B．电动机的角速度至少为时，衣服才掉不下来
C．当ω＝ω0时，水滴下落高度打到外筒上
D．当ω＝ω0时，水滴下落高度打到外筒上
【解答】A.衣服（带水）做变速曲线运动，因为其向心加速度也是变化的，故A错误；
B.竖直方向，根据平衡条件有mg＝μN
由于弹力提供向心力，由牛顿第二定律有
N＝mω02r
联立解得
ω0
故B正确；
CD.当ω＝ω0时，水滴打到外筒上，则水滴下落高度为h，根据平抛运动规律有
h
x＝vt
r2+x2＝R2
v＝rω0
联立解得
h
故C错误，D正确。
故选：BD。
现将等宽双线在水平面内绕制成如图1所示轨道，两段半圆形轨道半径均为Rm，两段直轨道AB、A'B长度均为l＝1.35m。在轨道上放置个质量m＝0.1kg的小圆柱体，如图2所示，圆柱体与轨道两侧相切处和圆柱截面圆心O连线的夹角θ为120°，如图3所示，两轨道与小圆柱体的动摩擦因数均为μ＝0.5，小圆柱尺寸和轨道间距相对轨道长度可忽略不计，初始时小圆柱位于A点处，现使之获得沿直轨道AB方向的初速度v0。求：
（1）小圆柱沿AB运动时，内外轨道对小圆柱的摩擦力f1、f2的大小；
（2）当v0＝6m/s，小圆柱刚经B点进入圆弧轨道时，外轨和内轨对小圆柱的压力N1、N2的大小；
（3）为了让小圆柱不脱离内侧轨道，v0的最大值，以及在v0取最大值情形下小圆柱最终滑过的路程s。
【解答】解：（1）圆柱体与轨道两侧相切处和圆柱截面面圆心O连线的夹角θ为120°，根据对称性可知，两侧弹力大小均与重力相等为1N，内外轨道对小圆柱的摩擦力为：f1＝f2＝μN，
解得：f1＝f2＝0.5N
（2）当v0＝6m/s，小圆柱刚经B点进入圆弧轨道时，根据动能定理可得：
mv2m（f1+f2）l
解得：v＝3m/s
在B点受力分析：N1sin60°﹣N2sin60°＝m；N1cs60°+N2cs60°＝mg
联立解得：N1＝1.3N，N2＝0.7N
（3）为了让小圆柱不脱离内侧轨道，v0最大时，在B点：N'1sin60°＝m，N'1cs60°＝mg
根据动能定理可得：mm（f1+f2）l
联立解得：v0mm/s
在圆弧上受摩擦力仍为：f＝（f1+f2）＝μ（N1+N2），解得：f＝1N
根据动能定理可知：mfs，解得：s＝2.85m
答：（1）小圆柱沿AB运动时，内外轨道对小圆柱的摩擦力f1、f2的大小都为0.5N；
（2）外轨和内轨对小圆柱的压力N1、N2的大小分别为1.3N，0.7N；
（3）为了让小圆柱不脱离内侧轨道，v0的最大值为m/s，以及在v0取最大值情形下小圆柱最终滑过的路程s为2.85m。
题型三 竖直面内圆周运动的两类模型问题
1．在竖直平面内做圆周运动的物体，按运动到轨道最高点时的受力情况可分为两类：一是无支撑(如球与绳连接、沿内轨道运动的过山车等)，称为“绳(环)约束模型”，二是有支撑(如球与杆连接、在弯管内的运动等)，称为“杆(管)约束模型”．
2．绳、杆模型涉及的临界问题
如图甲，ABC为竖直放置的半径为0.1m的半圆形轨道，在轨道的最低点和最高点A、C各安装了一个压力传感器，可测定小球在轨道内侧，通过这两点时对轨道的压力FA和FC．质量为0.1kg的小球，以不同的初速度v由A点冲入ABC轨道．（g取10m/s2）
（1）若轨道ABC光滑，则小球能通过最高点C的最小速度多大？
（2）若轨道ABC光滑，小球均能通过C点．试推导FC随FA变化的关系式，并在图乙中画出其图线；
（3）若FC和FA的关系图线如图丙所示，求：当FA＝13N时小球滑经A点时的速度vA，以及小球由A滑至C的过程中损失的机械能
【解答】解：（1）在C点重力恰好提供向心力时速度最小：

解得：

（2）由牛顿第三定律可知，小球在A、C两点所受轨道的弹力大小：
NA＝FA，NC＝FC
在A点，由牛顿第二定律得：
NA﹣mg＝m①
在C点，由牛顿第二定律得：
NC+mg＝m②
对A至C的过程，由动能定理得：
﹣mg•2Rmm③
联立①②③得：
NA﹣NC＝6mg
即FC＝FA﹣6N
图线如右图所示：
（3）对A至C的过程，由动能定理得：
Wf﹣mg•2Rmm④
联立①②④得：
Wfmm2mgR（2mg﹣FA+FC）R+2mgR…⑤
解得：
Wf＝﹣0.2J
vA＝2m/s
由功能关系得，损失的机械能为0.2J；
答：（1）若轨道ABC光滑，则小球能通过最高点C的最小速度为1m/s；
（2）若轨道ABC光滑，小球均能通过C点．FC随FA变化的关系式为FC＝FA﹣6，其图线如图所示；
（3）当FA＝13N时小球滑经A点时的速度为2m/s，小球由A滑至C的过程中损失的机械能为0.2J．
（多选）如图甲所示，轻杆一端固定在O点，另一端固定质量为m的小球。现让小球在竖直平面内做圆周运动，小球运动到最高点时，杆与小球间弹力大小为F，速度大小为v，其F﹣v2图象如图乙所示。则（ ）
A．小球做圆周运动的半径R
B．当地的重力加速度大小g
C．v2＝c时，小球受到的弹力方向向上
D．v2＝2b时，小球受到的弹力大小与重力大小相等
【解答】解：A、由图乙知，若v＝0，则F＝mg＝a．当F＝0时，v2＝b，则小球在最高点时，当F＝0，有：mg＝mm，联立解得R，故A正确；
B、v2＝0时，根据牛顿第二定律得：mg﹣F＝m0，则F＝mg＝a，所以：g．故B正确。
C、由图可知：当v2＜b时，杆对小球弹力方向向上，当v2＞b时，杆对小球弹力方向向下，所以当v2＝c时，杆对小球弹力方向向下，故C错误；
D、若v2＝2b时。由牛顿第二定律有 F+mg＝mm，结合A项分析解得 F＝mg＝a，故D正确。
故选：ABD。
（多选）如图所示，水平的木板B托着木块A一起在竖直平面内做匀速圆周运动，从水平位置a沿逆时针方向运动到最高点b的过程中（ ）
A．B对A的支持力越来越大B．B对A的支持力越来越小
C．B对A的摩擦力越来越小D．B对A的摩擦力越来越大
【解答】解：A在运动的过程中受重力、支持力、静摩擦力，三个力的合力提供向心力。合力沿水平方向的分力等于A所受的摩擦力，合力沿竖直方向的分力等于重力和支持力的合力，合力的大小不变，由a到b的运动过程中，合力沿水平方向的分力减小，所以摩擦力减小。合力沿竖直方向的分力逐渐增大，所以支持力逐渐减小。故B、C正确，A、D错误。
故选：BC。
摆动是生活中常见的运动形式，秋千、钟摆的运动都是我们熟悉的摆动。摆的形状各异，却遵循着相似的规律。
（1）如图1所示，一个摆的摆长为L，小球质量为m，拉起小球使摆线与竖直方向夹角为θ时将小球由静止释放，忽略空气阻力。
a．求小球运动到最低点时绳对球的拉力的大小F。
b．如图2所示，当小球运动到摆线与竖直方向夹角为α（α＜θ）时，求此时小球的角速度大小ω1。
（2）如图3所示，长为L的轻杆，一端可绕固定在O点的光滑轴承在竖直平面内转动，在距O点为和L处分别固定一个质量为m、可看作质点的小球，忽略轻杆的质量和空气阻力。
a．将杆与小球组成的系统拉到与竖直方向成θ角的位置由静止释放，当系统向下运动到与竖直方向夹角为α（α＜θ）时，求此时系统的角速度大小ω2。
b．若θ较小，系统的运动可看作简谐运动，对比ω2和ω1的表达式，参照单摆的周期公式T＝2π，写出此系统做简谐运动的周期的表达式，并说明依据。
【解答】解：（1）a.根据机械能守恒定律可得
mgL （1﹣csθ）mv2
在最低点根据牛顿第二定律
F﹣mg＝m
解得
F＝mg （3﹣2csθ）
b.根据机械能守恒定律可得
mgL （csα﹣csθ）mv12
角速度为ω1
联立解得
ω1
（2）a.根据机械能守恒定律可得
mgL （csα﹣csθ）+mg （csα﹣csθ）mv22mv2′2
其中
v2＝ω2L，v'2＝ω2
代入解得
ω2
b.此系统做简谐运动的周期为T'＝2
对比ω2和ω1的表达式可得

α可以表示系统运动过程中的任意位置对应的角度，可知两个系统在运动过程中任意位置的角速度大小均满足

因此

可得
T'T＝2
答：（1）a．小球运动到最低点时绳对球的拉力的大小为mg （3﹣2csθ）。
b.此时小球的角速度大小为。
（2）a．此时系统的角速度大小为。
b．此系统做简谐运动的周期的表达式为T'＝2，依据见解析。
（多选）一端连在光滑固定轴上，可在竖直平面内自由转动的轻杆，另一端与一小球相连，如图甲所示。现使小球在竖直平面内做圆周运动，到达某一位置开始计时，取水平向右为正方向，小球的水平分速度vx随时间t的变化关系如图乙所示，不计空气阻力，下列说法中正确的是（ ）
A．t1时刻小球通过最高点，t3时刻小球通过最低点
B．t2时刻小球通过最高点，t3时刻小球通过最低点
C．v1大小一定小于 v2大小，图乙中 S1和 S2的面积一定相等
D．v1大小可能等于 v2大小，图乙中 S1和 S2的面积可能不等
【解答】解：AB、由对称性可知，在最高点左右两侧对称位置，小球沿水平方向分速度相同，那么在小球到达最高点时，其前后对称时刻的小球水平分速度相等，且最高点时刻水平分速度为正，在图乙中t1时刻满足要求，所以t1时刻小球通过最高点，同理，t3时刻小球通过最低点，故A正确，B错误；
CD、从t2到t3，小球重力做正功，一直在加速，在最低点时，速度最大，沿水平方向分速度也最大，即v2＞v1，另外根据对称运动过程中分析，可知，S1和S2分别代表从最低点到最左边点以及从最左边点到最高点的水平位移大小，它们对称相等，因此S1和S2面积相等，故C正确，D错误；
故选：AC。
题型四 圆周运动中的两类临界问题
1．有些题目中有“刚好”、“恰好”、“正好”等字眼，明显表明题述的过程中存在着临界点．
2．若题目中有“取值范围”、“多长时间”、“多大距离”等词语，表明题述的过程中存在着“起止点”，而这些起止点往往就是临界点．
3．若题目中有“最大”、“最小”、“至多”、“至少”等字眼，表明题述的过程中存在着极值，这些极值点也往往是临界点．
（多选）如图所示，物体P用两根长度相等、不可伸长的细线系于竖直杆上，它随杆转动，若转动角速度为ω，则（ ）
A．ω只有超过某一值时，绳子AP才有拉力
B．绳子BP的拉力随ω 的增大而不变
C．绳子BP的张力一定大于绳子AP的张力
D．当ω增大到一定程度时，绳子AP的张力大于绳子BP的张力
【解答】解：设BP绳与竖直方向的夹角为θ，AP绳与竖直方向的夹角为α，对物体P进行受力分析，根据向心力公式则有：
TBPcsθ＝mg+TAPcsα…①
TBPsinθ+TAPsinα＝mω2r…②
A、当ω较小时，BP绳在水平方向的分量可以提供向心力，此时AP绳没有力，当ω增加到某值时，BP绳在水平方向的分量不足以提供向心力，此时绳子AP才有力的作用，故A正确；
B、ω的增大，所需的向心力增大，绳子BP的力增大。故B错误；
C、当AP绳子没有拉直时，AP绳拉力等于零，BP绳肯定有拉力，当AP绳拉直时，θ＝α，由①式可知，绳BP的张力一定大于绳子AP的张力，故C正确，D错误；
故选：AC。
（多选）汽车在出厂前要进行性能测试。某次测试中，测试人员驾驶着汽车在一个空旷的水平场地上沿直线以恒定的速度v0匀速行驶，突然发现正前方的道路出现故障，为了躲避故障，测试人员采取了一些应急措施。设汽车与路面间的滑动摩擦因数为μ，最大静摩擦力等于滑动摩擦力，重力加速度为g，则关于测试人员采取的应急措施说法正确的是（ ）
A．若直线刹车，则至少应该在道路故障前的距离处采取刹车
B．若以原有速率转弯，转弯半径越大，汽车受到的侧向摩擦力越大
C．若以原有速率转弯，转弯的最小半径为
D．以原速率转弯要比以直线刹车更安全一些
【解答】解：A、若直线刹车，刹车的加速度aμg，根据速度与位移关系知：x，则至少应该在道路故障前的距离处采取刹车，故A正确；
B、根据摩擦力充当向心力知f，若以原有速率转弯，转弯半径越大，汽车受到的侧向摩擦力越小，故B错误；
C、当f＝μmg时，根据f知半径最小为：R，故C正确；
D、由于Rx，以原速率转弯要比以直线刹车更危险，故D错误。
故选：AC。
（多选）如图所示，某同学用硬塑料管和一个质量为m的铁质螺丝帽研究匀速圆周运动，将螺丝帽套在塑料管上，手握塑料管使其保持竖直并在水平方向做半径为r的匀速圆周运动，则只要运动角速度合适，螺丝恰好不下滑，假设螺丝帽与塑料管间的动摩擦因数为μ，认为最大静摩擦力近似等于滑动摩擦力。则在该同学手转塑料管使螺丝帽恰好不下滑时，下列分析正确的是（ ）
A．螺丝帽的重力与其受到的最大静摩擦力平衡
B．螺丝帽受到塑料管的弹力方向水平向外，背离圆心
C．此时手转动塑料管的角速度
D．若塑料管的转动加快，螺丝帽不可能相对塑料管发生运动
【解答】解：A、螺丝帽受到竖直向下的重力、水平方向的弹力和竖直向上的最大静摩擦力，螺丝帽在竖直方向上没有加速度，所以螺丝帽的重力与最大静摩擦力平衡，故A正确；
B、螺丝帽做匀速圆周运动，由弹力提供向心力，所以弹力方向水平向里，指向圆心，故B错误；
C、对螺丝帽受力分析，根据牛顿第二定律得：N＝mω2r
竖直方向上，由平衡条件得：fm＝mg
又根据滑动摩擦力公式得：fm＝μN
联立解得：ω，故C正确；
D、若塑料管的转动加快，角速度ω增大，螺丝帽受到的弹力N增大，最大静摩擦力增大，螺丝帽不可能相对塑料管发生运动，故D正确。
故选：ACD。
如图1，用一根长为L＝1m的细线，一端系一质量为m＝1kg的小球（可视为质点），另一端固定在一光滑锥体顶端，锥面与竖直方向的夹角θ＝37°，当小球在水平面内绕锥体的轴做匀速圆周运动的角速度为ω时，细线的张力为T．求（g＝10m/s2，sin37°，cs37°，计算结果可用根式表示）：
（1）若要小球离开锥面，则小球的角速度ω0至少为多大？
（2）若细线与竖直方向的夹角为60°，则小球的角速度ω′为多大？
（3）细线的张力T与小球匀速转动的加速度ω有关，当ω的取值范围在0到ω′之间时，请通过计算求解T与ω2的关系，并在图2坐标纸上作出T﹣ω2的图象，标明关键点的坐标值。
【解答】解：（1）小球刚要离开锥面时的速度，此时支持力为零，根据牛顿第二定律得：
mgtanθ＝mωLsin θ
解得：ω0rad/s．
（2）同理，当细线与竖直方向成60°角时，由牛顿第二定律及向心力公式有：
mgtan α＝mω′2Lsin α
解得：ω′rad/s．
（3）a．当ω1＝0时 T1＝mgcsθ＝8N，标出第一个特殊点坐标（ 0，8N）；
b．当0＜ωrad/s时，根据牛顿第二定律得：
Tsinθ﹣Ncsθ＝mω2Lsinθ，
Tcsθ+Nsinθ＝mg
解得
当时，T2＝12.5N 标出第二个特殊点坐标[12.5（rad/s）2，12.5N]；
c．当时，小球离开锥面，设细线与竖直方向夹角为β，

解得：
当时，T3＝20N
标出第三个特殊点坐标[20（rad/s）2，20N]．
画出T﹣ω2图象如图所示．
答：
（1）若要小球离开锥面，则小球的角速度ω0至少为rad/s．
（2）若细线与竖直方向的夹角为60°，则小球的角速度ω′为2rad/s．
（3）T﹣ω2的图象如上所示．
绳模型
杆模型
常见类型
均是没有支撑的小球
均是有支撑的小球
过最高点的临界条件
由mg＝meq \f(v2,r)得
v临＝eq \r(gr)
由小球恰能做圆周运动得v临＝0
讨论分析
(1)过最高点时，v≥eq \r(gr)，FN＋mg＝meq \f(v2,r)，绳、圆轨道对球产生弹力FN
(2)不能过最高点时，v