备战高考2024年数学第一轮专题复习9.2 椭圆（精讲）（提升版）（解析版）

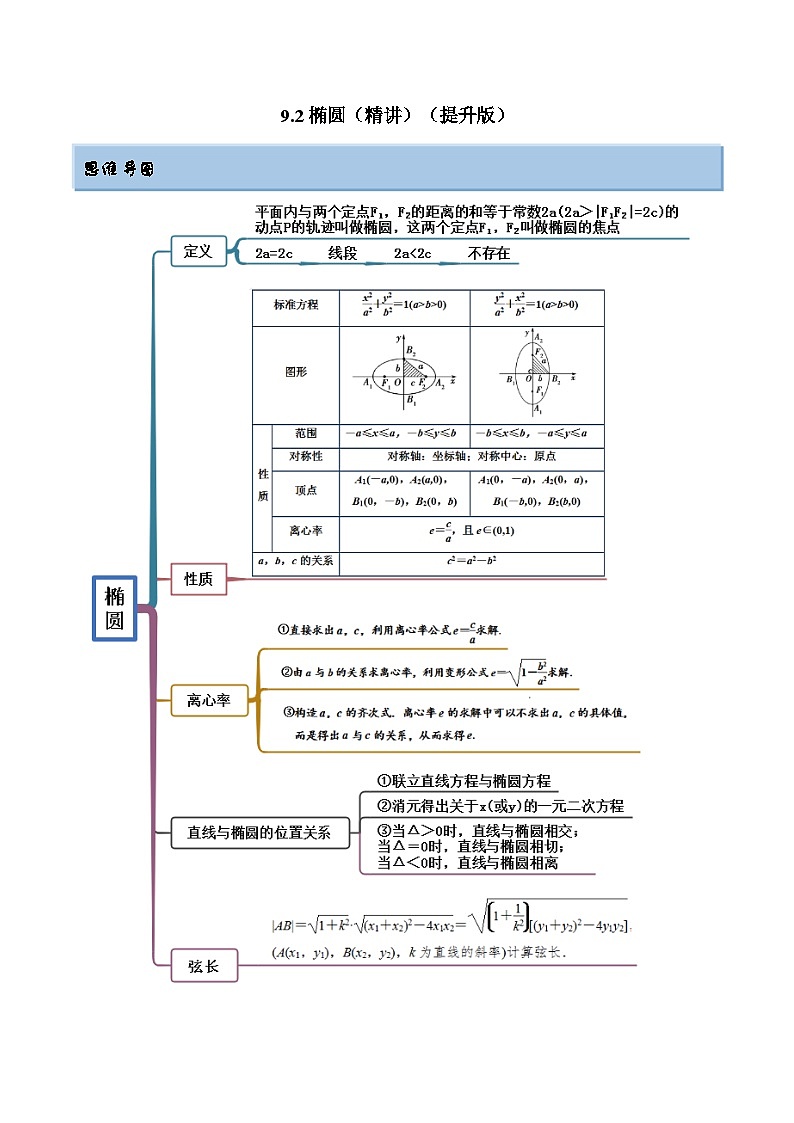
9.2 椭圆（精讲）（提升版）

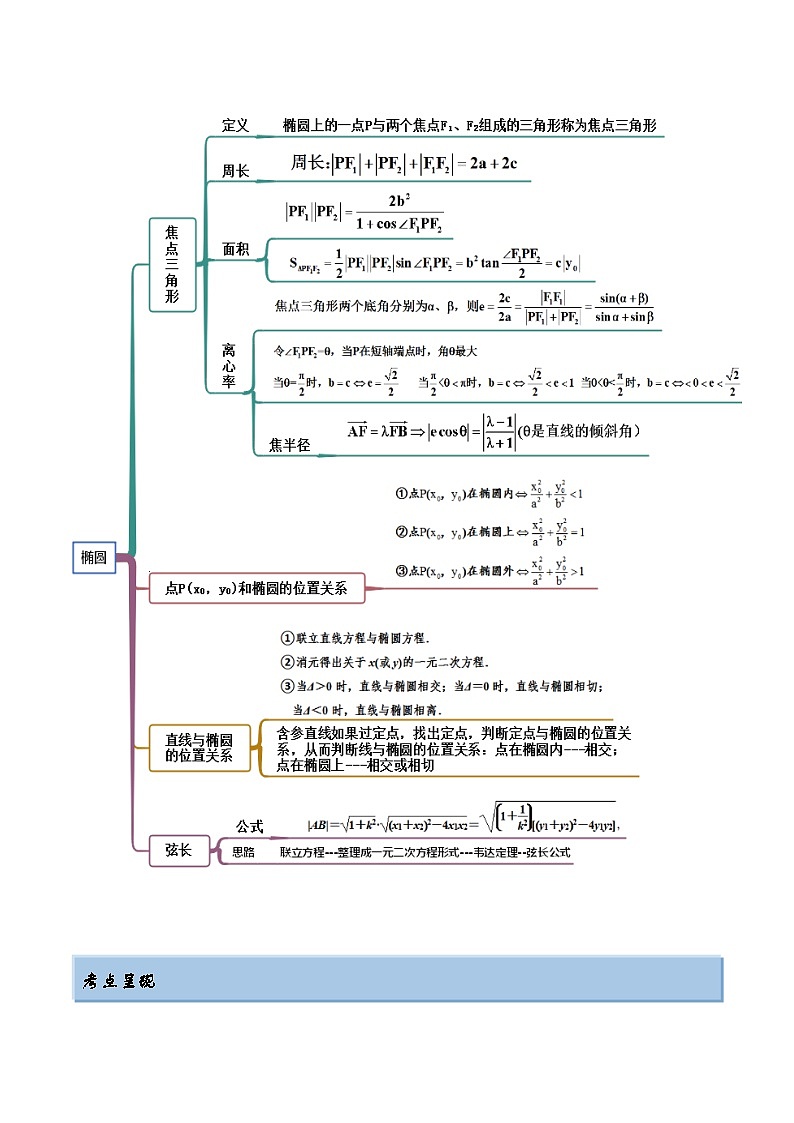
考点一 椭圆定义及应用

【例1-1】（2022·日照模拟）已知曲线 ，则“ ”是“曲线C是椭圆”的(　　) 

A．充要条件 B．充分不必要条件

C．必要不充分条件 D．既不充分也不必要条件

【答案】C

【解析】若曲线 表示椭圆，则 ，

故“ ”是“曲线C是椭圆”的必要不充分条件．故答案为：C．

【例1-2】（2022·江阴模拟）设是椭圆的左，右焦点，过的直接l交椭圆于A，B两点，则的最大值为（　　）

A．14 B．13 C．12 D．10

【答案】A

【解析】由椭圆的定义，知，，

所以的周长为，

所以当最小时，最大.又当时，最小，此时，所以的最大值为.故答案为：A.

【例1-3】（2021高三上·桂林月考）点P是椭圆 上的点， 、 是椭圆的左、右焦点，则△ 的周长是（　　） 

A．12 B．10 C．8 D．6

【答案】B

【解析】点P是椭圆 上的点， 、 是椭圆的左、右焦点，

其中 由抛物线定义得： .

△ 的周长为 .故答案为：B.

【一隅三反】

1．（2022·江西模拟）“”是“方程表示椭圆”的（　　）

A．充分不必要条件 B．必要不充分杂件

C．充要杂件 D．既不充分也不必要条件

【答案】D

【解析】由，可得，

当时，方程可化为，此时方程表示圆，所以充分性不成立；

反之：方程表示椭圆，则满足，即且，

所以不成立，即必要性不成立，所以“”是“方程表示椭圆”的既不充分也不必要条件.故答案为：D.

2．（2022·江西模拟）“ ， ”是“方程 表示的曲线为椭圆”的（　　） 

A．充要条件 B．必要不充分条件

C．充分不必要条件 D．既不充分也不必要条件

【答案】D

【解析】[解法一]

方程 即方程 ，表示椭圆的充分必要条件是 ，

显然“ ， ”是“ ”既不充分也不必要条件，

故“ ， ”是“方程 表示的曲线为椭圆”的既不充分也不必要条件，

[解法二]

当 时，满足“ ， ”，此时题中方程可化为： ，表示的曲线是圆而不是椭圆，当 时，不满足“ ， ”，只是题中方程可化为： ，表示中心在原点，半长轴为1，半短轴为 的椭圆，

故：“ ， ”是“方程 表示的曲线为椭圆”的既不充分也不必要条件，

故答案为：D

3．（2021高三上·珠海月考）已知点 ，且 是椭圆 的左焦点， 是椭圆上任意一点，则 的最小值是（　　） 

A．6 B．5 C．4 D．3

【答案】D

【解析】 ， 设椭圆的右焦点为 ，

，

当 在 的正上方时，等号成立.故答案为：D

考点二 椭圆的标准方程

【例2】（2021高三上·信阳开学考）已知椭圆 的左、右焦点分别是 ，焦距 ，过点 的直线与椭圆交于P、Q两点，若 ，且 ，则椭圆C的方程为(　　) 

A． B． C． D．

【答案】A

【解析】如图， ，则 ，

延长 交椭圆C于点M，得 ，
设 ，则 ，据椭圆的定义有 ，在 中， 得 ，
又在 中， 得
故 ，则椭圆C的方程为 .故答案为：A

【一隅三反】

1．（2022·内江模拟）以椭圆 的短轴的一个端点和两焦点为顶点的三角形为等边三角形，且椭圆 上的点到左焦点的最大距离为6，则椭圆 的标准方程为（　　） 

A． B． C． D．

【答案】C

【解析】由题意知：短轴端点与焦点形成等边三角形，则 ，
椭圆上的点到左焦点最大距离为6，即 ，则 ， ， .

则椭圆的标准方程为： .故答案为：C.

2．（2021·全国高三专题练习）阿基米德是古希腊著名的数学家､物理学家，他利用“逼近法”得到椭圆的面积除以圆周率等于椭圆的长半轴长与短半轴长的乘积，已知在平面直角坐标系中，椭圆的面积为，两焦点与短轴的一个端点构成等边三角形，则椭圆的标准方程是（    ）

A． B． C． D．

【答案】A

【解析】由题意得，解得，

所以椭圆的标准方程是.

故选：A

3．（2021·山西长治市·高三月考（文））古希腊数学家阿波罗尼奥斯采用平面切割圆锥的方法来研究圆锥曲线，用垂直于圆锥轴的平面去截圆锥，得到的截面是圆；把平面再渐渐倾斜得到的截面是椭圆.若用周长为72的矩形ABCD截某圆锥得到椭圆τ，且τ与矩形ABCD的四边相切.设椭圆τ在平面直角坐标系中的方程为，下列选项中满足题意的方程为（    ）

A． B．

C． D．

【答案】C

【解析】由题意椭圆方程是方程为，排除BD，

矩形的四边与椭圆相切，则矩形的周长为，．

在椭圆中，，, 不满足题意，

在椭圆中，, 满足题意．

故选：C．

考点三 椭圆的离心率

【例3-1】（2022·秦皇岛二模）椭圆的左､右焦点分别为，，为椭圆上一点，若的周长为，则椭圆的离心率为（　　）

A． B． C． D．

【答案】B

【解析】因为，所以.

因为的周长为，所以，所以，

所以椭圆的离心率为，故答案为：B.

【例3-2】（2022·浙江模拟）已知椭圆以为左右焦点，点P、Q在椭圆上，且过右焦点，，若，则该椭圆离心率是（　　）

A． B． C． D．

【答案】A

【解析】根据题意可得如图椭圆，

是直角三角形，，

不妨设，则，

因为，

所以，

，

所以离心率．

故答案为：A．

【例3-3】（2022·南充模拟）已知P为椭圆上任意一点，点M，N分别在直线与上，且，，若为定值，则椭圆的离心率为（　　）

A． B． C． D．

【答案】D

【解析】设，，则直线的方程为，

直线的方程为，

联立方程组，解得，，

联立方程组，解得，，

，

，在椭圆上，，

为定值，

，．

．故答案为：D.

【一隅三反】

1．（2022·湘潭三模）椭圆的左､右焦点分别为F1，F2，过点F1的直线l与E交于A，B两点，若△ABF2的周长为12，则E的离心率为（　　）

A． B． C． D．

【答案】A

【解析】因为的周长为12，根据椭圆的定义可得，解得，

则，所以，则椭圆的离心率为.故答案为：A.

2．（2022·安康模拟）以椭圆的左､右顶点作为双曲线的左､右焦点，以的焦点作为的顶点，则的离心率为（　　）

A． B． C．2 D．

【答案】C

【解析】由题可知的焦距为4，实轴长为，所以的离心率为

故答案为：C

3．（2022·福建模拟）已知点、分别是椭圆的左、右焦点，过的直线交椭圆于、两点，且满足，，则该椭圆的离心率是（　　）

A． B． C． D．

【答案】B

【解析】如下图所示：

设，则，因为，则，

由椭圆的定义可得，则，

所以，，则，

由勾股定理可得，则，则，

因此，该椭圆的离心率为。

故答案为：B.

4．（2021高三上·金台月考）已知椭圆，F1，F2分别为椭圆的左、右焦点，若椭圆上存在一点P，使得，则该椭圆离心率的取值范围为（　　）

A． B． C． D．

【答案】D

【解析】所以，又，所以，

，故答案为：D．

5．（2021·蚌埠模拟）已知椭圆 的右顶点为 ，坐标原点为 ，若椭圆上存在一点 使得 是等腰直角三角形，则该椭圆的离心率为（　　） 

A． B． C． D．

【答案】C

【解析】由题意知，可设点P，代入 得，解得a2=3b2，
则c2=2b2，则离心率为 故答案为：C

考点四 直线与椭圆的位置关系

【例4-1】（2023·全国·高三专题练习）直线与椭圆的位置关系是（       ）

A．相交 B．相切 C．相离 D．不确定

【答案】A

【解析】，在椭圆内，

恒过点，直线与椭圆相交.故选：A.

【例4-2】（2023·全国·高三专题练习）已知椭圆的左､右焦点分别为､，过且斜率为的直线与椭圆交于，两点，若为钝角，则的取值范围为（       ）

A． B．

C． D．

【答案】D

【解析】设直线方程为，

联立方程组得，

则.

因为为钝角，所以.

因为

，所以.

因为当时，三点共线，不符合题意，所以.

故答案为：D

【一隅三反】

1．（2021·辽宁）已知直线l：，曲线C：，则直线l与曲线C的位置关系是（       ）

A．相离 B．相切 C．相交 D．无法确定

【答案】C

【解析】由直线l：，得直线l过定点，

因为，所以该点在曲线C：内部.所以直线l与曲线C相交.故选：C.

2．（2022·全国·高二课时练习）直线与椭圆有且只有一个交点，则的值是(       )

A． B． C． D．

【答案】C

【解析】由得，，

由题意知，解得，

故选：C．

3．（2022·贵州贵阳·高三开学考试（理））已知椭圆的离心率是，点在椭圆 上．

(1)求椭圆的标准方程；

(2)过点的直线与椭圆交于两点， 求为坐标原点)面积的最大值．

【答案】(1)；

(2).

【解析】（1）由题意可得 ，解得，故椭圆C的标准方程为；

（2）由题意可知直线的斜率存在，

设直线 ，

联立 ，整理得 ，

，

所以， 即 或，

则 ，

故 ，

点到直线的距离，

则的面积，

设，则 ，

故 ， 当且仅当时，等号成立，

即面积的最大值为．

考点五 弦长及中点弦

【例5-1】（2022·吉林省实验中学）已知斜率为1的直线l过椭圆的右焦点，交椭圆于A，B两点，则弦AB的长为（       ）

A． B． C． D．

【答案】C

【解析】由椭圆知，，所以，

所以右焦点坐标为，则直线的方程为，

设，

联立，消y得，，

则，

所以.

即弦AB长为.

故选：C.

【例5-2】（2023·全国·高三专题练习）已知椭圆，则以点为中点的弦所在的直线方程为（　　）

A． B．

C． D．

【答案】C

【解析】设弦的两个端点分别为，，

则，

①﹣②得：，

即，

所以．

故以点为中点的弦所在的直线方程为y，

整理得：.

故选：C.

【例5-3】（2022·全国·高三专题练习）过椭圆：右焦点的直线：交于，两点，为的中点，且的斜率为，则椭圆的方程为（       ）

A． B．

C． D．

【答案】A

【解析】依题意，焦点，即椭圆C的半焦距，设，，

则有，两式相减得：，

而，且，即有，

又直线的斜率，因此有，而，解得，经验证符合题意，

所以椭圆的方程为.

故选：A

【一隅三反】

1．（2022广东）椭圆中，以点为中点的弦所在直线的斜率为（       ）

A． B． C． D．

【答案】C

【解析】代入椭圆得，

两式相减得，

即，

即，又

即，

即，

∴弦所在的直线的斜率为，

故选：C.

2．（2022·全国·高三专题练习）已知双曲线C的中心在坐标原点，焦点在x轴上，离心率等于，点在双曲线C上，椭圆E的焦点与双曲线C的焦点相同，斜率为的直线与椭圆E交于A、B两点．若线段AB的中点坐标为，则椭圆E的方程为（       ）

A． B．

C． D．

【答案】D

【解析】设双曲线方程为，则，解得，故双曲线方程为，焦点为；

设椭圆方程为，则椭圆焦点为焦点为，故，设，则，

两式相减得，整理得，即，解得，故，椭圆方程为.

故选：D.

3．（2022·安徽）已知椭圆的右焦点与抛物线的焦点重合，过点的直线交于、两点， 若的中点坐标为，则的方程为（       ）

A． B．

C． D．

【答案】D

【解析】设、，若轴，则、关于轴对称，不合乎题意，

将、的坐标代入椭圆方程得，两式相减得，

可得，

因为线段的中点坐标为，所以，，，

因为抛物线的焦点为，所以，

又直线过点，因此，所以，，

整理得，又，解得，，

因此，椭圆的方程为，

故选：D.

4．（2022·全国·高三专题练习）椭圆的左、右顶点分别为、，点在上，且直线的斜率为，则直线斜率为（       ）

A． B．3 C． D．

【答案】B

【解析】椭圆的左、右顶点分别为、，

点坐标为，点坐标为，

又直线的斜率为，

直线的方程为：，

代入椭圆方程可得：，

设点坐标为，则，解得，，

故直线斜率，

故选:B．