2024年高考数学第一轮复习专题08 幂函数与二次函数（解析版）

这是一份2024年高考数学第一轮复习专题08 幂函数与二次函数（解析版），共26页。
题型一：幂函数的定义及其图像
题型二：幂函数性质的综合应用
题型三：二次方程的实根分布及条件
题型四：二次函数“动轴定区间”、“定轴动区间”问题
【考点预测】
1、幂函数的定义
一般地，（为有理数）的函数，即以底数为自变量，幂为因变量，指数为常数的函数称为幂函数．
2、幂函数的特征：同时满足一下三个条件才是幂函数
①的系数为1；②的底数是自变量；③指数为常数．
（3）幂函数的图象和性质
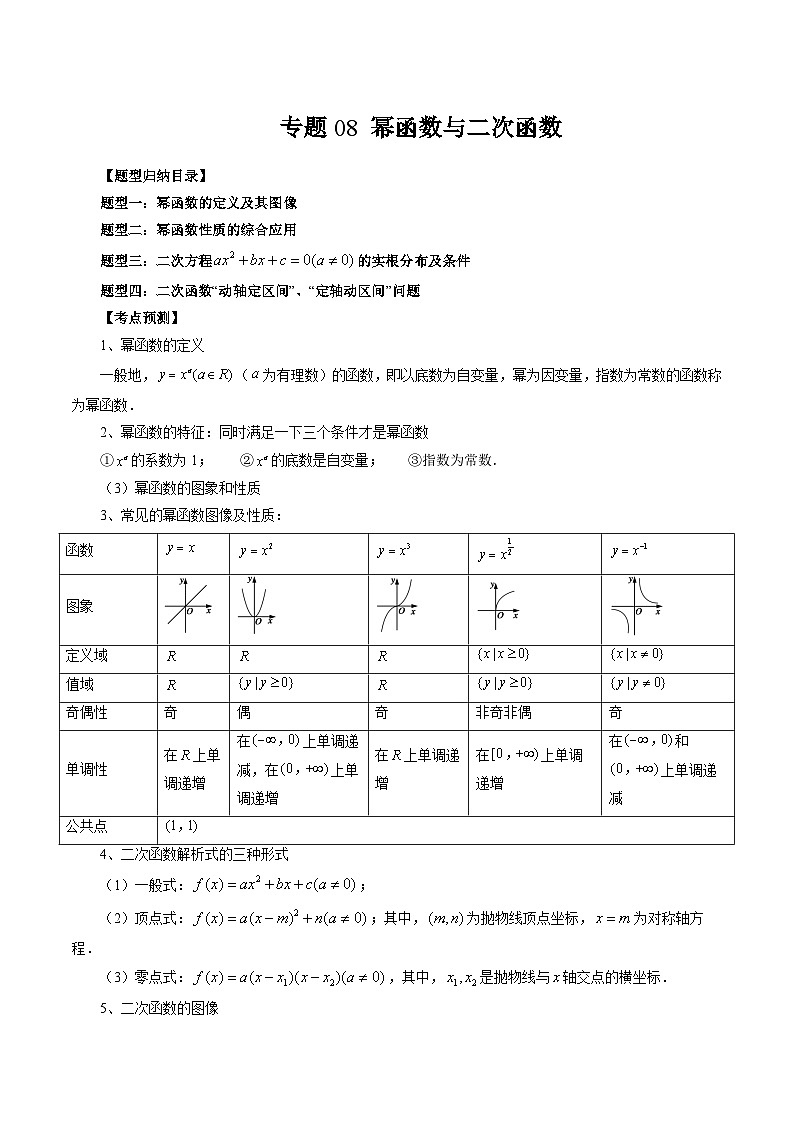
3、常见的幂函数图像及性质：
4、二次函数解析式的三种形式
（1）一般式：；
（2）顶点式：；其中，为抛物线顶点坐标，为对称轴方程．
（3）零点式：，其中，是抛物线与轴交点的横坐标．
5、二次函数的图像
二次函数的图像是一条抛物线，对称轴方程为，顶点坐标为．
（1）单调性与最值
O
图2-9
O
图2-8
= 1 \* GB3 ①当时，如图所示，抛物线开口向上，函数在上递减，在上递增，当时，； = 2 \* GB3 ②当时，如图所示，抛物线开口向下，函数在上递增，在上递减，当时，；．
（2）与轴相交的弦长
当时，二次函数的图像与轴有两个交点和，．
6、二次函数在闭区间上的最值
闭区间上二次函数最值的取得一定是在区间端点或顶点处．
对二次函数，当时，在区间上的最大值是，最小值是，令：
（1）若，则；
（2）若，则；
（3）若，则；
（4）若，则．
【方法技巧与总结】
1、幂函数在第一象限内图象的画法如下：
①当时，其图象可类似画出；
②当时，其图象可类似画出；
③当时，其图象可类似画出．
2、实系数一元二次方程的实根符号与系数之间的关系
（1）方程有两个不等正根
（2）方程有两个不等负根
（3）方程有一正根和一负根，设两根为
3、一元二次方程的根的分布问题
一般情况下需要从以下4个方面考虑：
（1）开口方向；（2）判别式；（3）对称轴与区间端点的关系；（4）区间端点函数值的正负．
设为实系数方程的两根，则一元二次的根的分布与其限定条件如表所示．
4、有关二次函数的问题，关键是利用图像．
（1）要熟练掌握二次函数在某区间上的最值或值域的求法，特别是含参数的两类问题——动轴定区间和定轴动区间，解法是抓住“三点一轴”，三点指的是区间两个端点和区间中点，一轴指对称轴．即注意对对称轴与区间的不同位置关系加以分类讨论，往往分成： = 1 \* GB3 ①轴处在区间的左侧； = 2 \* GB3 ②轴处在区间的右侧； = 3 \* GB3 ③轴穿过区间内部（部分题目还需讨论轴与区间中点的位置关系），从而对参数值的范围进行讨论．
（2）对于二次方程实根分布问题，要抓住四点，即开口方向、判别式、对称轴位置及区间端点函数值正负．
【典例例题】
题型一：幂函数的定义及其图像
【方法技巧与总结】
确定幂函数的定义域，当为分数时，可转化为根式考虑，是否为偶次根式，或为则被开方式非负．当时，底数是非零的．
例1．（2023·全国·高三专题练习）已知为幂函数， 且， 则（ ）
A．B．C．D．
【答案】B
【解析】因为为幂函数，
设，则，
所以，可得，则.
故选：B
例2．（2023·全国·高三专题练习）当时，幂函数为减函数，则实数m的值为（ ）
A．B．
C．或D．
【答案】A
【解析】因为函数既是幂函数又是的减函数，
所以解得：.
故选：A.
例3．（2023·全国·高三专题练习）现有下列函数：①；②；③；④；⑤；⑥；⑦，其中幂函数的个数为（ ）
A．1B．2C．3D．4
【答案】B
【解析】幂函数满足形式，故，满足条件，共2个
故选：B
变式1．（2023·全国·高三专题练习）幂函数在上为增函数，则实数的值为（ ）
A．B．0或2C．0D．2
【答案】D
【解析】因为是幂函数，所以，解得或，
当时，在上为减函数，不符合题意，
当时，在上为增函数，符合题意，
所以.
故选：D.
变式2．（2023·全国·高三专题练习）幂函数y＝（m∈Z）的图象如图所示，则实数m的值为________.
【答案】1
【解析】有图象可知：该幂函数在单调递减，所以，解得，,故可取，又因为该函数为偶函数，所以为偶数，故
故答案为：
题型二：幂函数性质的综合应用
【方法技巧与总结】
紧扣幂函数的定义、图像、性质，特别注意它的单调性在不等式中的作用，这里注意为奇数时，为奇函数，为偶数时，为偶函数．
例4．（2023·全国·高三专题练习）设，则使函数的定义域为，且该函数为奇函数的值为（ ）
A．或B．或C．或D．、或
【答案】A
【解析】因为定义域为，所以，，
又函数为奇函数，所以，则满足条件的或.
故选:A
例5．（2023·全国·高三专题练习）下列函数中，定义域与值域均为R的是（ ）
A．B．C．D．
【答案】C
【解析】A. 函数的定义域为，值域为R；
B. 函数的定义域为R，值域为；
C. 函数的定义域为R，值域为R；
D. 函数的定义域为，值域为，
故选：C
例6．（2023·全国·高三专题练习）已知幂函数的图像过点，则 的值域是（ ）
A．B．
C．D．
【答案】D
【解析】幂函数的图像过点，
，解得，
，
的值域是.
故选：D.
变式3．（2023·全国·高三专题练习）已知幂函数的图像关于y轴对称．
(1)求的解析式；
(2)求函数在上的值域．
【解析】（1）因为是幂函数，
所以，解得或．
又的图像关于y轴对称，所以，
故．
（2）由（1）可知，．
因为，所以，
又函数在上单调递减，在上单调递增，
所以．
故在上的值域为．
变式4．（多选题）（2023·全国·高三专题练习）下列结论中正确的是（ ）
A．幂函数的图像都经过点，
B．幂函数的图像不经过第四象限
C．当指数取1，3，时，幂函数是增函数
D．当时，幂函数在其整个定义域上是减函数
【答案】BC
【解析】A选项，当指数时，幂函数的图像不经过原点，故A错误；
B选项，所有的幂函数在区间上都有定义且，所以幂函数的图像不可能经过第四象限，故B正确；
C选项，当α为1，3，时，是增函数，显然C正确；
D选项，当时，在区间和上是减函数，但在整个定义域上不是减函数，故D错误.
故选：BC
变式5．（2023·上海·高三专题练习）已知，若幂函数为奇函数，且在上是严格减函数，则取值的集合是______．
【答案】
【解析】∵，
幂函数为奇函数，且在上递减，
∴是奇数，且，∴．
故答案为：
变式6．（2023·全国·高三专题练习）函数是幂函数，对任意，，且，满足，若，，且，则的值：
①恒大于0；②恒小于0；③等于0；④无法判断．
上述结论正确的是__（填序号）．
【答案】①
【解析】由于函数是幂函数，故，解得或．
由于对任意的，，且，满足，所以函数在上为增函数，
当时，符合题意，
当时，不符合题意，
故，且函数为奇函数．
由于，，且，
所以，由于函数为单调递增函数和奇函数，故，
所以，
所以，
故答案为：①
变式7．（2023·全国·高三专题练习）已知幂函数为奇函数，且在上单调递减，则_______．
【答案】
【解析】因为幂函数为奇函数，
所以或1或3，
又因为幂函数在上单调递减，
所以，
故答案为：.
题型三：二次方程的实根分布及条件
【方法技巧与总结】
结合二次函数的图像分析实根分布，得到其限定条件，列出关于参数的不等式，从而解不等式求参数的范围．
例7．（2023·全国·高三专题练习）已知方程的两根分别在区间，之内，则实数的取值范围为______．
【答案】.
【解析】方程
方程两根为，
若要满足题意，则，解得，
故答案为：.
例8．（2023·全国·高三专题练习）若关于x的方程的一根大于－1，另一根小于－1，则实数k的取值范围为______．
【答案】
【解析】由题意，关于的方程的一根大于-1，另一根小于-1，
设，根据二次函数的性质，可得，解得，
所以实数的取值范围为.
故答案为：.
例9．（2023·全国·高三专题练习）已知一元二次方程x2＋ax＋1＝0的一个根在(0，1)内，另一个根在(1，2)内，则实数a的取值范围为________．
【答案】
【解析】设f (x)＝x2＋ax＋1，由题意知，解得－