

浙教版八年级上册数学第1章三角形的初步知识(A卷)含解析答案
展开第1章 三角形的初步知识(A卷)
学校:___________姓名:___________班级:___________考号:___________
| 一、单选题 |
1.化简的值是( )
A.1 B. C.2020 D.
2.下列说法中,正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
3.在古代,人们通过在绳子上打结来计数.即“结绳计数”.当时有位父亲为了准确记录孩子的出生天数,在粗细不同的绳子上打结(如图),由细到粗(右细左粗),满七进一,那么孩子已经出生了( )
A.1335天 B.516天 C.435天 D.54天
4.若,则称是以10为底的对数.记作:.例如:,则;,则.对数运算满足:当,时,,例如:,则的值为( )
A.5 B.2 C.1 D.0
5.下列各组数中,不相等的是( )
A.与 B.与 C.与 D.与
6.阅读理解:如果一个正整数m能表示为两个正整数a,b的平方和,即,那么称m为广义勾股数.则下面的四个结论:①7不是广义勾股数;②13是广义勾股数;③两个广义勾股数的和是广义勾股数;④两个广义勾股数的积是广义勾股数.依次正确的是( )
A.②④ B.①②④ C.①② D.①④
7.观察下列算式:,,,,….根据上述算式中的规律,请你猜想的末尾数字是( )
A.2 B.4 C.8 D.6
8.定义运算:若,则,例如,则.运用以上定义,计算:( )
A. B.2 C.1 D.4
9.观察下列算式:,,,,,,,,…,,,,,,,,,…,根据上述算式中的规律,的末位数字是( )
A.3 B.5 C.7 D.9
10.计算 (m个9)=( )
A.81 B.9m C. D.
| 二、填空题 |
11.已知,则 .
12.已知,都是实数,若,则 .
13.《庄子》中记载:“一尺之棰,日取其半,万世不竭.”这句话的意思是一尺长的木棍,每天截取它的一半,永远也截不完,若按此方式截一根长为1的木棍,第4天截取后木棍剩余的长度是 .
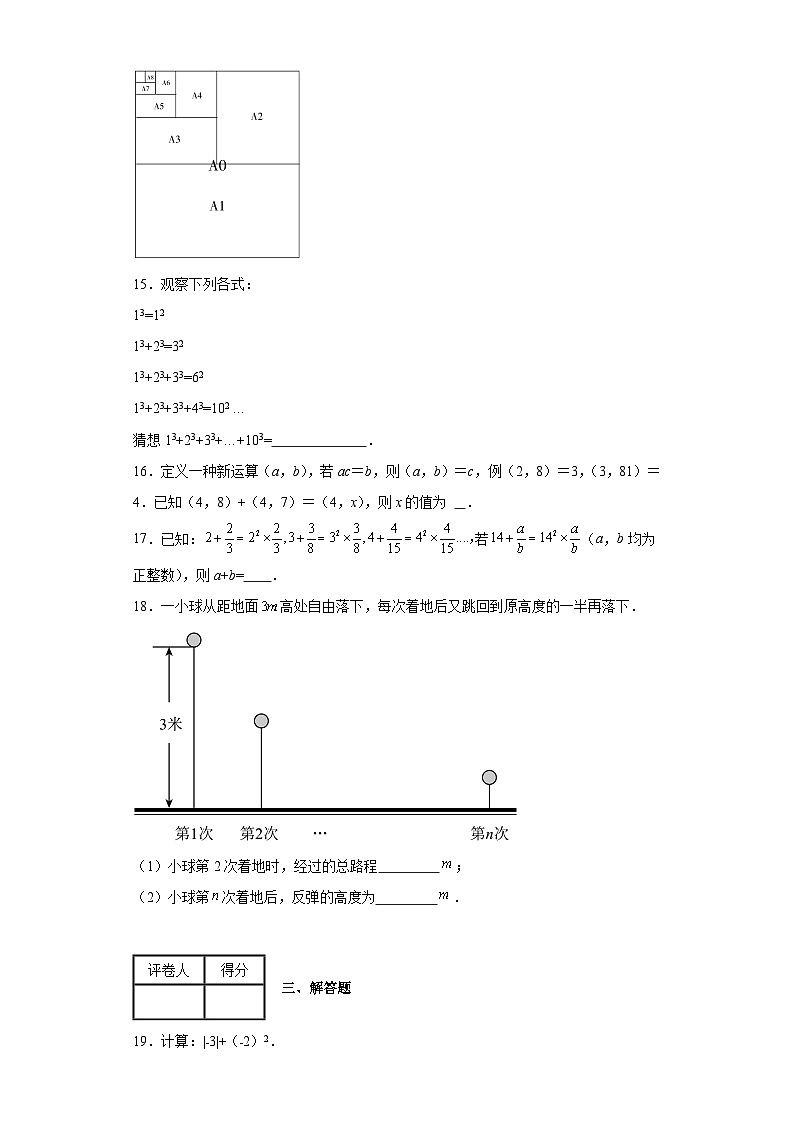
14.如图是各大小型号的纸张长宽关系裁剪对比图,可以看出纸张大小的变化规律:A0纸长度方向对折一半后变为A1纸;A1纸长度方向对折一半后变为A2纸;A2纸长度方向对折一半后变为A3纸;A3纸长度方向对折一半后变为A4纸……A4规格的纸是我们日常生活中最常见的,那么有一张A4的纸可以裁 张A8的纸.
15.观察下列各式:
13=12
13+23=32
13+23+33=62
13+23+33+43=102 …
猜想13+23+33+…+103= .
16.定义一种新运算(a,b),若ac=b,则(a,b)=c,例(2,8)=3,(3,81)=4.已知(4,8)+(4,7)=(4,x),则x的值为 .
17.已知:若(a,b均为正整数),则a+b= .
18.一小球从距地面高处自由落下,每次着地后又跳回到原高度的一半再落下.
(1)小球第2次着地时,经过的总路程 ;
(2)小球第次着地后,反弹的高度为 .
| 三、解答题 |
19.计算:|﹣3|+(﹣2)2.
20.计算:
21.把下列各数在数轴上表示出来,再用“<”号连接起来.
22.自年月以来,甲流便肆虐横行,成为当前主流流行疾病.某一小区有位住户不小心感染了甲流,由于甲流传播感染非常快,小区经过两轮传染后共有人患了甲流.
(1)每轮感染中平均一个人传染几人?
(2)如果按照这样的传播速度,经过三轮传染后累计是否超过人患了甲流?
23.阅读材料:求1+2+22+23+24+…+22013的值.
解:设S=1+2+22+23+24+…+22012+22013,将等式两边同时乘以2得:
2S=2+22+23+24+25+…+22013+22014
将下式减去上式得2S﹣S=22014﹣1
即S=22014﹣1
即1+2+22+23+24+…+22013=22014﹣1
请你仿照此法计算:
(1)1+2+22+23+24+…+210
(2)1+3+32+33+34+…+3n(其中n为正整数).
24.数学不仅是一门学科,也是一种文化,即数学文化.数学文化包括数学史、数学美和数学应用等多方面.古时候,在某个王国里有一位聪明的大臣,他发明了国际象棋,献给了国王,国王从此迷上了下棋,为了对聪明的大臣表示感谢,国王答应满足这位大臣的一个要求.大臣说:“就在这个棋盘上放一些米粒吧.第格放粒米,第格放粒米,第格放粒米,然后是粒、粒、粒······一只到第格.”“你真傻!就要这么一点米粒?”国王哈哈大笑.大臣说:“就怕您的国库里没有这么多米!”国王的国库里真没有这么多米吗?题中问题就是求是多少?请同学们阅读以下解答过程就知道答案了.
设,
则
即:
事实上,按照这位大臣的要求,放满一个棋盘上的个格子需要粒米.那么到底多大呢?借助计算机中的计算器进行计算,可知答案是一个位数: ,这是一个非常大的数,所以国王是不能满足大臣的要求.请用你学到的方法解决以下问题:
我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座层塔共挂了盏灯,且相邻两层中的下一层灯数是上一层灯数的倍,则塔的顶层共有多少盏灯?
计算:
某中学“数学社团”开发了一款应用软件,推出了“解数学题获取软件激活码”的活动.这款软件的激活码为下面数学问题的答案:
已知一列数:,其中第一项是,接下来的两项是,再接下来的三项是,以此类推,求满足如下条件的所有正整数,且这一数列前项和为的正整数幂.请直接写出所有满足条件的软件激活码正整数的值.
参考答案:
1.A
【分析】根据有理数乘方的意义计算.
【详解】(-1)2020=1.
故选:A.
【点睛】考查了有理数的乘方,解题关键是-1的偶次方为正数,奇次方为负数.
2.B
【分析】根据绝对值的意义和乘方的性质,即可一一判定.
【详解】解:A.若,则不一定不等于,如,,故该说法错误,不符合题意;
B.若,则a为正数,且绝对值大,故,故该说法正确,符合题意;
C.若,则或,故该说法错误,不符合题意;
D.若,则a不一定大于b,如,,故该说法错误,不符合题意;
故选:B.
【点睛】本题考查了根据绝对值的意义和乘方的性质,关键是熟练掌握和运用绝对值的性质.
3.B
【分析】根据题意以及图形分析,根据满七进一,即可求解.
【详解】解:绳结表示的数为
故选B
【点睛】本题考查了有理数的混合运算,理解“满七进一”是解题的关键.
4.C
【分析】通过阅读自定义运算规则:,再得到 再通过提取公因式后逐步进行运算即可得到答案.
【详解】解: ,
故选C
【点睛】本题考查的是自定义运算,理解题意,弄懂自定义的运算法则是解本题的关键.
5.C
【分析】利用有理数乘方的运算逐项判断即可.
【详解】解:、,,∴与相等,故本选项错误,排除;
、,,∴与相等,故本选项错误;
、,,∴与不相等,故本选项正确;
、,,∴与相等,故本选项错误.
故选:.
【点睛】此题考查了乘方和绝对值的意义,解题的关键是熟练掌握有理数乘方的法则:奇负偶正.
6.C
【分析】结合题意,根据有理数乘方、有理数加法的性质计算,即可得到答案.
【详解】∵或或
∴7不是广义勾股数,即①正确;
∵
∴13是广义勾股数,即②正确;
∵,,不是广义勾股数
∴③错误;
设
则
当ad=bc或ac=bd时,两个广义勾股数的积不—定是广义勾股数,如2和2都是广义勾股数,但2×2=4,4不是广义勾股数,故④结论错误;
故①②正确
故选:C.
【点睛】本题考查了有理数运算的知识;解题的关键是熟练掌握有理数乘方、有理数加法的性质,从而完成求解.
7.B
【详解】分析:本题需先根据已知条件,找出题中的规律,即可求出210的末位数字.
解答:解:∵21=2,22=4,23=8,24=16,
25=32,26=64,27=128,28=256,…
∴210的末位数字是4.
故选B.
8.A
【分析】先根据乘方确定,根据新定义求出,然后代入计算即可.
【详解】解:∵,
∴
∴,
,
.
故选:A.
【点睛】本题考查新定义对数函数运算、乘方的逆运算等知识点,仔细阅读题目中的定义,找出新定义运算的实质是乘方的逆运算是解答本题的关键.
9.D
【分析】通过观察所给的式子,发现每次运算尾数循环出现,由此求解即可.
【详解】解:∵,,,,,,,,…,
∴其结果的末位数字每次运算尾数循环出现,
∵,
∴的末尾数字与的尾数相同为,
∵,,,,,,,,…,
∴其结果的末位数字每次运算尾数循环出现,
∵
∴的末尾数字与的尾数相同为,
∴的末位数字是:.
故选:D.
【点睛】本题考查数字的变化规律,通过观察所给的数的尾数,找到尾数循环出现的规律是解题的关键.
10.D
【分析】根据9+9+9+…+9=9m,,代入化简计算即可.
【详解】∵==,
故选D.
【点睛】本题考查了乘方运算,积的意义,熟练进行运算是解题的关键.
11.2
【分析】把4写成即可求出m的值.
【详解】解:∵且,
∴,
∴,
故答案为:2.
【点睛】本题主要考查了乘方的意义,正确把4写成是解答本题的关键.
12.
【分析】根据绝对值,偶次幂的非负性求出,,再代入计算即可.
【详解】∵,
∴,,
即,,
∴,
故答案为:.
【点睛】本题主要考查了绝对值,偶次幂的非负性,求出,的值是解本题的关键.
13.
【分析】根据题意依次每一天剩余木棍的长度,即可求得第4天截取后木棍剩余的长度.
【详解】解:第一天截取后剩:(米);
第二天截取后剩:(米);
第三天截取后剩:(米);
第四天截取后剩:(米);
故答案为:.
【点睛】本题考查了有理数乘方,掌握有理数乘方的意义及性质,理解题意写出算式是解题关键.
14.16
【分析】根据题意求出A4纸长度方向对折一半后变为A5纸,A5纸长度方向对折一半后变为A6纸……随之即可解答.
【详解】解:由题可知:
一张A4纸可以裁2张A5纸,
一张A5纸可以裁2张A6纸,
一张A6纸可以裁2张A7纸,
一张A7纸可以裁2张A8纸,
所以一张A4纸可以裁张A8纸,即16张.
【点睛】本题考查幂的运算,能够读懂题意列出式子是解答本题的关键.
15.552
【分析】由题意得出13+23+…+103=(1+2+…+10)2=552,即可得出答案;
【详解】解:∵13=12;
13+23= (1+2)2=32;
13+23+33=(1+2+3)2=62;
13+23+33+43=(1+2+3+4) 2=102
…
∴13+23+…+103=(1+2+…+10)2=552,
故答案为:552;
【点睛】本题考查了数字的变化规律和有理数的混合运算,根据题意数字变化规律是解题的关键.
16.56
【分析】设4m=8,4n=7,根据新运算可得m+n=(4,x),从而得到4m+n=x,即可求解.
【详解】解:设4m=8,4n=7,
∵(4,8)+(4,7)=(4,x),
∴m+n=(4,x),
∴4m+n=x,
∴4m×4n=x,
∴8×7=x,
∴x=56,
故答案为:56.
【点睛】本题考查有理数的混合运算、新定义,解答本题的关键是明确题意,会用新定义解答问题.
17.209
【分析】根据所给算式可知,,据此求解即可.
【详解】解:∵
∴,
∴,
∵,
∴a=14,b=142-1,
∴a+b=14+142-1=209.
故答案为:209.
【点睛】本题考查了规律型---数字类规律与探究,要求学生通过观察,分析、归纳发现其中的规律,并应用发现的规律解决问题.
18. 6
【分析】(1)根据题意可以求得小球第2次着地时,经过的总路程;
(2)逐一列出前三次着地后反弹的高度,找出规律,即可解答.
【详解】解:(1)小球第2次着地时,经过的总路程为:,
故答案为:6;
(2)第1次着地后反弹的高度为:,
第2次着地后反弹的高度为:,
第3次着地后反弹的高度为:,
…
第n次着地后反弹的高度为:,
故答案为:.
【点睛】本题考查了实际问题中的规律探究问题,解答本题的关键是明确题意,找出题目中数的变化规律,注意每次着地后又跳回到原高度的一半再落下.
19.7
【分析】根据有理数的绝对值以及乘方的意义化简各数后即可得到答案.
【详解】解:|﹣3|+(﹣2)2
=3+4
=7
【点睛】此题主要考查了有理数的运算,正确化简各数是解答此题的关键.
20.
【分析】本题首先算括号里面的,然后小数化分数,最后依次计算.
【详解】原式=
故答案为
【点睛】本题注意的是运算顺序和除法法则,有括号先算括号里面的,除以一个数相当于乘以这个数的倒数.
21.表示见详解,
【分析】先化简,再把各数在数轴上表示出来,最后根据数轴用“<”连接接可.
【详解】解:,
在数轴上表示各数如图:
所以.
【点睛】本题考查了用数轴上的点表示有理数,有理数的化简,有理数的大小比较等知识,把有关数据进行化简是解题关键.
22.(1)人
(2)不超过
【分析】(1)设每轮感染中平均一个人传染人,根据题意列方程解方程即可;
(2)根据(1)可知每轮感染中平均一个人传染人,进而得到三轮后患病总人数为即可解答.
【详解】(1)解:设每轮感染中平均一个人传染人.
根据题意得,
解得,或,
∵,
∴,
答:每轮感染中平均一个人传染人;
(2)解:根据题意可得:
第三轮的患病人数为,
∵,
∴经过三轮传染后累计患甲流的人数不会超过人,
答:经过三轮传染后累计患甲流的人数不超过人;
【点睛】本题考查了一元二次方程与实际问题,读懂题意明确数量关系是解题的关键.
23.(1)211﹣1
(2)1+3+32+33+34+…+3n=.
【分析】(1)设S=1+2+22+23+24+…+210,两边乘以2后得到关系式,与已知等式相减,变形即可求出所求式子的值.
(2)同理即可得到所求式子的值.
【详解】解:(1)设S=1+2+22+23+24+…+210,
将等式两边同时乘以2得2S=2+22+23+24+…+210+211,
将下式减去上式得:2S﹣S=211﹣1,即S=211﹣1,
则1+2+22+23+24+…+210=211﹣1.
(2)设S=1+3+32+33+34+…+3n,
两边乘以3得:3S=3+32+33+34+…+3n+3n+1,
下式减去上式得:3S﹣S=3n+1﹣1,即S=,
则1+3+32+33+34+…+3n=.
24.(1)3;(2);(3)
【分析】设塔的顶层共有盏灯,根据题意列出方程,进行解答即可.
参照题目中的解题方法进行计算即可.
由题意求得数列的每一项,及前n项和Sn=2n+1-2-n,及项数,由题意可知:2n+1为2的整数幂.只需将-2-n消去即可,分别分别即可求得N的值
【详解】设塔的顶层共有盏灯,由题意得
.
解得,
顶层共有盏灯.
设,
,
即:
.
即
由题意可知:20第一项,20,21第二项,20,21,22第三项,…20,21,22…,2n−1第n项,
根据等比数列前n项和公式,求得每项和分别为:
每项含有的项数为:1,2,3,…,n,
总共的项数为
所有项数的和为
由题意可知:为2的整数幂,只需将−2−n消去即可,
则①1+2+(−2−n)=0,解得:n=1,总共有,不满足N>10,
②1+2+4+(−2−n)=0,解得:n=5,总共有 满足,
③1+2+4+8+(−2−n)=0,解得:n=13,总共有 满足,
④1+2+4+8+16+(−2−n)=0,解得:n=29,总共有 不满足,
∴
【点睛】考查归纳推理,读懂题目中等比数列的求和方法是解题的关键.









