高中数学人教A版 (2019)必修 第一册3.1 函数的概念及其表示课文ppt课件

这是一份高中数学人教A版 (2019)必修 第一册3.1 函数的概念及其表示课文ppt课件，共40页。PPT课件主要包含了必备知识•探新知，数学表达式，关键能力•攻重难，fx＝x2＋1，课堂检测•固双基，x－1等内容，欢迎下载使用。

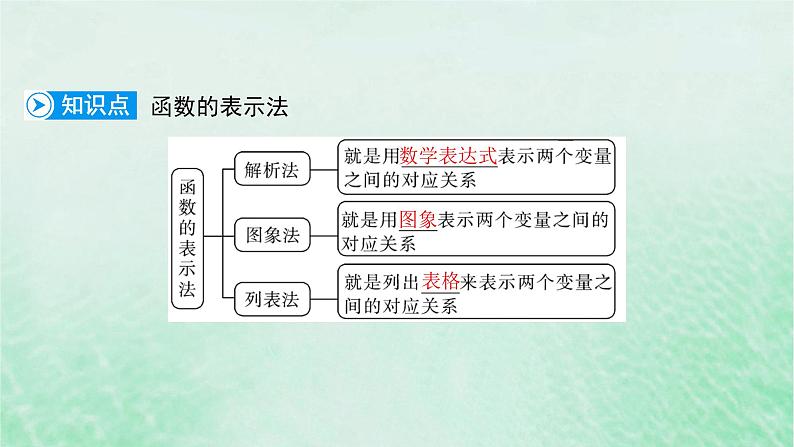
3.1　函数的概念及其表示3.1.2　函数的表示法第1课时　函数的表示法
1．掌握函数的三种表示方法：解析法、图象法、列表法．2．会根据不同的需要选择恰当的方法表示函数．1．通过函数表示的图象法培养直观想象素养．2．通过函数解析式的求法培养数学运算素养.
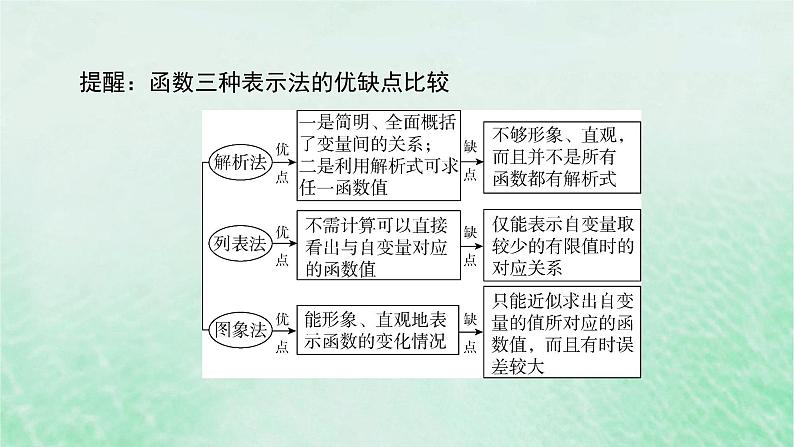
提醒：函数三种表示法的优缺点比较
想一想：任何一个函数都可以用解析法、列表法、图象法三种形式表示吗？
练一练：1．已知函数y＝f(x)的图象如图，则f(x)的定义域是( )A．(－∞，1)∪(1，＋∞)B．RC．(－∞，0)∪(0，＋∞)D．(－1,0)[解析]　由图象，知x≠0，即x∈(－∞，0)∪(0，＋∞)．
2．二次函数的图象的顶点为(0，－1)，对称轴为y轴，则二次函数的解析式可以为( )
[解析]　把点(0，－1)代入四个选项可知，只有B正确．故选B.
3．已知函数f(x)，g(x)分别由下表给出：则f[g(1)]的值为____；当g[f(x)]＝2时，x＝____.
[解析]　由g(x)对应表，知g(1)＝3，所以f[g(1)]＝f(3)．由f(x)对应表，得f(3)＝1，所以f[g(1)]＝f(3)＝1.由g(x)对应表，得当x＝2时，g(2)＝2，又g[f(x)]＝2，所以f(x)＝2.又由f(x)对应表，得x＝1时，f(1)＝2.所以x＝1.
某问答游戏的规则是：共答5道选择题，基础分为50分，每答错一道题扣10分，答对不扣分．试分别用列表法、图象法、解析法表示一个参与者的得分y与答错题目道数x(x∈{0,1,2,3,4,5})之间的函数关系y＝f(x)．[解析]　(1)用列表法可将函数y＝f(x)表示为
(2)用图象法可将函数y＝f(x)表示为(3)用解析法可将函数y＝f(x)表示为y＝50－10x，x∈{0,1,2,3,4,5}．
[归纳提升]　1.函数的三种表示法的选择解析法、图象法和列表法分别从三个不同的角度刻画了自变量与函数值的对应关系．采用解析法的前提是变量间的对应关系明确，采用图象法的前提是函数的变化规律清晰，采用列表法的前提是定义域内自变量的个数较少．2．用三种表示法表示函数时的注意点(1)解析法必须注明函数的定义域；(2)列表法必须罗列出所有的自变量的值与函数值的对应关系；(3)图象法必须清楚函数图象是“点”还是“线”．
已知函数f(x)＝－x－1，x∈{1,2,3,4}，试分别用列表法和图象法表示函数y＝f(x)．[解析]　用列表法表示函数y＝f(x)，如表所示.用图象法表示函数y＝f(x)，如图所示．
[分析]　(1)画函数的图象时首先要注意的是什么？(2)所给三个函数的大致图象分别是什么形式的？
(3)列表画图象，图象是抛物线y＝x2＋2x在－2≤x≤2之间的部分．
由图可得函数的值域是[－1,8]．
[归纳提升]　描点法作函数图象的三个关注点(1)画函数图象时首先关注函数的定义域，即在定义域内作图；(2)图象是实线或实点，定义域外的部分有时可用虚线来衬托整个图象；(3)要标出某些关键点，例如图象的顶点、端点、与坐标轴的交点等．要分清这些关键点是实心点还是空心圈．提醒：函数图象既可以是连续的曲线，也可以是直线、折线、离散的点等．
角度1　待定系数法求解析式 (1)已知一次函数f(x)满足f[f(x)]＝4x＋6，则f(x)的解析式为_______________________________.(2)已知二次函数f(x)满足f(0)＝1，f(1)＝2，f(2)＝5，则该二次函数的解析式为________________.[分析]　已知函数类型分别为一次函数和二次函数，设出函数解析式求出参数即可．
f(x)＝2x＋2或f(x)＝－2x－6
(2)已知函数f(x＋1)＝x2－2x，则f(x)的解析式为_________________.
f(x)＝x2－4x＋3
[分析]　已知f[g(x)]求f(x)有两种思路：一是将g(x)视为一个整体，应用数学的整体化思想，换元求解；二是将函数解析式的右端凑成含g(x)的形式．
(2)解法一(换元法)　令x＋1＝t，则x＝t－1，t∈R，所以f(t)＝(t－1)2－2(t－1)＝t2－4t＋3，即f(x)＝x2－4x＋3.解法二(配凑法)　因为x2－2x＝(x2＋2x＋1)－(4x＋4)＋3＝(x＋1)2－4(x＋1)＋3，所以f(x＋1)＝(x＋1)2－4(x＋1)＋3，即f(x)＝x2－4x＋3.
[归纳提升]　函数解析式的求法(1)待定系数法：若已知函数的类型(如一次函数、二次函数)，可用待定系数法．(2)换元法：已知复合函数f[g(x)]的解析式，可用换元法，此时要注意新元的取值范围．
[解析]　(1)设f(x)＝ax2＋bx＋c(a≠0)，则f(x＋1)＋f(x－1)＝a(x＋1)2＋b(x＋1)＋c＋a(x－1)2＋b(x－1)＋c＝2ax2＋2bx＋2a＋2c＝2x2－4x，
1．由下表给出函数y＝f(x)，则f[f(1)]等于( )A．1　　　　　　　　B．2C．4 D．5[解析]　由题意可知，f(1)＝4，f(4)＝2，∴f[f(1)]＝f(4)＝2.故选B.
2．如图，函数f(x)的图象是折线段，其中点A，B，C的坐标分别是(0,4)，(2,0)，(6,4)，则f[f(2)]＝( )A．0 B．2C．4 D．6[解析]　由图象可得f[f(2)]＝f(0)＝4.
3．已知函数f(x＋1)＝3x＋2，则f(x)＝__________.[解析]　解法一(换元法)：令x＋1＝t，∴x＝t－1，∴f(t)＝3(t－1)＋2＝3t－1，∴f(x)＝3x－1.解法二(配凑法)：f(x＋1)＝3x＋2＝3(x＋1)－1，∴f(x)＝3x－1.