





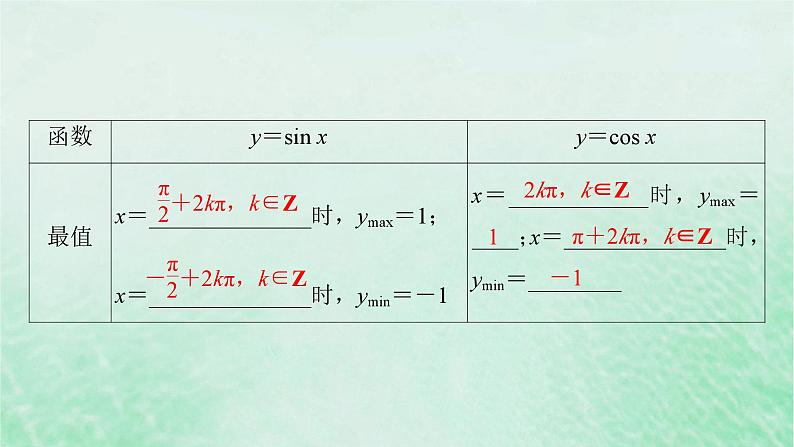
所属成套资源:新教材适用2023_2024学年高中数学新人教A版必修第一册全册课件(61份)
- 新教材适用2023_2024学年高中数学第5章三角函数5.3诱导公式第2课时诱导公式二课件新人教A版必修第一册 课件 0 次下载
- 新教材适用2023_2024学年高中数学第5章三角函数5.4三角函数的图象与性质5.4.2正弦函数余弦函数的性质第1课时周期性与奇偶性课件新人教A版必修第一册 课件 0 次下载
- 新教材适用2023_2024学年高中数学第5章三角函数5.4三角函数的图象与性质5.4.3正切函数的性质与图象课件新人教A版必修第一册 课件 0 次下载
- 新教材适用2023_2024学年高中数学第5章三角函数5.5三角恒等变换5.5.1两角和与差的正弦余弦和正切公式第1课时两角差的余弦公式课件新人教A版必修第一册 课件 0 次下载
- 新教材适用2023_2024学年高中数学第5章三角函数5.5三角恒等变换5.5.1两角和与差的正弦余弦和正切公式第2课时两角和与差的正弦余弦公式课件新人教A版必修第一册 课件 0 次下载
人教A版 (2019)必修 第一册5.4 三角函数的图象与性质背景图课件ppt
展开
这是一份人教A版 (2019)必修 第一册5.4 三角函数的图象与性质背景图课件ppt,共40页。PPT课件主要包含了必备知识•探新知,-11,k∈Z,2kππ+,kπk∈Z,π+2kπk∈Z,-π0,关键能力•攻重难,cos150°,课堂检测•固双基等内容,欢迎下载使用。
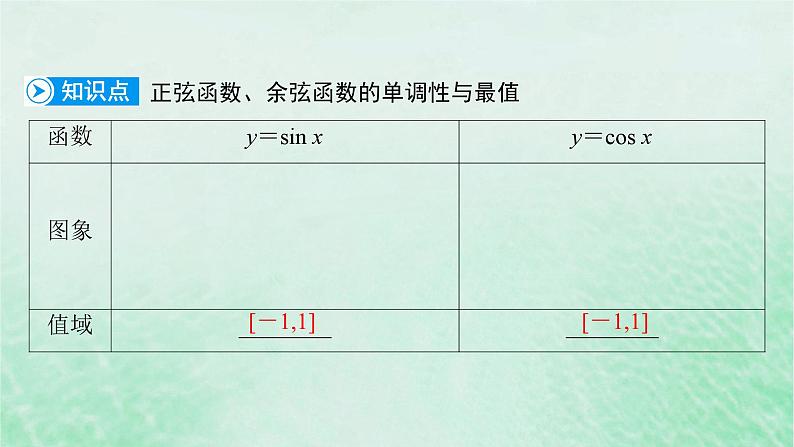
5.4 三角函数的图象与性质5.4.2 正弦函数、余弦函数的性质第2课时 单调性与最值
1.掌握y=sin x,y=cs x的最大值与最小值,并会求简单三角函数的值域和最值.2.掌握y=sin x,y=cs x的单调性,并能利用单调性比较大小.3.会求函数y=Asin(ωx+φ)及y=Acs(ωx+φ)的单调区间.1.通过单调性与最值的计算,提升数学运算素养.2.结合函数图象,培养直观想象素养.
[-π+2kπ,2kπ],k∈Z
提醒:(1)体现了正、余弦函数的有界性,即|sin x|≤1,|cs x|≤1;(2)正弦函数、余弦函数的增区间、减区间交替变化,都有无数个;(3)函数y=sin x,y=cs x在图象的波峰(波谷)取得最大(小)值.
想一想:正弦函数y=sin x是奇函数,正弦曲线关于原点对称,即原点是正弦曲线的对称中心.(1)除原点外,正弦曲线还有其他对称中心吗?如果有,那么对称中心的坐标是多少?(2)正弦函数是轴对称图形吗?如果是,对称轴的方程是什么?(3)余弦函数y=cs x呢?有以上的性质吗?
练一练:1.判断下列说法是否正确,正确的打“√”,错误的打“×”.(1)正弦函数y=sin x在R上是单调函数.( )提示:正弦函数y=sin x在R上不是单调函数.(2)余弦函数y=cs x的一个减区间是[0,π].( )(3)∃x∈[0,2π]满足sin x=2.( )提示:因为|sin x|≤1,故不存在使sin x=2的x值.
2.函数y=2-sin x取得最大值时x的值为__________________.
3.函数y=2cs x在区间[-π,π]上的单调递增区间是___________.[解析] 函数y=2cs x在区间[-π,π]上的单调递增区间与y=cs x的相同,为[-π,0].
[分析] (1)可采用整体换元法并结合正弦函数、余弦函数的单调区间求解;(2)可先将自变量x的系数转化为正数再求单调区间.
[归纳提升] 1.求形如y=Asin(ωx+φ)+b或形如y=Acs(ωx+φ)+b(其中A≠0,ω>0,b为常数)的函数的单调区间,可以借助于正弦函数、余弦函数的单调区间,通过解不等式求得.2.具体求解时注意两点:(1)要把ωx+φ看作一个整体,若ω0,ω>0时,将“ωx+φ”代入正弦(或余弦)函数的单调区间,可以解得与之单调性一致的单调区间;当A0时同样方法可以求得与正弦(余弦)函数单调性相反的单调区间.提醒:复合函数的单调性遵循“同增异减”的规律.
利用三角函数的单调性,比较下列各组数的大小.(2)cs 1,sin 1;(3)sin 164°与cs 110°.
(3)sin 164°=sin(180°-16°)=sin 16°,cs 110°=cs(90°+20°)=-sin 20°.因为sin 16°>0,-sin 20°
相关课件
这是一份高中数学人教A版 (2019)必修 第一册5.4 三角函数的图象与性质课前预习课件ppt,共21页。PPT课件主要包含了导入新课,精彩课堂,应用举例,课堂练习,π+2kπk∈Z,课堂总结等内容,欢迎下载使用。
这是一份高中人教A版 (2019)5.4 三角函数的图象与性质课文内容ppt课件,共42页。PPT课件主要包含了-11,kπk∈Z,答案C,答案1D,答案1B,答案1等内容,欢迎下载使用。
这是一份人教A版 (2019)必修 第一册5.4 三角函数的图象与性质示范课课件ppt,共33页。PPT课件主要包含了素养·目标定位,课前·基础认知,课堂·重难突破,随堂训练,典例剖析,学以致用,答案B,答案D等内容,欢迎下载使用。









