【期中真题】（苏科版）2023-2024学年七年级数学上学期期中真题分类专题汇编 专题07一元一次方程解决问题（7种题型）.zip

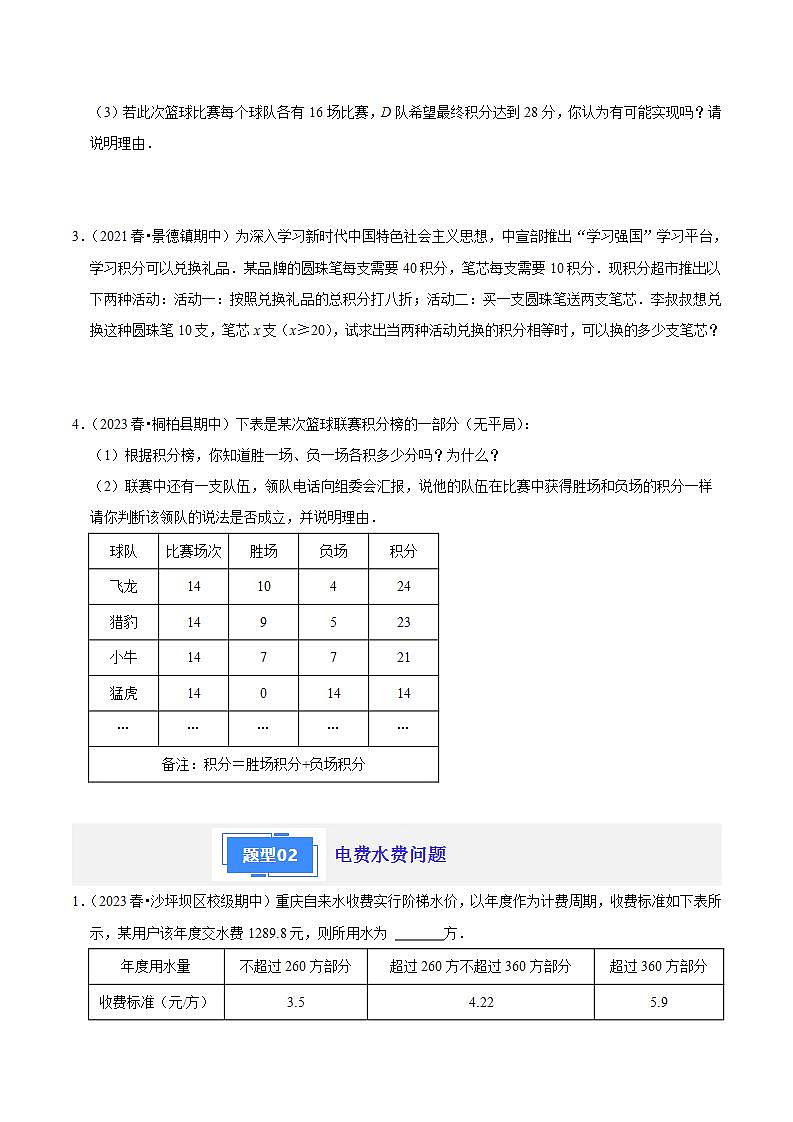
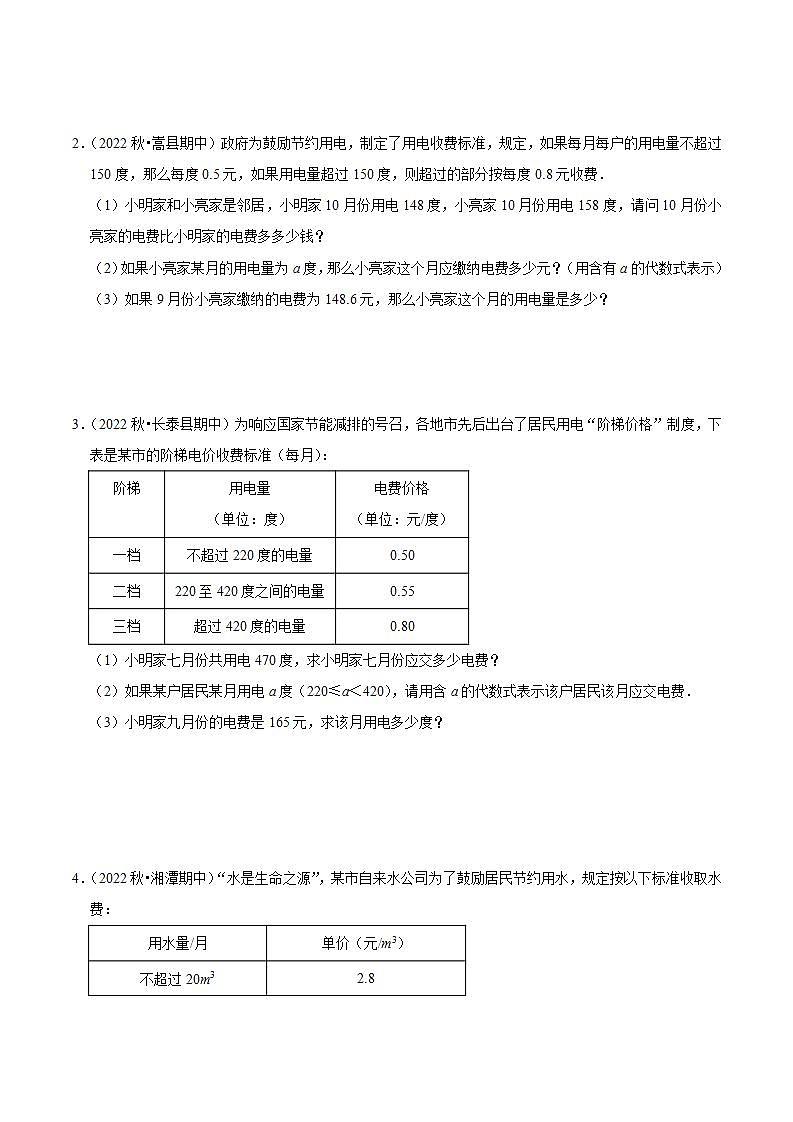
专题07 一元一次方程解决问题 比赛积分问题1．（2022秋•香坊区校级期中）在2012年伦敦奥运会足球赛的前11场比赛中，某队仅负1场，共积22分，按比赛规则，胜一场得3分，平一场得1分，负一场得0分，则该队共胜了（　　）场．A．4 B．5 C．6 D．72．（2021秋•建瓯市校级期中）表为某篮球比赛过程中部分球队的积分榜（篮球比赛过程中没有平局）．（1）观察积分榜，请写出球队胜一场积 　　分，负一场积 　　分．（2）根据积分规则，请求出E队已经进行的10场比赛中，胜、负各是多少场？（3）若此次篮球比赛每个球队各有16场比赛，D队希望最终积分达到28分，你认为有可能实现吗？请说明理由．3．（2021春•景德镇期中）为深入学习新时代中国特色社会主义思想，中宣部推出“学习强国”学习平台，学习积分可以兑换礼品．某品牌的圆珠笔每支需要40积分，笔芯每支需要10积分．现积分超市推出以下两种活动：活动一：按照兑换礼品的总积分打八折；活动二：买一支圆珠笔送两支笔芯．李叔叔想兑换这种圆珠笔10支，笔芯x支（x≥20），试求出当两种活动兑换的积分相等时，可以换的多少支笔芯？4．（2023春•桐柏县期中）下表是某次篮球联赛积分榜的一部分（无平局）：（1）根据积分榜，你知道胜一场、负一场各积多少分吗？为什么？（2）联赛中还有一支队伍，领队电话向组委会汇报，说他的队伍在比赛中获得胜场和负场的积分一样请你判断该领队的说法是否成立，并说明理由． 电费水费问题1．（2023春•沙坪坝区校级期中）重庆自来水收费实行阶梯水价，以年度作为计费周期，收费标准如下表所示，某用户该年度交水费1289.8元，则所用水为 　 　方．2．（2022秋•嵩县期中）政府为鼓励节约用电，制定了用电收费标准，规定，如果每月每户的用电量不超过150度，那么每度0.5元，如果用电量超过150度，则超过的部分按每度0.8元收费．（1）小明家和小亮家是邻居，小明家10月份用电148度，小亮家10月份用电158度，请问10月份小亮家的电费比小明家的电费多多少钱？（2）如果小亮家某月的用电量为a度，那么小亮家这个月应缴纳电费多少元？（用含有a的代数式表示）（3）如果9月份小亮家缴纳的电费为148.6元，那么小亮家这个月的用电量是多少？3．（2022秋•长泰县期中）为响应国家节能减排的号召，各地市先后出台了居民用电“阶梯价格”制度，下表是某市的阶梯电价收费标准（每月）：（1）小明家七月份共用电470度，求小明家七月份应交多少电费？（2）如果某户居民某月用电a度（220≤a＜420），请用含a的代数式表示该户居民该月应交电费．（3）小明家九月份的电费是165元，求该月用电多少度？4．（2022秋•湘潭期中）“水是生命之源”，某市自来水公司为了鼓励居民节约用水，规定按以下标准收取水费：（1）根据上表，用水量每月不超过20m3，实际每立方米收水费　　元；如果1月份某用户用水量为19m3，那么该用户1月份应该缴纳水费　　元；（2）某用户2月份共缴纳水费80元，那么该用户2月份用水多少m3？（3）若该用户水表3月份出了故障，只有70%的用水量记入水表中，这样该用户在3月份只缴纳了58.8元水费，问该用户3月份实际应该缴纳水费多少元？ 方案选择问题1．（2022春•叙州区校级期中）某校七年级准备观看电影《长津湖》，由各班班长负责买票，每班人数都多于40人，票价每张30元，一班班长问售票员买团体票是否可以优惠，售票员说：40人以上的团体票有两种优惠方案可选择：方案一：全体人员可打8折；方案二：若打9折，有5人可以免票．（1）若二班有42名学生，则他该选择哪个方案？（2）一班班长思考一会儿说，我们班无论选择哪种方案要付的钱是一样的，你知道一班有多少人吗？2．（2023春•恩阳区 期中）天虹超市销售东北大米，每包10kg，定价为100元．元旦期间进行促销活动，为满足大宗采购需求，超市制定了两种销售方案以供选择：方案一：六折优惠并且免费送货上门；方案二：买一送一，但需另付200元运费．（1）假设某食堂需要财买8包东北大米，且需送货上门．采用方案一购买，需要 　 　元；采用方案二购买，需要 　 　元．（2）假设某食堂需要购买x包东北大米（x是偶数），且需送货上门．①采用方案一购买x包东北大米需要 　 　元；采用方案二购买x包东北大米需要 　 　元．②某次进货时，食堂的采购员小王发现两种采购方案相差100元．请你算一算小王这次采购多少包东北大米？3．（2022秋•贵州期中）2021年“双十一”期间，很多国货品牌受到人们的青睐，销量大幅增长．某平台的体育用品旗舰店实行优惠销售，规定如下：对原价160元/件的某款运动速干衣和20元/双的某款运动棉袜开展促销活动，活动期间向客户提供两种优惠方案．方案A：买一件运动速干衣送一双运动棉袜；方案B：运动速干衣和运动棉袜均按9折付款．某户外俱乐部准备购买运动速干衣30件，运动棉袜x双（x≥30）．（1）若该户外俱乐部按方案A购买，需付款 　 　元（用含x的式子表示）；若该户外俱乐部按方案B购买，需付款 　 　元（用含x的式子表示）；（2）若x＝40，通过计算说明此时按哪种方案购买较为合算；（3）当购买运动棉袜多少双时两种方案付款相同． 工程问题1．（2022秋•贵州期中）一条地下管线由甲工程队单独铺设需要12天，则乙工程队单独铺设需要24天，如果由这两个工程队从两端同时施工，铺好这条管线需要的天数是（　　）A．8天 B．7天 C．6天 D．5天2．（2023春•农安县期中）一项工程，甲队单独完成需要40天，乙队单独完成需要50天，现甲队单独做4天后两队合作．（1）求甲、乙两队合作多少天才能完成该工程．（2）在（1）的条件下，甲队每天的施工费为3000元，乙队每天的施工费为3500元，求完成此项工程需付给甲乙两队共多少元．3．（2022秋•渝中区校级期中）一项工程，甲队单独完成需30天，乙队单独完成需45天，现甲队先单独做20天，之后两队合作．（1）甲、乙合作多少天才能把该工程完成？（2）甲队施工一天需付工程款3.5万元，乙队施工一天需付工程款2万元．若该工程计划在40天内完成，在不超过计划天数的前提下，是由甲队或乙队单独完成该工程省钱？还是由甲、乙两队全程合作完成该工程省钱？4．（2022秋•奉贤区期中）区域需要将一段长为120米的绿化带进行整修，整修任务由甲、乙两个工程队先后接力共同完成．已知甲工程队每天可以整修8米，乙工程队每天可以整修6米，两个工程队共用了18天，问甲、乙两个工程队整修绿化带分别参加了几天？配套问题1．（2022春•五华区校级期中）某车间有66名工人，每名工人一天能生产甲种零件24个或生产乙种零件15个，而甲种零件3个，乙种零件5个配成一套机件，请合理分配所有工人，使得每天生产的零件刚好配套，则每天可生产 　 　套．2．（2023春•丰泽区校级期中）用白铁皮做罐头盒，每张铁皮可制盒身25个，或制盒底40个，一个盒身与两个盒底配成一套．现在有36张白铁皮，用多少张制盒身，多少张制盒底，可使盒身与盒底正好配套？3．（2023春•鲤城区校级期中）某医疗器械企业计划购进20台机器生产口罩，已知生产口罩面的机器每台每天的产量为12000个，生产耳挂绳的机器每台每天的产量为96000个，口罩是一个口罩面和两个耳挂绳构成，为使每天生产的口罩面和耳挂绳刚好配套，该企业应分别购进生产口罩面和生产耳挂绳的机器各多少台？4．（2022春•祁阳县校级期中）工业园区某机械厂的一个车间主要负责生产螺丝和螺母，该车间有工人44人，其中女生人数比男生人数的2倍少10人，每个工人平均每天可以生产螺丝50个或者螺母120个．（1）该车间有男生、女生各多少人？（2）已知一个螺丝与两个螺母配套，为了使每天生产的螺丝螺母恰好配套，应该分配多少工人负责生产螺丝，多少工人负责生产螺母？销售问题1．（2021秋•诸暨市校级期中）一件商品，先提价10%，再降价10%，那么售价比原价（　　）A．贵了 B．便宜了 C．都一样 D．价格不知道，不能确定2．（洛龙区校级期中）某商品按进价增加20%出售，因积压需降价处理，如果仍想获得8%的利润，则出售价需打　 　折．3．（2022春•闵行区校级期中）一种节能型冰箱，商家计划按进价加价20%作为售价，为了促销，商家现在按原售价的九折出售了40台，降价后的新售价是每台2430元．（1）按照新售价出售，商家每台冰箱还可赚多少元？（2）售完这批冰箱后，商家将购进40台冰箱的进货款存入银行，存期一年，不扣利息税到期可得人民币92025元，求这项储蓄的年利率是多少？4．（2023春•闵行区期中）一种节能型冰箱，商店按原售价的九折出售，降价后的新售价是每台2430元．因为商店按进价加价20%作为原售价，所以降价后商店还能赚线．请问：这种节能型冰箱的进价是多少元？按降价后的新售价出售，商店每台还可赚多少元？题型7 行程问题1．（2021秋•南岗区校级期中）A，B两地相距450千米，甲、乙两车分别从A，B两地同时出发，相向而行，已知甲车速度为120千米/小时，乙车速度为80千米/小时，则经过　　小时，两车相距50千米．2．（2023春•平桂区 期中）张明家离学校5千米，某天17：30他乘坐公车返校，十分钟后到站下车步行，计划18：00前赶到学校，若公车的速度为每小时24千米，则他下车步行每小时至少走 　　千米．3．（2022秋•郑州期中）如图，在数轴上，O为原点，点A对应的数为2，点B对应的数为﹣12．在数轴上有两动点C和D，它们同时向右运动，点C从点A出发，速度为每秒4个单位长度，点D从点B出发，速度为每秒6个单位长度，设运动时间为t秒，当点O，C，D中，其中一点正好位于另外两点所确定线段的中点时，t的值为 　　．4．（2023春•绿园区校级期中）A，B两地之间有一条长为600千米的公路，甲乙两车都从A地匀速开往B地，乙车出发1小时后甲车再出发，乙车行驶4小时后被甲车追上，乙车行驶8.5小时后甲车已到达目的地B地，两车分别到达目的地后停在B地．（1）甲的速度为 　　千米/时，乙的速度为 　　千米/时．（2）当甲车与乙车相距的路程为80千米时，求此时乙车行驶的时间．一．选择题1．已知有理数a，b，c在数轴上对应的点分别为A，B，C，且a＝﹣2，b＝1，c＝5．若点A，B，C分别以每秒4个单位长度，1个单位长度，1个单位长度的速度在数轴上同时向右运动，设运动时间为t秒，当点A在点B左侧，且AC长为6时，t的值为（　　）A． B．1 C． D．22．如图，甲、乙两人沿着边长为90m的正方形，按A→B→C→D→A的方向行走，甲从点A出发，以50m/min的速度行走；同时，乙从点B出发，以65m/min的速度行走．当乙第一次追上甲时，在正方形的（　　）A．BC边上 B．AD边上 C．点C处 D．点D处3．如图，数轴上点A和点B表示的数分别是﹣6和4，动点M从A点以每秒3cm的速度匀速向右移动，动点N同时从B点以每秒1cm的速度匀速向右移动．设移动时间为t秒，当动点N到原点的距离是动点M到原点的距离的2倍时，t的值为（　　）A． B． C．或 D．或4．一列火车匀速行驶，经过一条长800米的隧道，从车头开始进入隧道到车尾离开隧道共需要50秒的时间，在隧道中央的顶部有一盏灯，垂直向下发光照到火车上的时间是18秒，则这列火车行驶的速度是（　　）米/秒．A．25 B．30 C．35 D．405．一艘船从甲码头顺流而行至乙码头需7h，从乙码头逆流而行返回甲码头需8.5h．已知水流速度为3km/h，则船在静水中的平均速度为（　　）A．28.5km/h B．31km/h C．35km/h D．46.5km/h6．如图，已知A，B两点在数轴上，点A表示的数为﹣10，OB＝2OA，点M以每秒1个单位长度的速度从点A向右运动，点N以每秒3个单位长度的速度从点B向左运动（点M、点N同时出发），经过几秒，点M、点N分别到原点O的距离相等（　　）A．5秒 B．5秒或者4秒 C．5秒或者秒 D．秒二．填空题7．甲、乙二人分别从A、B两地出发相向而行．如果二人同时出发，则12小时相遇；如果甲走全程需要20小时，则甲、乙二人的速度比是 　 ．8．《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有善行者行一百步，不善行者行六十步．今不善行者先行八十步，善行者追之，问几何步及之？“其意思为：速度快的人走100步，速度慢的人只走60步，现速度慢的人先走80步，速度快的人去追赶，则速度快的人要走 　 　步才能追到速度慢的人．9．如图，矩形ABCD中，AB＝8cm，BC＝12cm，动点P从点A出发沿A﹣B﹣C﹣D﹣A运动，速度是2cm/秒；点Q从点C出发沿C﹣B﹣A﹣D﹣C运动，速度是4cm/秒，设它们的运动时间为t秒．（1）当t＝1时，连接PQ，PQ＝　　cm；（2）若P、Q两点第一次相遇时，t＝　　秒；第2次相遇时，t＝　　秒．10．A、B两个港口相距180公里．若甲船顺水自A驶向B，乙船同时自B逆水驶向A，两船在C处相遇；若乙船顺水自A驶向B，甲船同时自B逆水驶向A，则两船在D处相遇．已知CD相距30公里，甲船速度为35公里/小时，则乙船的速度为 　　公里/小时．11．某校运会在400米环形跑道上进行10000米比赛，甲、乙两运动员同时起跑后，乙速超过甲速，在第15分钟时，甲加快速度，在第18分钟时甲追上乙并且开始超过乙，在第23分钟时，甲再次追上乙．那么，开始时乙每分钟比甲多跑 　　米，甲加速后，每分钟比原来多跑 　　米．12．某医院10月8日上午派遣了甲、乙两支核酸检测队伍，分别前往两个不同的学校为全校师生做核酸检测，已知每个医务人员的检测速度相同，甲队伍医务人员的人数是乙队伍的4倍，两队伍检测时长相同，下午两支队伍又分别前往两个社区做核酸检测，甲队伍检测人员不变，每个医务人员的检测速度增加了，乙队伍检测人员和每个医务人员的检测速度都不变，两个队伍需检测的人数都增加，且甲队伍增加的人数是乙队伍增加的人数的4倍，甲、乙两支队伍下午的检测时间之比为 　　．三．解答题13．甲、乙两地相距720千米．一辆汽车从甲地匀速开往乙地，已经行驶了4小时，剩下的路程比已经行驶的多40千米．这辆汽车的速度是多少千米/时？14．如图，数轴上A、B两点对应的有理数分别为10和15，点P从点A出发，以每秒1个单位长度的速度沿数轴正方向运动，点Q同时从原点O出发，以每秒2个单位长度的速度沿数轴正方向运动，设运动时间为t秒．（1）当0＜t＜5时，用含t的式子表示BP和AQ；（2）当t＝2时，求PQ的值；（3）当PQ时，求t的值．15．甲、乙两地之间的高速公路全长760千米，一辆客车和一辆货车同时从甲、乙两地出发，相向而行，经过4小时相遇．如果客车的速度是110千米/时，货车的速度是多少千米/时？（列方程解）16．一个自行车队进行训练，训练时所有队员都以30km/h的速度前进．突然，1号队员以50km/h的速度独自行进，行进20km后掉转车头，仍以50km/h的速度往回骑，直到与其他队员会合．1号队员从离队开始到与队员重新会合，经过了多长时间？17．已知数轴上两点A，B对应的数分别为﹣6，4，O为原点．（1）若点P为线段AB上一点，且点P到点A的距离是点P到点B的距离的4倍，求点P对应的数；（2）当点B以每秒2个单位长度的速度向右运动时，点A以每秒3个单位长度的速度向右运动，问他们同时出发，几秒后A，B，O其中一点是连接另外两点的线段的中点？18．阅读理解：若A、B、C为数轴上三点，点C到A的距离是点C到B的距离2倍，我们就称点C是[A，B]的好点．例如，如图1，点A表示的数为﹣1，点B表示的数为2．表示数1的点C到点A的距离是2，到点B的距离是1，那么点C是[A，B]的好点．知识运用：如图2，M、N为数轴上两点，点M所表示的数为﹣2，点N所表示的数为4．（1）线段MN上存在一点是[M，N]的好点，则此点表示的数是 　　；（2）如图3，A、B为数轴上两点，点A所表示的数为﹣20，点B所表示的数为40．现有一只电子蚂蚁P从点B出发，以2个单位每秒的速度向左运动，到达点A停止．当运动时间t为何值时，点P、A、B中恰有一个点为其余两点的好点？（3）在（2）条件下，若点P到达A点后继续向左运动，当P为[B，A]的好点时，请直接写出线段PB的长及此时点P表示的数．球队比赛场次胜场负场积分A1210222B128420C127519D115616E10……15球队比赛场次胜场负场积分飞龙1410424猎豹149523小牛147721猛虎1401414……………备注：积分＝胜场积分+负场积分年度用水量不超过260方部分超过260方不超过360方部分超过360方部分收费标准（元/方）3.54.225.9阶梯用电量（单位：度）电费价格（单位：元/度）一档不超过220度的电量0.50二档220至420度之间的电量0.55三档超过420度的电量0.80用水量/月单价（元/m3）不超过20m32.8超过20m3的部分3.8另：每立方米用水加收0.2元的城市污水处理费