【期中真题】（北师大版）2023-2024学年七年级数学上册 期中真题分类专题汇编 专题02 有理数的相关概念（九大题型）.zip

这是一份【期中真题】（北师大版）2023-2024学年七年级数学上册 期中真题分类专题汇编 专题02 有理数的相关概念（九大题型）.zip，文件包含期中真题北师大版2023-2024学年七年级数学上册期中真题分类专题汇编专题02有理数的相关概念原卷版docx、期中真题北师大版2023-2024学年七年级数学上册期中真题分类专题汇编专题02有理数的相关概念解析版docx等2份试卷配套教学资源，其中试卷共36页， 欢迎下载使用。

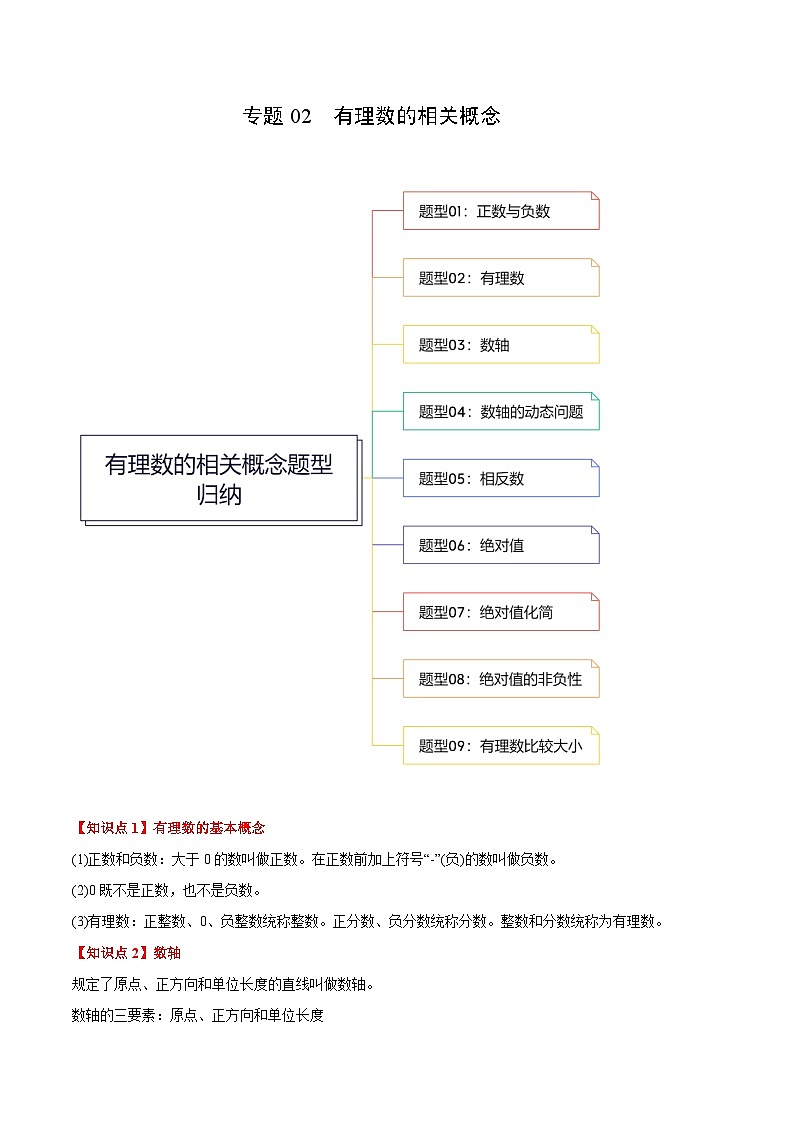
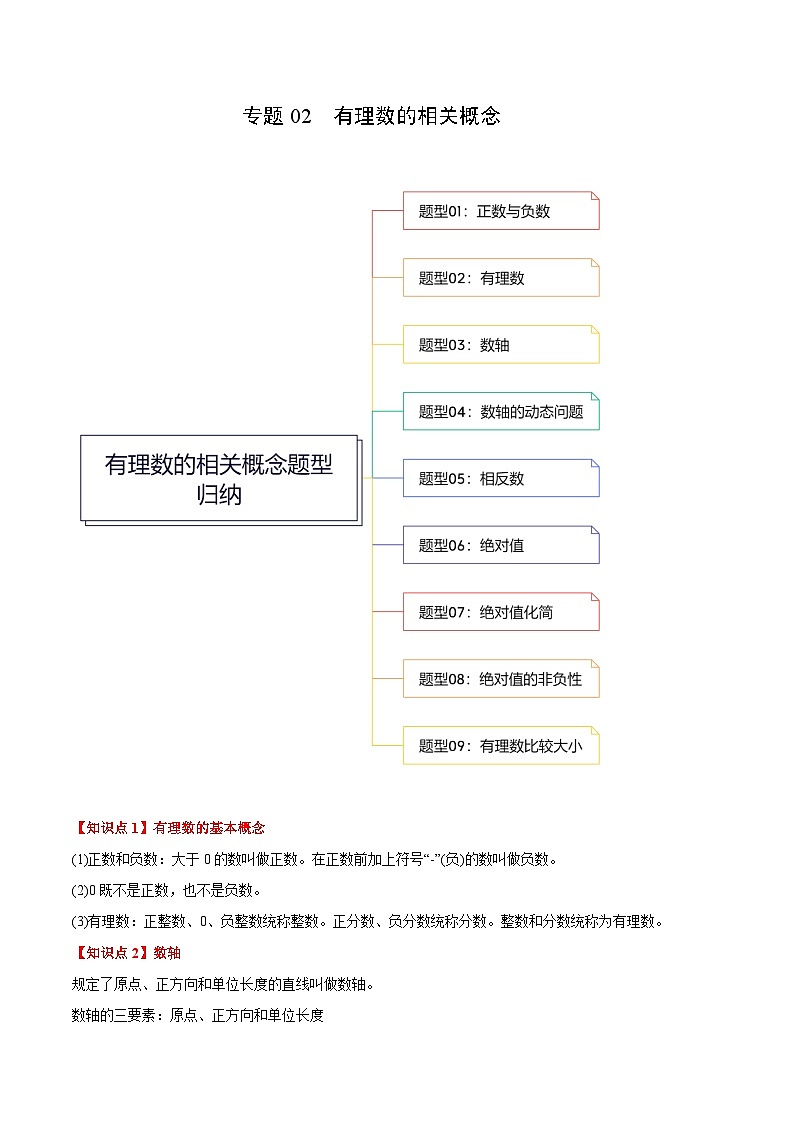
专题02 有理数的相关概念



【知识点1】有理数的基本概念
(1)正数和负数：大于0的数叫做正数。在正数前加上符号“-”(负)的数叫做负数。
(2)0既不是正数，也不是负数。
(3)有理数：正整数、0、负整数统称整数。正分数、负分数统称分数。整数和分数统称为有理数。
【知识点2】数轴
规定了原点、正方向和单位长度的直线叫做数轴。
数轴的三要素：原点、正方向和单位长度
【知识点3】相反数
代数定义：只有符号不同的两个数叫做互为相反数。
几何定义：在数轴上原点的两旁，离开原点距离相等的两个点所表示的数，叫做互为相反数。
一般地，a和-a互为相反数。0的相反数是0。
a =-a所表示的意义是：一个数和它的相反数相等。很显然，a =0。
【知识点4】绝对值
几何定义：一般地，数轴上表示数a的点与原点的距离叫做数a的绝对值，记作|a|。
代数定义：一个正数的绝对值是它本身；一个负数的绝对值是它的相反数；0的绝对值是0。
即：如果a >0，那么|a|=a； 如果a =0，那么|a|=0；如果a <0，那么|a|=-a。
a =|a|所表示的意义是：一个数和它的绝对值相等。很显然，a≥0。
【知识点5】倒数
定义：乘积是1的两个数互为倒数。即：如果a与b互为倒数，则有ab=1，反之亦成立。
所表示的意义是：一个数和它的倒数相等。很显然，a =±1。
【知识点6】数的大小比较
法则：正数大于0，0大于负数，正数大于负数；两个负数，绝对值大的反而小。

题型01：正数与负数
1. （2023春•南岗区校级期中）检测4个足球，其中质量超过标准的克数记为正数，不足的克数记为负数．从轻重的角度看，最接近标准的是　　
A． B． C． D．
【分析】由已知和要求，只要求出超过标准的克数和低于标准的克数的绝对值，绝对值小的则是最接近标准的球．
【解答】解：通过求4个排球的绝对值得：
，，，，
的绝对值最小．
所以这个球是最接近标准的球．
故选：．
2. （2023春•黄浦区期中）若收入2008元记为元，则支出168.2元应记为 　 　元．
【分析】根据正负数的意义解答即可．
【解答】解：因为收入2008元记为元，则支出168.2元应记为元．
故答案为：．
3. （2023春•鼓楼区校级期中）如果水位升高2米时水位变化记作，那么水位下降2米时水位变化记作 　 　．
【分析】根据正负数的意义即可求出答案．
【解答】解：如果水位升高时，水位变化记作，那么水位下降时，水位变化记作．
故答案为：．
4. （2023春•闵行区期中）六年级某班三位任课老师中，如果语文老师的岁数比数学老师大3岁记作3岁，那么英语老师的岁数比数学老师小5岁，可以记作 　 　岁．
【分析】根据正数和负数的意义解答即可．
【解答】解：如果语文老师的岁数比数学老师大3岁记作3岁，那么英语老师的岁数比数学老师小5岁，可以记作岁．
故答案为：．

题型02：有理数
5. （2023春•闵行区期中）有理数分为　　
A．正数和负数 B．素数和合数 C．整数和分数 D．偶数和奇数
【分析】根据有理数的分类解答即可．
【解答】解：有理数分为整数和分数．
故选：．
6. （2023春•闵行区期中）在，，，0，7.6，2，，．这八个有理数中非负数有　　
A．4个 B．5个 C．6个 D．7个
【分析】根据有理数的分类得到在所给数中非负数为，0，7.6，2，．
【解答】解：在，，，0，7.6，2，，．这八个数中，
非负数为，0，7.6，2，，有5个．
故选：．
7. （2022秋•蓝山县期中）下列说法正确的是　　
A．整数包括正整数和负整数
B．分数包括正分数、负分数和零
C．表示一个负数
D．零是整数，但不是正数也不是负数
【分析】根据有理数的分类及负数的定义进行判断即可．
【解答】解：．整数包括正整数，0和负整数，
则不符合题意；
．分数包括正分数和负分数，
则不符合题意；
．当时，，
则不符合题意；
．零是整数，但它不是正数也不是负数，
则符合题意；
故选：．
8. （2022秋•魏县期中）与相等的是　　
A． B． C． D．
【分析】根据有理数的加减法则进行计算即可．
【解答】解：、，符合题意；
、，不符合题意；
、，不符合题意；
、，不符合题意．
故选：．

题型03：数轴
9. （2023春•仓山区校级期中）如图，数轴上点表示的数可能是　　

A． B． C． D．3.3
【分析】观察点在数轴上的位置，再作判断即可．
【解答】解：点在和之间，且偏一侧，所以符合题意的数是，
故选：．
10. （2023春•临清市期中）如图，数轴上的点与点所表示的数分别为，，则下列不等式不成立是　　

A． B． C． D．
【分析】通过图象可知，，根据不等式的性质判断即可．
【解答】解：根据题干可以确定是选择“不成立”的选项，
．，因不等式左右两边同乘，不等号符号应该发生改变，故不成立，选．
．，因不等式左右两边同加3，不等号不发生变化，故成立．
，因不等式左右两边同乘，不等号不发生变化，故成立．
．，因不等式左右两边同时减去同一个数，不等号不发生变化，故成立．
故选：．
11. （2023春•建阳区期中）如图，把半径为1的圆放到数轴上，圆上一点与表示1的点重合，圆沿着数轴正方向滚动一周，此时点表示的数是　　

A． B． C． D．
【分析】首先计算出圆的周长，然后可得答案．
【解答】解：圆的半径为1，
圆的周长为：，
点与表示1的点重合，
圆沿着数轴正方向滚动一周，此时点表示的数是，
故选：．
12. （2023春•宁江区期中）如图，数轴上表示的点到原点的距离是　　

A． B．2 C． D．
【分析】根据绝对值的定义即可得到结论．
【解答】解：数轴上表示的点到原点的距离是2，
故选：．

题型04：数轴的动态问题
13. （2022秋•邗江区期中）在一条可以折叠的数轴上，，表示的数分别是，9，如图，以点为折点，将此数轴向右对折，若点在点的右边，且，则点表示的数是 　 　．

【分析】根据与表示的数求出的长，再由折叠后的长，求出的长，即可确定出表示的数．
【解答】解：，表示的数为，9，
，
折叠后，
，
点在的左侧，
点表示的数为．
故答案为：．
14. （2023春•德惠市期中）如图，已知点在数轴上对应的数为，点对应的数比点大12，与之间的距离记作．

（1）则点表示的数是 　 　；
（2）在、之间有一点，设点在数轴上对应的数为，当时，求的值．
【分析】（1）根据已知条件列出算式计算即可求解；
（2）根据等量关系得到方程，解方程即可求解．
【解答】解：（1），
故点表示的数是 10；
故答案为：10；
（2）依题意有，
解得，
答：的值为6．
15. （2022秋•灞桥区校级期中）如图，有两条线段，（单位长度），（单位长度）在数轴上，点在数轴上表示的数是，点在数轴上表示的数是15．
（1）点在数轴上表示的数是 　 　，点在数轴上表示的数是 　 　；
（2）若线段以1个单位长度秒的速度向左匀速运动，同时线段以2个单位长度秒的速度也向左匀速运动，设运动时间为秒，当为何值时，点与点之间的距离为1个单位长度？
（3）若线段、线段分别以1个单位长度秒、2个单位长度秒的速度同时向左匀速运动，与此同时，动点从出发，以4个单位长度秒的速度向右匀速运动．设运动时间为秒，当时，的值是否发生变化？若不变化，求出这个定值，若变化，请说明理由．


【分析】（1）由已知直接可得答案；
（2）求出运动后表示的数是，运动后表示的，根据点与点之间的距离为1个单位长度列方程可解得答案；
（3）求出运动后表示的数是，运动后表示的数是，运动后表示的数是，运动后表示的数是，从而可表示出，，代入计算即可得到答案．
【解答】解：（1），，
点在数轴上表示的数是，点在数轴上表示的数是14，
故答案为：，14；
（2）根据题意，运动后表示的数是，运动后表示的，
，
解得或，
当为25或23时，点与点之间的距离为1个单位长度；
（3）的值不发生变化，理由如下：
根据题意，运动后表示的数是，运动后表示的数是，运动后表示的数是，运动后表示的数是，
，
，，
，
为定值，这个定值是42．
16. （2022秋•蓝山县期中）已知数轴上三点、、对应的数分别是，1，4，点为数轴上任意一点，且表示的数是．

（1）点到点的距离为多少个单位长度？
（2）点到的距离可以表示为 　 　；
（3）如果点到点和到点的距离相等，那么的值是多少？
（4）数轴上是否存在点，使点到点与到点的距离之和是8？若存在，请直接写出的值；若不存在，请说明理由．
【分析】（1）根据数轴上两点之间距离的计算方法进行计算即可；
（2）根据绝对值的几何意义即可得出答案；
（3）根据，列方程求解即可；
（4）根据，即，求解即可．
【解答】解：（1），
答：；
（2）点到的距离可以表示为，
故答案为：；
（3）由题意得，，即，
解得，
答：当时，点到点和到点的距离相等；
（4）由题意得，，
即，
当时，，
解得；
当时，，
解得；
答：当点到点与到点的距离之和是8，点所表示的数是或．

题型05：相反数
17. （2023春•罗源县校级期中）的相反数是　　
A．2 B． C． D．
【分析】利用相反数的定义判断即可．
【解答】解：的相反数是2．
故选：．
18. （2023春•柯桥区期中）的相反数是　　
A． B． C． D．2023
【分析】只有符号不同的两个数叫做互为相反数，由此即可得到答案．
【解答】解：的相反数为2023．
故选：．
19. （2023春•南岗区校级期中）的相反数是　　
A． B．3 C． D．
【分析】只有符号不同的两个数叫做互为相反数，由此即可得到答案．
【解答】解：的相反数是．
故选：．
20. （2023春•马边县期中）的相反数是 　 　．
【分析】根据互为相反数的两数之和为0，进行求解即可．
【解答】解：的相反数是，
故答案为：．

题型06：绝对值
21. （2023春•西丰县期中）的绝对值是　　
A． B． C． D．
【分析】根据绝对值的定义进行计算即可．
【解答】解：，
故选：．
22. （2023春•金昌期中）的绝对值是　　
A． B．9 C． D．
【分析】根据绝对值的性质：一个负数的绝对值是它的相反数即可得出答案．
【解答】解：根据绝对值的性质，得．
故选：．
23. （2023春•章贡区期中）的绝对值是　　
A． B． C． D．2023
【分析】根据绝对值的定义进行计算即可．
【解答】解：，
故选：．
24. （2023春•沙坪坝区校级期中）若一个数的绝对值是，则这个数是　　
A． B． C．或 D．或
【分析】根据绝对值等于一个正数的数有两个解决此问题．
【解答】解：一个数的绝对值是，则这个数是，
故选：．

题型07：绝对值化简
25. （2022秋•和平区校级期中）当，，且，则的值为　　
A． B．或 C．2 D．
【分析】先根据绝对值的性质，判断出、的大致取值，然后根据，进一步确定、的值，再代入求解即可．
【解答】解：，，
，
，
，
．，
当，时，；
当，时，；
故的值为或．
故选：．
26. （2022秋•双流区期中）若，则的取值范围是　　
A． B． C． D．
【分析】根据绝对值的意义得到，然后解不等式即可．
【解答】解：，
，
．
故选：．
27. （2023春•松江区期中）如果，化简：　 　．
【分析】根据去绝对值法则去掉绝对值．然后合并同类项化简即可．
【解答】解：，
，
，
，
，
，
原式，
故答案为1．
28. （2022秋•红安县期中）有理数，，在数轴上表示的点如图所示，化简　 　．

【分析】根据图形判断、、的符号，以及绝对值中三个式子的符号，再去绝对值化简．
【解答】解：根据数轴可知，，且，
故，，，
，，，
原式

．
故答案为：．

题型08：绝对值的非负性
29. （2023春•南召县期中）若与的值互为相反数，则的值为　　
A．11 B．3 C．10 D．
【分析】直接利用非负数的性质得出，，，进而利用整体思想得出答案．
【解答】解：与的值互为相反数，，，，，
，
①②得：
，
故．
故选：．
30. （2022秋•南山区校级期中）若有理数，满足，则的值为　　
A．5 B．6 C．7 D．8
【分析】根据绝对值的非负性，求出，，再代入计算即可．
【解答】解：由题意得，，，
解得：，，
则，
故选：．
31. （2022秋•南开区期中）若，则　 　．
【分析】先根据非负数的性质求出，的值，再由有理数的乘法法则解答即可．
【解答】解：，
，，解得，，
．
故答案为：．
32. （2022秋•大石桥市期中）已知与互为相反数，则　 　．
【分析】根据非负数的性质得出，的值，再代入计算即可．
【解答】解：与互为相反数，
，
，，
，
，
故答案为：．

题型09：有理数比较大小
33. （2022秋•龙口市期中）在，，3，0这四个数中，最小的数是　　
A． B． C．3 D．0
【分析】正数大于0，负数小于0，正数大于负数，两个负数比较大小，绝对值大的反而小．
【解答】解：，
最小的数是．
故选：．
34. （2023春•襄州区期中）在0，，1，这四个数中，最小的数是　　
A．0 B． C．1 D．
【分析】根据有理数的大小得出结论即可．
【解答】解：，
故选：．
35. （2023春•长沙期中）下列选项中，最小的数是　　
A．1 B． C．0 D．
【分析】根据实数大小的比较方法，比较大小即可．
【解答】解：，
，
故选：．
36. （2022秋•鹤峰县期中）下列各数中，最大的是　　
A． B． C． D．
【分析】根据有理数的大小比较即可求出答案．
【解答】解：，
故选：．


1. （2022秋•温州期中）下列各数中最小的数是　　
A． B．0 C． D．3
【分析】依据比较有理数大小的法则进行判断即可．
【解答】解：，
最小的数是．
故选：．
2. （2023春•蓬安县期中）在0，，1，四个数中，最小的数是　　
A．0 B． C．1 D．
【分析】有理数大小比较的法则：①正数都大于0；②负数都小于0；③正数大于一切负数；④两个负数，绝对值大的其值反而小，据此判断即可．
【解答】解：，
在0，，1，四个数中，最小的数是．
故选：．
3. （2023春•南宁期中）2023的相反数是　　
A．2023 B． C． D．
【分析】只有符号不同的两个数叫做互为相反数，由此即可得到答案．
【解答】解：2023的相反数是．
故选：．
4. （2023春•永春县校级期中）的相反数是　　
A．2023 B． C． D．
【分析】根据“只有符号不同的两个数叫做互为相反数”解答．
【解答】解：的相反数是，
故选：．
5. （2022秋•镇海区校级期中）在，，，0，中，有理数有　　个．
A．1 B．2 C．3 D．4
【分析】根据有理数的分类即可判断．
【解答】解：有理数有：，，0，共3个，
故选：．
6. （2022春•梁平区期中）在，，0，这四个数中，属于负整数的是　　
A． B． C．0 D．
【分析】根据实数分类的相关概念，可辨别此题结果．
【解答】解：，都是分数，
选项，不符合题意；
既不是正数，也不是负数，
选项不符合题意；
是负整数，
选项符合题意，
故选：．
7. （2022秋•越城区期中）如图，将一刻度尺放在数轴上（数轴1个单位长度是，刻度尺上对应数轴上的数3，那么刻度尺上对应数轴上的数为　　

A． B． C． D．
【分析】利用两点间的距离，求得刻度尺上的点到原点的距离即可．
【解答】解：刻度尺上的对应数轴上的3，
刻度尺上对应的数到3的距离也是，
到原点的距离是，
在原点左侧，
对应的数是．
故选：．
8. （2022秋•宁陕县校级期中）在数轴上表示与5的点距离5个单位长度的数是　　
A．0 B．10 C．0或10 D．5
【分析】分为两种情况，一种是该点在表示5的点的左侧，另一种是该点在表示5的点的右侧，分别求出即可选择．
【解答】解：当该点在表示5的点的左侧时，
该数为：，
当该点在表示5的点的右侧时，
该数为：，
该点表示的数为0或10，
故选：．
9. （2022秋•桐乡市期中）数轴上点，，分别表示数，，，下列说法正确的是　　
A．点一定在点的右边 B．点一定在点的左边
C．点一定在点的右边 D．点一定在点的左边
【分析】由于不知道数的数值，所以不清楚点与点，点与点的位置关系，再根据点，分别表示数，即可判断．
【解答】解：的数值未知，
点与点，点与点的位置关系未知，
点，分别表示数，，
即点向左移动一个单位，
点一定在点的左边，
故选：．
10. （2022秋•通州区期中）数轴上点表示的数为，与点距离为4个单位长度的点表示的数为　　
A．1 B． C．1或 D．1或7
【分析】求出比大4和比小4的数即可．
【解答】解：，，
与点距离为4个单位长度的点表示的数为1或，
故选：．
11. （2023春•荔城区校级期中）如图，把半径为0.5的圆放到数轴上，圆上一点与表示1的点重合，圆沿着数轴滚动一周，此时点表示的数是　　

A．或 B．或 C．或 D．或
【分析】根据半径为0.5的圆从数轴上表示1的点沿着数轴滚动一周，滚动的距离就是圆的周长，再由圆的周长公式得出周长为，分两种情况，即可得答案．
【解答】解：由半径为0.5的圆从数轴上表示1的点沿着数轴滚动一周到达点，
故滚动一周后点与1之间的距离是，
故当点在1的左边时表示的数是，
当点在1的右边时表示的数是．
故选：．
12. （2023春•鼓楼区校级期中）如图，数轴上，两点对应的数分别为，2，若数轴上的点满足，则点表示的数为 　 　．

【分析】分两种情况进行讨论：①点在点的左侧；②点在点的右侧，再根据所给的条件进行求解即可．
【解答】解：设点所表示的数为，
①当点在点的左侧时，
，
，
解得：；
②点在点的右侧时，
，
，
解得：，
综上所述，点表示的数为或3．
故答案为：或3．
13. （2023春•应城市期中）如图，把一个直径为1个单位长度的圆片上的点放在表示的点处，并把圆片沿数轴正方向无滑动地滚动1周，点到达点的位置，则点表示的数是 　 　．

【分析】先求出圆的周长，再根据数轴的特点进行解答即可．
【解答】解：圆的直径为1个单位长度，
此圆的周长，
当圆向右滚动时点表示的数是．
故答案为：．
14. （2023春•香坊区校级期中）一个月内，小明体重减小，这个月小明的体重增加　 　．
【分析】增加和减少具有相反意义，根据正负数可以表示一对具有相反意义的量即可求解．
【解答】解：一个月内，小明体重减小，这个月小明的体重增加．
故答案为：．
15. （2023春•芝罘区期中）如图，数轴上有、、三点，、两点表示的有理数是分别是和8，若将该数轴从点处折叠后，点和点恰好重合，那么点表示的有理数是 　 　．

【分析】由题意得点是线段的中点，再进行求解．
【解答】解：由题意得点是线段的中点，
点表示的有理数是：


，
故答案为：3．
16. （2022春•南岗区校级期中）若数轴上、两点对应的数分别为、4，为数轴上一点，对应数为．
（1）若为线段的三等分点，直接写出点对应的数．

（2）数轴上是否存在点，使点到点、点的距离和为11？若存在，求出值；若不存在，请说明理由．
（3）若点从点出发向右运动，速度是2个单位分，点从点出发向左运动，速度是3个单位分，它们同时出发，经过几分钟，、、三点中，其中一点是另外两点连成线段的中点？
【分析】（1）根据题意可得，再分两种情况：当时，当时，即可求解；
（2）根据题意可得点不在，两点之间，再分两种情况：当点在点的左侧时，当点在点的右侧时，列出方程，即可求解；
（3）根据题意可得当时，点，两点相遇；当时，点到达点，当时；点到达点；设经过分钟，、、三点中，其中一点是另外两点连成线段的中点，再分三种情况：当时，点在点，之间，此时，当时，，当时，此时，列出方程，即可求解．
【解答】解：（1）根据题意得：，
当时，，
点对应的数为，
点对应的数为；
当时，，
点对应的数为4，
点对应的数为1；
综上所述，点对应的数为或1；
（2）存在，
，点到点、点的距离和为11，
点不在，两点之间，
当点在点的左侧时，，
解得：；
当点在点的右侧时，，
解得：；
综上所述，的值为或5；
（3）（分，（3分），（分，
当时，点，两点相遇；当时，点到达点，当时；点到达点；
设经过分钟，、、三点中，其中一点是另外两点连成线段的中点，
当时，点在点，之间，此时，
，解得：，
当时，，
，
解得：；
当时，，
，
解得：（不符合题意，舍去）；
综上所述，它们同时出发，经过或分钟，、、三点中，其中一点是另外两点连成线段的中点．
17. （2023春•南岗区期中）某自行车厂一周计划生产700辆自行车，平均每天生产100辆，由于各种原因实际每天生产量与计划量相比有出入．下表是某周的生产情况（超产为正、减产为负）
星期
一
二
三
四
五
六
日
增减







（1）根据记录可知前四天共生产 　 　辆；
（2）产量最多的一天比产量最少的一天多生产 　 　辆；
（3）该厂实行计件工资制，每周生产一辆自行车给工人60元，超额完成任务超额部分每辆再奖15元，少生产一辆扣20元，那么该厂工人这一周的工资总额是多少元？
【分析】（1）根据有理数的加法，可得答案；
（2）根据有理数的减法，可得答案；
（3）根据有理数的乘法，可得工资与奖金，根据有理数的加法，可得答案．
【解答】解：（1）（辆；
（2）产量最多的一天比产量最少的一天多生产；
故答案为：412，26；
（3）根据图表信息，本周生产的车辆共计：．
（元．
答：该厂工人这一周的工资总额是42675元．
18. （2022秋•南山区校级期中）学习完数轴以后，喜欢探索的小聪在纸上画了一个数轴（如图所示），并进行下列操作探究：
（1）操作一：折叠纸面，使表示1的点与表示的点重合，则表示的点与表示 　 　的点重合．
操作二：折叠纸面，使表示的点与表示1的点重合，回答以下问题：
（2）表示2的点与表示 　　 的点重合；
（3）若数轴上、两点之间距离是在的左侧），且折叠后、两点重合．求、两点表示的数是多少？

【分析】（1）直接利用已知得出中点进而得出答案；
（2）利用表示的点与1表示的点重合得出中点，进而得出答案；
（3）利用数轴再结合、两点之间距离为，即可得出两点表示的数．
【解答】解：（1）折叠纸面，使1表示的点与表示的点重合，则对称中点是0，
表示的点与表示4的点重合．
故答案为：4；
（2）折叠纸面，使表示的点与1表示的点重合，
对称中点是数表示的点，
表示的点与数表示的点重合．
故答案为：；
（3）由（2）可知：对称中点是数表示的点
数轴上，两点经折叠后重合，
数轴上点与数表示的点的距离等于数轴上点与数表示的点的距离，
数轴上、两点之间的距离为，其中在的左侧，
对折后长度为
表示的数是，表示的数是．
故答案为：，．
19. （2022秋•天门期中）如图，已知数轴上点表示的数为6，是数轴上在左侧的一点，且，两点间的距离为10．动点从点出发，以每秒6个单位长度的速度沿数轴向左匀速运动，设运动时间为秒．
（1）数轴上点表示的数是　 　，点表示的数是　 　（用含的代数式表示）；
（2）动点从点出发，以每秒4个单位长度的速度沿数轴向左匀速运动，若点、同时出发．求：
①当点运动多少秒时，点与点相遇？
②当点运动多少秒时，点与点间的距离为8个单位长度？

【分析】（1）由已知得，则，因为点在原点左边，从而写出数轴上点所表示的数；动点从点出发，运动时间为秒，所以运动的单位长度为，因为沿数轴向左匀速运动，所以点所表示的数是；
（2）①点运动秒时追上点，由于点要多运动10个单位才能追上点，则，然后解方程得到；
②分两种情况：当点运动秒时，不超过，则；超过，则；由此求得答案解即可．
【解答】解：（1）数轴上点表示的数为6，
，
则，
点在原点左边，
数轴上点所表示的数为；
点运动秒的长度为，
动点从点出发，以每秒6个单位长度的速度沿数轴向左匀速运动，
所表示的数为：；
（2）①点运动秒时追上点，
根据题意得，
解得，
答：当点运动5秒时，点与点相遇；
②设当点运动秒时，点与点间的距离为8个单位长度，
当不超过，则，解得；
当超过，则，解得；
答：当点运动1或9秒时，点与点间的距离为8个单位长度．