【期中真题】北京市中国人民大学附属中学2021-2022学年高一上学期期中练习数学试题.zip

这是一份【期中真题】北京市中国人民大学附属中学2021-2022学年高一上学期期中练习数学试题.zip，文件包含期中真题北京市中国人民大学附属中学2021-2022学年高一上学期期中练习数学试题原卷版docx、期中真题北京市中国人民大学附属中学2021-2022学年高一上学期期中练习数学试题解析版docx等2份试卷配套教学资源，其中试卷共22页， 欢迎下载使用。
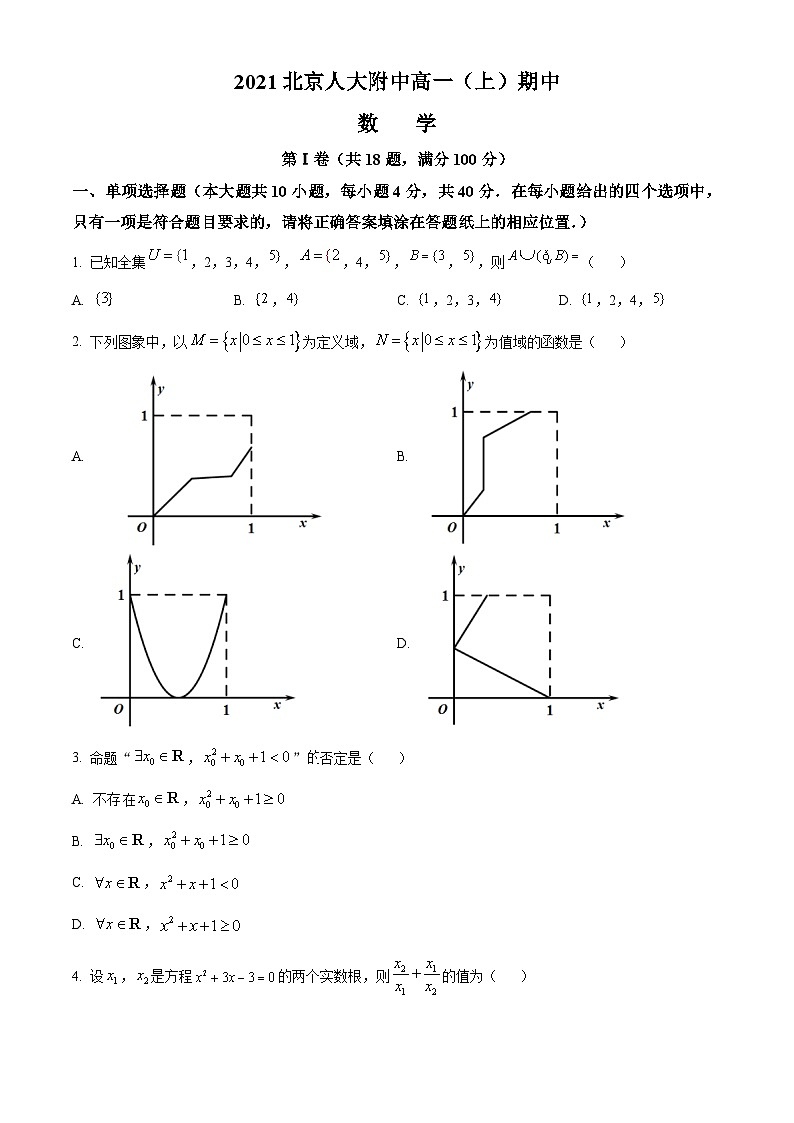
2021北京人大附中高一（上）期中数    学第Ⅰ卷（共18题，满分100分）一、单项选择题（本大题共10小题，每小题4分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的，请将正确答案填涂在答题纸上的相应位置．）1. 已知全集，2，3，4，，，4，，，，则（    ）A.  B. ， C. ，2，3， D. ，2，4，2. 下列图象中，以为定义域，为值域的函数是（    ）A.  B. C.  D. 3. 命题“，”否定是（    ）A. 不存，B. ，C. ，D. ，4. 设，是方程的两个实数根，则的值为（    ）A. 5 B.  C. 1 D. 5. 不等式的解集为（    ）A.  B. C  D. 6. 设函数，则下列结论正确的是（    ）A. 的值域为 B. C. 是偶函数 D. 是单调函数7. 在下列各组函数中，与表示同一函数的是（    ）A ， B. ，C. ， D. ，8. “”是“”的（    ）A. 充分不必要条件 B. 充要条件C. 必要不充分条件 D. 既不充分也不必要条件9. 在用“二分法”求函数零点近似值时，第一次所取的区间是，则第三次所取的区间可能是（    ）A.  B.  C.  D. 10. 张老师国庆期间驾驶电动车错峰出行，并记录了两次“行车数据”，如表：记录时间累计里程（单位：公里）平均耗电量（单位：公里）剩余续航里程（单位：公里）2021年10月2日20000.125380 2021年10月3日22000.124166（注：累计里程指汽车从出厂开始累计行驶的路程，累计耗电数指汽车从出厂开始累计消耗的电量，平均耗电量，剩余续航里程，下面对该车在两次记录时间段内行驶1公里的耗电量（单位：公里）估计正确的是（    ）A. 0.104 B. 0.114 C. 0.118 D. 0.124二、填空题（本大题共5小题，每小题5分，共25分．请把结果填在答题纸上的相应位置．）11. 函数的定义域为_____________.12. 满足的集合的个数为____________个.13. 设，，若是的充分不必要条件，则实数的取值范围是 __；若是的必要不充分条件，则实数的取值范围是 __．14. 已知函数在上单调递增，则实数的取值范围为_______.15. 已知定义在非零实数上的奇函数，满足，则等于______.三、解答题（本大题共3小题，共35分，解答应写出文字说明过程或演算步骤，请将答案'写在答题纸上的相应位置．）16. 已知全集，非空集合A，B满足，.（1）当，求；（2）若，求实数a的取值范围.17. 已知函数且.（1）判断并证明函数在其定义域上的奇偶性；（2）证明函数在上是增函数.18. 已知函数（其中）.（1）当时，画出函数的图象，并写出函数的单调递减区间；（2）若在区间上的最大值为，求的表达式.第Ⅱ卷（共18题，满分50分）一、选择题（共3小题，每小题3分，共18分．在每小题给出的四个选项中，只有一项是符合题目要求的，请将所有正确答案填涂在答题纸上的相应位置．19. 已知实数a，b，c满足b＋c＝6－4a＋3a2，c－b＝4－4a＋a2，则a，b，c的大小关系是（    ）A. c≥b>a B. a>c≥bC. c>b>a D. a>c>b20. 《几何原本》中的几何代数法(以几何方法研究代数问题)成为了后世数学家处理问题的重要依据.通过这一原理，很多的代数的公理或定理都能够通过图形实现证明，也称之为无字证明.如图所示的图形，在AB上取一点，使得，，过点作交圆周于D，连接OD.作交OD于.则下列不等式可以表示的是（    ）A.  B. C.  D. 21. 已知函数是定义在上的偶函数，，当时，，则不等式的解集是A.  B.  C.  D. 二、填空题（共3小题，每小题6分，共18分．请把结果填在答题纸上的相应位置．）22. 已知函数，则______.23. 函数(a>0)，在区间[，t+1](t∈R)上函数的最大值为M，最小值为N．当t取任意实数时，MN的最小值为2，则a=________.24. 若不等式对一切恒成立，则实数x的取值范围是______.三、解答题（本小题14分．解答应写出文字说明过方或演算步骤，请将答案写在答题纸上的相应位置．）25. 已知集合，对于A的子集S若存在不大于的正整数，使得对于S中的任意一对元素、，都有，则称具有性质.（1）当时，判断集合和是否具有性质P？并说明理由；（2）若时，①如果集合S具有性质P，那么集合是否一定具有性质P？并说明理由；②如果集合S具有性质P，求集合S中元素个数最大值.