【期中真题】天津市南开中学2022-2023学年高一上学期阶段性质量检测(一)数学试题.zip

高一年级数学阶段性质量检测（一）

一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的．本大题共9小题，每小题4分，共36分．

1. 设集合，，，则（    ）

A.  B.  C.  D.

2. 已知幂函数的图象经过点，则（    ）

A  B. 3 C.  D.

3. 命题：“对任意的，”的否定是（    ）

A. 不存在， B. 存在，

C. 存在， D. 对任意的，

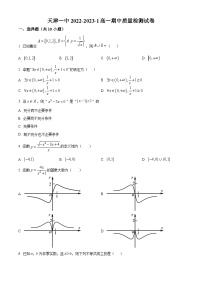
4. 若函数的定义域为，值域为，则的图象可能是（    ）

A.  B.

C.  D.

5. 若，则下列不等式一定成立的是（    ）

A.  B.

C.  D.

6. 已知，，则（    ）

A.  B.  C.  D.

7. 使不等式成立的一个充分不必要条件是（    ）

A.  B.

C.  D.

8. 已知函数，，若，则的取值范围是（    ）

A.  B.

C.  D.

9. 已知函数是定义在R上的函数，其中是奇函数，是偶函数，且，若对于任意，都有，则实数的取值范围是（    ）

A.  B.  C.  D.

二、填空题：本大题共6小题，每小题4分，共24分．

10. 函数的定义域为________．

11 函数，则________．

12. 已知集合，，则集合中的元素个数为________．

13. 函数的值域是________．

14. 某公司一年购买某种货物吨，每次购买吨，运费为万元/次，一年总存储费用为万元．要使一年的总运费与总存储费用之和最小，则的值是________．

15. 若函数在上是减函数，则实数的取值范围为______________.

三、解答题：本大题共3小题，16题12分，17，18题每题14分，共40分．

16. 已知函数的定义域为，集合，．

（1）求；

（2）若，求实数的取值范围．

17. 已知.

（1）当时，解关于的不等式；

（2）当时，解关于不等式.

18. 已知是定义域为的奇函数．当时，．

（1）求函数的解析式；

（2）当时，设函数，判断在上单调性，并用定义加以证明；

（3）设，当时，的取值范围为，求实数的值．