2023-2024学年贵州省遵义十二中九年级（上）第一次月考数学试卷(含解析)

这是一份2023-2024学年贵州省遵义十二中九年级（上）第一次月考数学试卷(含解析)，共11页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1．下列属于一元二次方程的是（ ）
A．x2﹣3x+y＝0B．x
C．x2+5x＝0D．x（x2﹣4x）＝3
2．随着贵州“村超”的火爆出圈，黔东南州榕江县搭乘“村超”快车，“超级星期六足球之夜”品牌价值日益彰显，旅游业持续升温．据初步测算，榕江县已累计接待游客50万人次，实现旅游综合收入12.41亿元这个数据用科学记数法表示为（ ）
A．12.41×108元B．1.241×109元
C．1.241×1010元D．1.241×108元
3．把一元二次方程（x﹣1）2＝3x﹣2化为一般形式，若二次项系数是1，则一次项系数和常数项分别为（ ）
A．﹣3 和3B．﹣3 和1C．﹣5 和3D．﹣5 和1
4．用配方法解一元二次方程x2﹣4x﹣2＝0的过程中，配方正确的是（ ）
A．（x+2）2＝2B．（x﹣2）2＝2C．（x+2）2＝6D．（x﹣2）2＝6
5．如果a是一元二次方程2x2＝6x﹣4的根，则代数式a2﹣3a+2024的值为（ ）
A．2021B．2022C．2023D．2024
6．若方程ax2+bx+c＝0（a≠0），a、b、c满足a+b+c＝0和a﹣b+c＝0，则方程的根是（ ）
A．1，0B．﹣1，0C．1，﹣1D．无法确定
7．如图，一块长16m，宽8m的矩形菜地，现要在中间铺设同样宽度的石子路，余下的部分用于种植，且种植面积为105m2．设石子路的宽度为xm，则下面所列方程正确的是（ ）
A．（16﹣x）（8﹣x）+x2＝105
B．（16﹣x）（8﹣x）＝105
C．（16﹣2x）（8﹣x）+x2＝105
D．（16﹣2x）（8﹣x）＝105
8．函数y＝自变量x的取值范围是（ ）
A．x≥﹣1B．x≠2C．x≥﹣1且x≠2D．﹣1≤x＜2
9．若关于x的一元二次方程kx2+2x﹣1＝0有实数根，则k的取值范围是（ ）
A．k≥﹣1且k≠0B．k≥﹣1C．k＞﹣1D．k＞﹣1且k≠0
10．新冠肺炎奥密克戎变异株BA.5自2021年底出现后，目前已成为全球流行的变异株，更是近期深圳感染的主要毒株，潜伏期更短，传播力更强，传播速度更快．变异株2分钟左右进入宿主细胞，20﹣30分钟左右呈现指数复制，12﹣24小时后释放成熟的病毒颗粒，通过气溶胶等方式进行传播．若有两个人患了该新冠肺炎，经过两轮传播后共有338个人被传染，那么每轮传染中平均一个人传染几个人（ ）
A．13B．11C．12D．14
11．等腰三角形一边长为2，它的另外两条边的长度是关于x的一元二次方程x2﹣6x+k＝0的两个实数根，则k的值是（ ）
A．8B．9C．8或9D．12
12．如图1，矩形ABCD中，点E为BC的中点，点P沿BC从点B运动到点C，设B，P两点间的距离为x，PA﹣PE＝y，图2是点P运动时y随x变化的关系图象，则BC的长为（ ）
A．6B．7C．8D．9
二、填空题（本题共4小题，每小题4分，共16分）
13．方程（x+2）2＝8，则方程的根为 ．
14．若方程是关于x的一元二次方程，则a的值为 ．
15．一个两位数，十位上的数字比个位上的数字的平方少9．如果把十位上的数字与个位上的数字对调，得到的两位数比原来的两位数小27，则原来的两位数是 ．
16．已知：m2﹣2m﹣1＝0，n2+2n﹣1＝0且mn≠1，则的值为 ．
三、解答题（本题共9小题，共98分）
17．计算题：
（1）；
（2）解方程：（3﹣y）2+y2＝12．
18．先化简，再求值：÷（m+3+），其中m是方程x2﹣2x﹣1＝0的根．
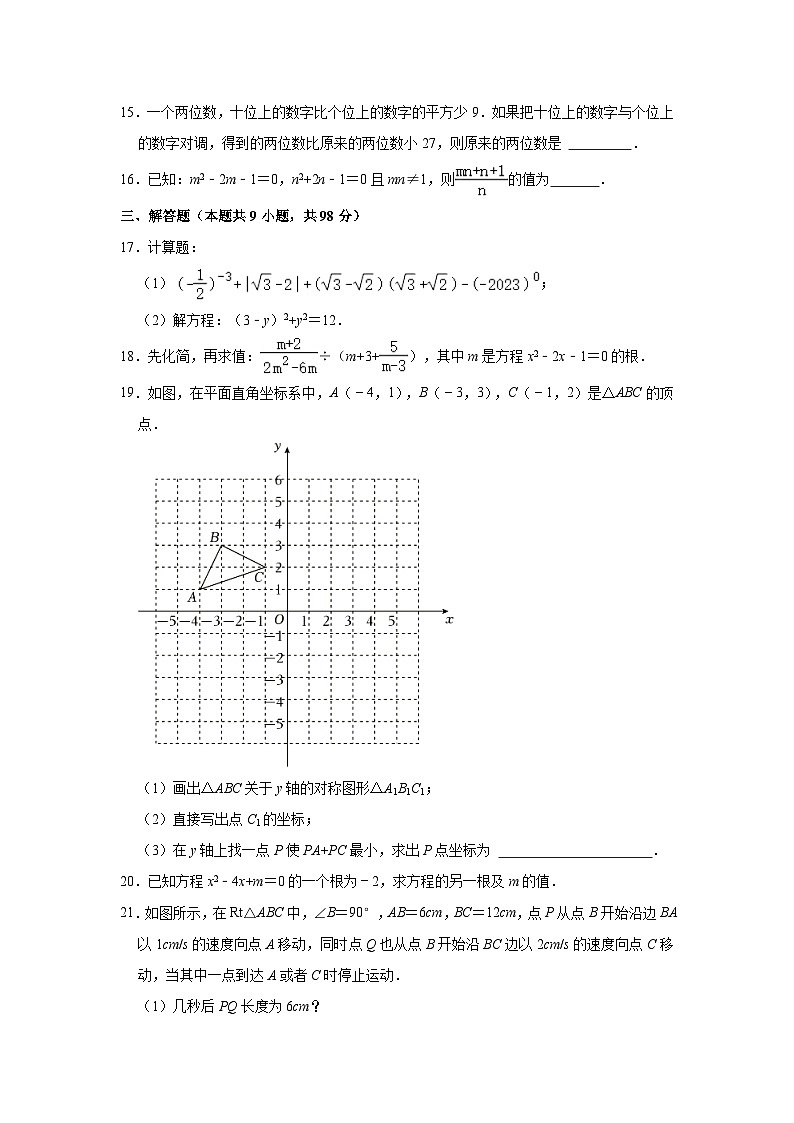
19．如图，在平面直角坐标系中，A（﹣4，1），B（﹣3，3），C（﹣1，2）是△ABC的顶点．
（1）画出△ABC关于y轴的对称图形△A1B1C1；
（2）直接写出点C1的坐标；
（3）在y轴上找一点P使PA+PC最小，求出P点坐标为 ．
20．已知方程x2﹣4x+m＝0的一个根为﹣2，求方程的另一根及m的值．
21．如图所示，在Rt△ABC中，∠B＝90°，AB＝6cm，BC＝12cm，点P从点B开始沿边BA以1cm/s的速度向点A移动，同时点Q也从点B开始沿BC边以2cm/s的速度向点C移动，当其中一点到达A或者C时停止运动．
（1）几秒后PQ长度为6cm？
（2）几秒后△PBQ的面积是24平方厘米？
22．已知关于x的一元二次方程x2+（2k+1）x+k2+k＝0（k为常数）．
（1）求证：无论k取何值，方程都有两个不相等的实数根；
（2）若方程的两个实数根x1，x2满足x1+x2＝x1•x2﹣1，求k的值．
23．某扶贫单位为了提高贫困户的经济收入，购买了39m的铁栅栏，准备用这些铁栅栏为贫困户靠墙（墙长15m）围建一个中间带有铁栅栏的矩形养鸡场（如图所示）．
（1）若要建的矩形养鸡场面积为120m2，求鸡场的长AB和宽BC；
（2）该扶贫单位想要建一个130m2的矩形养鸡场，这一想法能实现吗？请说明理由．
24．“小龙虾”是我县特色农业的拳头产品，在南县被广泛养殖．2020年估计某村养殖面积有100亩，到2022年该村养殖面积达到196亩．
（1）求该村这两年“小龙虾”养殖面积的平均增长率；
（2）某养殖户调查发现，当“小龙虾”的售价为20元/千克时，每天能售出200千克，售价每降价1元，每天可多售出50千克．为了推广宣传，该养殖户决定降价促销，同时减少存量，已知“小龙虾”的平均成本为12元/千克，若要确保每天获利1750元，则售价应该降低多少元？
25．如图①，在△ABC中，AD⊥BC于D，BC＝14，AD＝8，BD＝6，点E是AD上一动点（不与点A，D重合），在△ADC内作矩形EFGH，点F在DC上，点G、H在AC上，设DE＝x，连接BE．
（1）设矩形EFGH的面积为S1，△ABE的面积为S2，令y＝，求y关于x的函数解析式；（要求写出自变量的取值范围）
（2）如图②，点M是（1）中得到的函数图象上的任意一点，N的坐标为（2，0），当△OMN为等腰三角形时，求点M的坐标．
​
参考答案
一、选择题（本大题共12个小题，每小题3分，共36分.在每个小题给出的四个选项中，只有一项符合题目要求，请选出并在答题卡上将该项涂黑）
1．下列属于一元二次方程的是（ ）
A．x2﹣3x+y＝0B．x
C．x2+5x＝0D．x（x2﹣4x）＝3
【分析】根据一元二次方程的定义逐个判断即可．
解：A．方程是二元二次方程，不是一元二次方程，故本选项不符合题意；
B．方程是分式方程，不是整式方程，不是一元二次方程，故本选项不符合题意；
C．方程是一元二次方程，故本选项符合题意；
D．方程是一元三次方程，不是一元二次方程，故本选项不符合题意；
故选：C．
【点评】本题考查了一元二次方程的定义，能熟记一元二次方程的定义是解此题的关键，只含有一个未知数，并且所含未知数的项的最高次数是2的整式方程叫一元二次方程．
2．随着贵州“村超”的火爆出圈，黔东南州榕江县搭乘“村超”快车，“超级星期六足球之夜”品牌价值日益彰显，旅游业持续升温．据初步测算，榕江县已累计接待游客50万人次，实现旅游综合收入12.41亿元这个数据用科学记数法表示为（ ）
A．12.41×108元B．1.241×109元
C．1.241×1010元D．1.241×108元
【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n是正数；当原数的绝对值＜1时，n是负数．
解：12.41亿元＝1241000000元＝1.241×109元．
故选：B．
【点评】此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．
3．把一元二次方程（x﹣1）2＝3x﹣2化为一般形式，若二次项系数是1，则一次项系数和常数项分别为（ ）
A．﹣3 和3B．﹣3 和1C．﹣5 和3D．﹣5 和1
【分析】先把方程化为一般式得到x2﹣5x+3＝0，然后根据一次项系数和常数项的定义求解．
解：去括号得x2﹣2x+1＝3x﹣2，
移项、合并得x2﹣5x+3＝0，
所以一次项系数为﹣5，常数项为3．
故选：C．
【点评】本题考查了一元二次方程的一般式：要确定二次项系数，一次项系数和常数项，必须先把一元二次方程化成一般形式．
4．用配方法解一元二次方程x2﹣4x﹣2＝0的过程中，配方正确的是（ ）
A．（x+2）2＝2B．（x﹣2）2＝2C．（x+2）2＝6D．（x﹣2）2＝6
【分析】利用解一元二次方程﹣配方法，进行计算即可解答．
解：x2﹣4x﹣2＝0，
x2﹣4x＝2，
x2﹣4x+4＝2+4，
（x﹣2）2＝6，
故选：D．
【点评】本题考查了解一元二次方程﹣配方法，熟练掌握解一元二次方程﹣配方法是解题的关键．
5．如果a是一元二次方程2x2＝6x﹣4的根，则代数式a2﹣3a+2024的值为（ ）
A．2021B．2022C．2023D．2024
【分析】根据一元二次方程的解的意义可得2a2＝6a﹣4，从而可得a2﹣3a＝﹣2，然后代入式子中进行计算，即可解答．
解：∵a是一元二次方程2x2＝6x﹣4的根，
∴2a2＝6a﹣4，
∴2a2﹣6a＝﹣4，
∴a2﹣3a＝﹣2，
∴a2﹣3a+2024＝﹣2+2024＝2022，
故选：B．
【点评】本题考查了一元二次方程的解，准确熟练地进行计算是解题的关键．
6．若方程ax2+bx+c＝0（a≠0），a、b、c满足a+b+c＝0和a﹣b+c＝0，则方程的根是（ ）
A．1，0B．﹣1，0C．1，﹣1D．无法确定
【分析】本题根据一元二次方程的根的定义、一元二次方程的定义求解，代入方程的左右两边，看左右两边是否相等．
解：在这个式子中，如果把x＝1代入方程，左边就变成a+b+c，又由已知a+b+c＝0可知：当x＝1时，方程的左右两边相等，即方程必有一根是1，同理可以判断方程必有一根是﹣1．则方程的根是1，﹣1．
故选：C．
【点评】本题就是考查了方程的解的定义，判断一个数是否是方程的解的方法，就是代入方程的左右两边，看左右两边是否相等．
7．如图，一块长16m，宽8m的矩形菜地，现要在中间铺设同样宽度的石子路，余下的部分用于种植，且种植面积为105m2．设石子路的宽度为xm，则下面所列方程正确的是（ ）
A．（16﹣x）（8﹣x）+x2＝105
B．（16﹣x）（8﹣x）＝105
C．（16﹣2x）（8﹣x）+x2＝105
D．（16﹣2x）（8﹣x）＝105
【分析】设小路的宽为xm，则草坪的总长度为（16﹣x）m，总宽度为（8﹣x）m，根据题意列出方程即可求出答案．
解：设小路的宽为xm，则草坪的总长度为（16﹣x）m，总宽度为（8﹣x）m，
根据题意，得：（16﹣x）（8﹣x）＝105．
故选：B．
【点评】本题考查了一元二次方程的应用，弄清楚草坪的总长度和总宽度是解题关键．
8．函数y＝自变量x的取值范围是（ ）
A．x≥﹣1B．x≠2C．x≥﹣1且x≠2D．﹣1≤x＜2
【分析】根据二次根式有意义的条件、分式有意义的条件列出不等式，解不等式得到答案．
解：由题意得，x+1≥0，x﹣2≠0，
解得，x≥﹣1且x≠2，
故选：C．
【点评】本题考查的是函数自变量的取值范围的确定，掌握二次根式的被开方数是非负数、分式的分母不为0是解题的关键．
9．若关于x的一元二次方程kx2+2x﹣1＝0有实数根，则k的取值范围是（ ）
A．k≥﹣1且k≠0B．k≥﹣1C．k＞﹣1D．k＞﹣1且k≠0
【分析】根据一元二次方程的定义和判别式的意义得到k≠0且Δ＝22﹣4k×（﹣1）≥0，然后求出两个不等式的公共部分即可．
解：根据题意得k≠0且Δ＝22﹣4k×（﹣1）≥0，
解得k≥﹣1且k≠0．
故选：A．
【点评】本题考查了一元二次方程ax2+bx+c＝0（a≠0）的根的判别式Δ＝b2﹣4ac：当Δ＞0，方程有两个不相等的实数根；当Δ＝0，方程有两个相等的实数根；当Δ＜0，方程没有实数根．也考查了一元二次方程的定义．
10．新冠肺炎奥密克戎变异株BA.5自2021年底出现后，目前已成为全球流行的变异株，更是近期深圳感染的主要毒株，潜伏期更短，传播力更强，传播速度更快．变异株2分钟左右进入宿主细胞，20﹣30分钟左右呈现指数复制，12﹣24小时后释放成熟的病毒颗粒，通过气溶胶等方式进行传播．若有两个人患了该新冠肺炎，经过两轮传播后共有338个人被传染，那么每轮传染中平均一个人传染几个人（ ）
A．13B．11C．12D．14
【分析】根据题意可得第一轮人数加第二轮人数，再加第三轮人数总数为338人，设平均每人感染x人，则列式为2（x+1）2＝338．即可解答．
解：设每轮传染中平均一个人传染了x个人，
根据题意，得2（x+1）2＝338．
解得：x＝12或x＝﹣14（舍去）．
∴每轮传染中平均一个人传染了12个人，
故选：C．
【点评】本题考查了一元二次方程的应用，找准等量关系，正确列出一元二次方程是解题的关键．
11．等腰三角形一边长为2，它的另外两条边的长度是关于x的一元二次方程x2﹣6x+k＝0的两个实数根，则k的值是（ ）
A．8B．9C．8或9D．12
【分析】根据一元二次方程的解法以及等腰三角形的性质即可求出答案．
解：当等腰三角形的底边为2时，
此时关于x的一元二次方程x2﹣6x+k＝0的有两个相等实数根，
∴Δ＝36﹣4k＝0，
∴k＝9，
此时两腰长为3，
∵2+3＞3，
∴k＝9满足题意，
当等腰三角形的腰长为2时，
此时x＝2是方程x2﹣6x+k＝0的其中一根，
∴4﹣12+k＝0，
∴k＝8，
此时另外一根为：x＝4，
∵2+2＝4，
∴不能组成三角形，
综上所述，k＝9，
故选：B．
【点评】本题考查一元二次方程，解题的关键是熟练运用一元二次方程的解法以及等腰三角形的性质，本题属于中等题型．
12．如图1，矩形ABCD中，点E为BC的中点，点P沿BC从点B运动到点C，设B，P两点间的距离为x，PA﹣PE＝y，图2是点P运动时y随x变化的关系图象，则BC的长为（ ）
A．6B．7C．8D．9
【分析】当x＝0，即P在B点时，BA﹣BE＝1；利用两点之间线段最短，得到PA﹣PE≤AE，得y的最大值为AE＝5；在Rt△ABE中，由勾股定理求出BE的长，再根据BC＝2BE求出BC的长．
解：由函数图象知：当x＝0，即P在B点时，BA﹣BE＝1．
利用两点之间线段最短，得到PA﹣PE≤AE．
∴y的最大值为AE，
∴AE＝5．
在Rt△ABE中，由勾股定理得：BA2+BE2＝AE2＝25，
设BE的长度为t，
则AB＝t+1，
∴（t+1）2+t2＝25，
即t2+t﹣12＝0，
∴（t﹣3）（t+4）＝0，
解得t＝3或t＝﹣4，
由于t＞0，
∴t＝3．
∴BE＝3，
∵点E为BC的中点，
∴BC＝6．
故选：A．
【点评】本题考查了动点问题的函数图象，根据勾股定理求出BE的长是解题的关键．
二、填空题（本题共4小题，每小题4分，共16分）
13．方程（x+2）2＝8，则方程的根为 x＝2﹣2或x＝﹣2﹣2 ．
【分析】利用直接开平方法解方程即可．
解：（x+2）2＝8，
x+2＝2或x+2＝﹣2，
x＝2﹣2或x＝﹣2﹣2，
故答案为：x＝2﹣2或x＝﹣2﹣2．
【点评】本题考查解一元二次方程，熟练掌握开平方法解一元二次方程的方法是解题的关键．
14．若方程是关于x的一元二次方程，则a的值为 4 ．
【分析】利用一元二次方程的定义判断即可求出a的值．
解：∵方程是关于x的一元二次方程，
∴a2﹣14＝2且a+4≠0，
解得：a＝4．
故答案为：4．
【点评】此题考查了一元二次方程的定义，熟练掌握一元二次方程的定义是解本题的关键．
15．一个两位数，十位上的数字比个位上的数字的平方少9．如果把十位上的数字与个位上的数字对调，得到的两位数比原来的两位数小27，则原来的两位数是 74 ．
【分析】等量关系为：原来的两位数﹣新两位数＝27，把相关数值代入计算可得各位上的数字，根据两位数的表示方法求得两位数即可．
解：设原两位数个位上的数字为x，则十位上的数字为（x2﹣9）．
∴10（x2﹣9）+x﹣10x﹣（x2﹣9）＝27，
解得x1＝4，x2＝﹣3（不符合题意，舍去）．
∴x2﹣9＝7，
∴10（x2﹣9）+x＝74．
答：原两位数为74．
故答案为：74．
【点评】此题主要考查了一元二次方程的应用；得到两个两位数之间的等量关系是解决本题的关键；用到的知识点为：两位数＝10×十位数字+个位数字．
16．已知：m2﹣2m﹣1＝0，n2+2n﹣1＝0且mn≠1，则的值为 3 ．
【分析】将n2+2n﹣1＝0变形为_﹣1＝0，据此可得m，是方程x2﹣2x﹣1＝0的两根，由韦达定理可得m+＝2，代入＝m+1+可得．
解：由n2+2n﹣1＝0可知n≠0．
∴1+﹣＝0．
∴﹣﹣1＝0，
又m2﹣2m﹣1＝0，且mn≠1，即m≠．
∴m，是方程x2﹣2x﹣1＝0的两根．
∴m+＝2．
∴＝m+1+＝2+1＝3，
故答案为：3．
【点评】本题主要考查根与系数的关系，解题的关键是将方程变形后得出m，是方程x2﹣2x﹣1＝0的两根及韦达定理．
三、解答题（本题共9小题，共98分）
17．计算题：
（1）；
（2）解方程：（3﹣y）2+y2＝12．
【分析】（1）原式利用绝对值的代数意义，负整数指数幂，零指数幂，以及二次根式的运算法则计算即可；
（2）方程整理后，利用公式法求出解即可．
解：（1）原式＝﹣8+2﹣+3﹣2﹣1
＝﹣6﹣；
（2）方程整理得：2y2﹣6y﹣3＝0，
这里a＝2，b＝﹣6，c＝﹣3，
∵Δ＝36+24＝60＞0，
∴x＝＝，
解得：x1＝，x2＝．
【点评】此题考查了解一元二次方程﹣公式法，实数的运算，零指数幂，以及二次根式的运算，熟练掌握运算法则及方程的解法是解本题的关键．
18．先化简，再求值：÷（m+3+），其中m是方程x2﹣2x﹣1＝0的根．
【分析】根据分式的混合运算法则把原式化简，利用因式分解法解出方程，根据分式有意义的条件得到m的值，把m的值代入计算，得到答案．
解：÷（m+3+）
＝÷
＝•
＝．
解方程x2﹣2x﹣1＝0得，x1＝+1，x2＝﹣+1，
所以m（m﹣2）＝（+1）（+1﹣2）＝（+1）（﹣1）＝1．
或m（m﹣2）＝（﹣+1）（﹣+1﹣2）＝（+1）（﹣1）＝1．
所以原式＝．
【点评】本题考查的是分式的化简求值、一元二次方程的解法，掌握分式的混合运算法则、因式分解法解一元二次方程的一般步骤是解题的关键．
19．如图，在平面直角坐标系中，A（﹣4，1），B（﹣3，3），C（﹣1，2）是△ABC的顶点．
（1）画出△ABC关于y轴的对称图形△A1B1C1；
（2）直接写出点C1的坐标；
（3）在y轴上找一点P使PA+PC最小，求出P点坐标为 （0，） ．
【分析】（1）根据轴对称的性质作图即可．
（2）由图可得答案．
（3）连接AC1，交y轴于点P，此时PA+PC最小，即可得出答案．
解：（1）如图，△A1B1C1即为所求．
（2）由图可得，点C1的坐标为（1，2）．
（3）连接AC1，交y轴于点P，此时PA+PC最小，
设点P坐标为（0，m），
则，
解得m＝，
∴P点坐标为（0，）．
故答案为：（0，）．
【点评】本题考查作图﹣轴对称变换、轴对称﹣最短路线问题，熟练掌握轴对称的性质是解答本题的关键．
20．已知方程x2﹣4x+m＝0的一个根为﹣2，求方程的另一根及m的值．
【分析】把x＝﹣2代入方程x2﹣4x+m＝0得出4+8+m＝0，求出m，得出方程x2﹣4x﹣12＝0，设方程的另一个根为a，则a+（﹣2）＝4，求出a即可．
解：把x＝﹣2代入方程x2﹣4x+m＝0得：4+8+m＝0，
解得：m＝﹣12，
即方程为x2﹣4x﹣12＝0，
设方程的另一个根为a，则a+（﹣2）＝4，
即得：a＝6，
即方程的另一根为6，m＝﹣12．
【点评】本题考查了根与系数的关系和一元二方程的解，能熟记根与系数的关系的内容是解此题的关键，已知一元二次方程ax2+bx+c＝0（a、b、c为常数，a≠0）的两个根为x1和x2，则x1+x2＝﹣，x1•x2＝．
21．如图所示，在Rt△ABC中，∠B＝90°，AB＝6cm，BC＝12cm，点P从点B开始沿边BA以1cm/s的速度向点A移动，同时点Q也从点B开始沿BC边以2cm/s的速度向点C移动，当其中一点到达A或者C时停止运动．
（1）几秒后PQ长度为6cm？
（2）几秒后△PBQ的面积是24平方厘米？
【分析】设t秒后△PBQ的面积等于24平方厘米，分别表示出线段PB和线段BQ的长，然后根据△PBQ的面积为24平方厘米列出方程求得时间即可．
解：（1）设x秒后PQ长度为6cm，
PQ＝
解得：t1＝﹣（不合题意舍去），t2＝．
答：秒后PQ长度为6cm，
（2）设t秒后△PBQ的面积等于24平方厘米，根据题意得：
×2t×t＝24，
解得：t1＝﹣2（不合题意舍去），t2＝2．
答：2秒后△PBQ的面积等于24平方厘米．
【点评】本题考查了一元二次方程的应用，能够表示出线段PB和QB的长是解答本题的关键．
22．已知关于x的一元二次方程x2+（2k+1）x+k2+k＝0（k为常数）．
（1）求证：无论k取何值，方程都有两个不相等的实数根；
（2）若方程的两个实数根x1，x2满足x1+x2＝x1•x2﹣1，求k的值．
【分析】（1）根据根的判别式得出Δ，据此可得答案；
（2）根据根与系数的关系得出x1+x2＝﹣（2k+1），x1x2＝k2+k，代入x1+x2＝x1x2﹣1得出关于k的方程，解之可得答案．
【解答】（1）证明：∵Δ＝（2k+1）2﹣4×1×（k2+k）
＝4k2+4k+1﹣4k2﹣4k
＝1＞0，
∴无论k取何值，方程都有两个不相等的实数根；
（2）解：由根与系数的关系得出：x1+x2＝﹣（2k+1），x1x2＝k2+k，
由x1+x2＝x1•x2﹣1，得：﹣（2k+1）＝k2+k﹣1，
解得：k＝0或﹣3，
∴k的值为0或﹣3．
【点评】本题主要考查根与系数的关系、根的判别式，解题的关键是掌握x1，x2是方程x2+px+q＝0的两根时，x1+x2＝﹣p，x1x2＝q．
23．某扶贫单位为了提高贫困户的经济收入，购买了39m的铁栅栏，准备用这些铁栅栏为贫困户靠墙（墙长15m）围建一个中间带有铁栅栏的矩形养鸡场（如图所示）．
（1）若要建的矩形养鸡场面积为120m2，求鸡场的长AB和宽BC；
（2）该扶贫单位想要建一个130m2的矩形养鸡场，这一想法能实现吗？请说明理由．
【分析】（1）设BC＝xm，则可表示出长AB，由面积关系即可列出方程，解方程即可．
（2）设BC＝xm，则可表示出长AB，由面积关系即可列出方程，根据方程是否有解或方程的解是否符合题意，即可作出判断．
解：（1）设BC＝xm，则AB＝（39﹣3x）m，
由题意得：x（39﹣3x）＝120，
整理得：x2﹣13x+40＝0，
解得：x1＝5，x2＝8，
当x＝5时，39﹣3x＝24＞15，不符合题意；当x＝8时，39﹣3x＝15，符合题意；
答：鸡场的长AB和宽BC分别为15m与8m．
（2）设BC＝xm，则AB＝（39﹣3x）m，
由题意得：x（39﹣3x）＝130，
整理得：3x2﹣39x+130＝0，
Δ＝（﹣39）2﹣4×3×130＝1521﹣1560＜0，
方程无实数解；
所以想法不能实现．
【点评】本题考查了一元二次方程的应用，正确列出方程是解题的关键．
24．“小龙虾”是我县特色农业的拳头产品，在南县被广泛养殖．2020年估计某村养殖面积有100亩，到2022年该村养殖面积达到196亩．
（1）求该村这两年“小龙虾”养殖面积的平均增长率；
（2）某养殖户调查发现，当“小龙虾”的售价为20元/千克时，每天能售出200千克，售价每降价1元，每天可多售出50千克．为了推广宣传，该养殖户决定降价促销，同时减少存量，已知“小龙虾”的平均成本为12元/千克，若要确保每天获利1750元，则售价应该降低多少元？
【分析】（1）设平均增长率为x，则根据a（1+x）n＝b，即可列出方程．其中，a＝100，n＝2，b＝196；
（2）设售价降低m元，则每天的数量为（200+50m）千克，根据总利润＝单利×数量，即可列出方程，因为减少存量，则取较大的解即可．
解：（1）设平均增长率为x，
100（1+x）2＝196，
1+x＝±1.4，
x1＝﹣2.4（舍），x2＝0.4，
答：平均增长率为40%．
（2）设售价降低m元，
（20﹣12﹣m）（200+50m）＝1750，
m2﹣4m+3＝0，
m1＝1，m2＝3，
∵减少存量，
∴m＝3．
答：降3元可获利1750元，同时减少了存量．
【点评】本题考查一元二次方程的应用，找准等量关系，正确列出方程是关键；本题还需要注意数量的表示．
25．如图①，在△ABC中，AD⊥BC于D，BC＝14，AD＝8，BD＝6，点E是AD上一动点（不与点A，D重合），在△ADC内作矩形EFGH，点F在DC上，点G、H在AC上，设DE＝x，连接BE．
（1）设矩形EFGH的面积为S1，△ABE的面积为S2，令y＝，求y关于x的函数解析式；（要求写出自变量的取值范围）
（2）如图②，点M是（1）中得到的函数图象上的任意一点，N的坐标为（2，0），当△OMN为等腰三角形时，求点M的坐标．
​
【分析】（1）由题意可求出CD＝8＝AD，即得出∠DAC＝∠DCA＝45°，再结合矩形的性质可求出∠DFE＝∠DEF＝∠DAC＝∠DCA＝45°，即得出DE＝DF＝x，从而得出AE＝CF＝8﹣x，，进而可求出S2＝．又可证AH＝EH，结合勾股定理可求出，从而可求出S1＝EF•EH＝8x﹣x2，再作比，化简即可得出答案，最后由题意即可确定x的取值范围；
（2）根据题意画出图象，分类讨论：①当OM＝MN时，如图点M1；②当OM＝ON时，如图点M2；③当MN＝ON时，如图点M3，分别根据等腰三角形的定义结合勾股定理即可求解．
解：（1）∵BC＝14，AD＝8，BD＝6，
∴CD＝8＝AD．
∵AD⊥BC，
∴∠DAC＝∠DCA＝45°．
∵四边形EFGH是矩形，
∴EF∥AC，∠AHE＝∠CGF＝90°．
∴∠DFE＝∠DEF＝∠DAC＝∠DCA＝45°，
∴DE＝DF＝x，
∴AE＝CF＝8﹣x，，
∴S2＝S△ABE＝，
∵∠DAC＝45°，∠AHE＝90°，
∴AH＝EH．
∵AH2+EH2＝AE2，
，
∴S1＝S矩形EFGH＝EF•EH＝，
∴，
∵点E是AD上一动点（不与点A，D重合），
∴0＜x＜8，
∴y关于x的函数解析式为．
（2）分类讨论：①当OM＝MN时，如图点M1，
∵N（2.0），
∴＝1，
∴＝，
∴此时M点坐标为；
②当OM＝ON时，如图点M2，过点M2作M2P⊥x轴于点P，
∵N（2，0），
∴OM2＝ON＝2，
设，
∴，
解得（舍去负值），
∴，
∴此时M点坐标为；
③当MN＝ON时，如图点M3，过点M3作M3Q⊥x轴于点Q，
∵N（2，0），
∴M3N＝ON＝2，
设，
∴NQ＝b﹣2，
∵，
∴，
解得，b2＝0（舍），
∴．
∴此时M点坐标为．
综上，点M的坐标为或或．
【点评】本题考查几何变换的综合应用，主要考查矩形的性质，一次函数的实际应用，等腰三角形的定义，等腰直角三角形的判定和性质，勾股定理，一元二次方程的实际应用等知识．利用数形结合和分类讨论的思想是解题关键．