备战2024年高考第一轮专题复习专题25 异面直线所成角【艺体生专供—选择填空抢分专题】备战2024年高考高频考点题型精讲+精练（新高考通用）原卷版

这是一份备战2024年高考第一轮专题复习专题25 异面直线所成角【艺体生专供—选择填空抢分专题】备战2024年高考高频考点题型精讲+精练（新高考通用）原卷版，共28页。试卷主要包含了考向解读，知识点汇总，题型专项训练，高考真题及模拟题精选，题型精练，巩固基础等内容，欢迎下载使用。
一、考向解读
考向：高考中主要以选择填空题的类型考查，属于立体几何中较为容易拿分的点，学会使用解三角形的相关结论和向量法是解题关键!
考点：异面直线所成角
导师建议：没有思路的时候考虑向量法，虽然计算量大一点，但是稳妥！
二、知识点汇总
1.异面直线所成角范围：
2.求异面直线所成的角的步骤
一作，即依据定义作平行线,作出异面直线所成的角
二证，即证明作出的角是异面直线所成的角
三求，解三角形,求出作出的角,如果求出的角是锐角或直角,则它就是要求的角,如果求出的角是钝角,则它的补角才是要求的角
3.向量法
已知为两异面直线，A，C与B，D分别是上的任意两点，所成的角为，则
三、题型专项训练
目录一览
①直接平移后相交
一、单选题
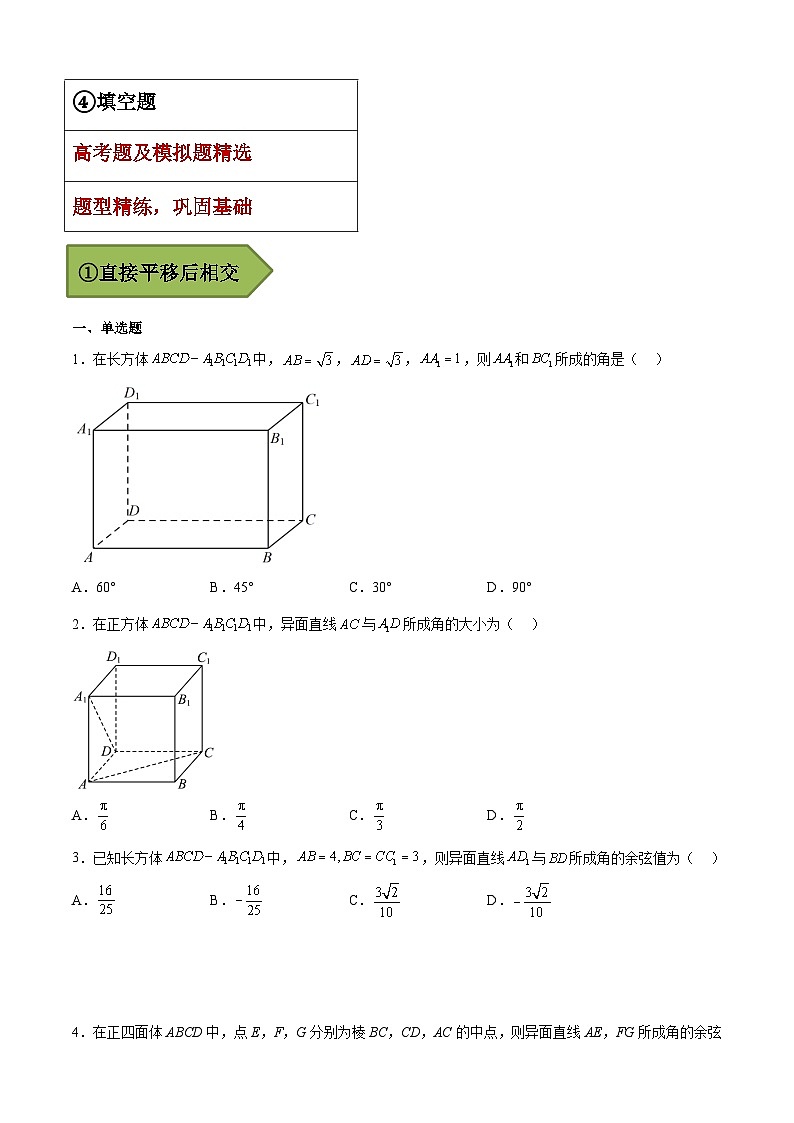
1．在长方体中，，，，则和所成的角是（ ）
A．60°B．45°C．30°D．90°
2．在正方体中，异面直线与所成角的大小为（ ）
A．B．C．D．
3．已知长方体中，，则异面直线与所成角的余弦值为（ ）
A．B．C．D．
4．在正四面体ABCD中，点E，F，G分别为棱BC，CD，AC的中点，则异面直线AE，FG所成角的余弦值为（ ）
A．B．C．D．
5．已知三棱锥中，平面，，，，则异面直线与所成角的余弦值为（ ）
A．B．C．D．
6．如图，已知等腰直角三角形的斜边的中点为，且，点为平面外一点，且，，则异面直线与所成的角的余弦值为（ ）
A．B．C．D．
②利用中位线平移
7．在正方体中,分别为的中点,则异面直线与所成角的大小为（ ）
A．B．C．D．
8．如图，在长方体中，已知，，E为的中点，则异面直线BD与CE所成角的余弦值为（ ）
A．B．C．D．
9．在正方体中，是的中点，则异面直线与所成角的余弦值为（ ）
A．B．C．D．
10．如图所示，在正方体中，E，F分别是AB，AD的中点，则异面直线与所成的角的大小为（ ）
A．90°B．60°C．45°D．30°
11．在正四面体中，分别为的中点，则异面直线所成角的余弦值为（ ）
A．B．C．D．
12．如图，在正三棱柱中，，，则异面直线与所成角的余弦值为（ ）
A．B．C．D．
13．已知直三棱桂：的底面为等腰直角三角形，分别为，的中点，为上一点，，则异面直线与所成角的余弦值为（ ）
A．B．C．D．
14．在正四棱锥P-ABCD中，，E为PC的中点，则异面直线AP与DE所成角的余弦值为（ ）
A．B．C．D．
③向量法
15．如图所示，在几何体ABCDEF中，，，，，，平面ABCD，则异面直线EF与AB所成的角为（ ）
A．B．C．D．
16．长方体中，为的中点，则异面直线与所成的角的余弦值为（ ）
A．B．C．D．
17．在直三棱柱中，分别是的中点，，则与所成角的正弦值是（ ）
A．B．C．D．
18．如图，在正方体中，棱长为为的中点，则直线与直线所成角的余弦值为（ ）
A．B．C．D．
19．如图，在三棱锥M－EFG中，，EF=FG=2，平面平面EFG，则异面直线ME与FG所成角的余弦值为（ ）
A．B．C．D．
20．如图，在三棱锥中，平面，，，，分别为的中点，则异面直线所成角的余弦值为（ ）
B．C．D．
④填空题
二、填空题
21．如图,在正方体中,点E,F分别是棱AD,的中点,则异面直线与BF所成角的大小为______．
22．如图，在直三棱柱中，D为的中点，，，则异面直线BD与AC所成的角为________．
23．如图，平面，且，则异面直线与所成角的大小是__．
24．设、分别在正方体的棱、上，且，，则直线与所成角的余弦值为_____________．
25．如图，在直三棱柱ABC—A1B1C1中，，，，D、E分别是、的中点，则异面直线与所成的角的余弦值为_________.
三棱锥中，两两垂直，，点M为平面内的动点，且满足，记直线与直线的所成角的余弦值的取值范围为_____________．
四、高考真题及模拟题精选
一、单选题
1．（2023·陕西商洛·统考一模）如图，在长方体中，已知，，E为的中点，则异面直线BD与CE所成角的余弦值为（ ）
A．B．C．D．
2．（2021·全国·统考高考真题）在正方体中，P为的中点，则直线与所成的角为（ ）
A．B．C．D．
3．（2023·陕西安康·统考二模）已知四面体的四个面均为直角三角形（如图所示），则该四面体中异面直线AB与CD所成角的余弦值为（ ）
A．B．C．D．
4．（2023·安徽·统考一模）安徽徽州古城与四川阆中古城､山西平遥古城､云南丽江古城被称为中国四大古城.徽州古城中有一古建筑，其底层部分可近似看作一个正方体.已知该正方体中，点分别是棱的中点，过三点的平面与平面的交线为，则直线与直线所成角为（ ）
A．B．C．D．
5．（2023·河南·统考模拟预测）如图，在正方体中，M，N分别为AC，的中点，则下列说法中不正确的是（ ）
A．平面
B．
C．直线MN与平面ABCD所成的角为60°
D．异面直线MN与所成的角为45°
6．（2023·陕西榆林·统考二模）如图，在正三棱柱中，，是棱的中点，在棱上，且，则异面直线与所成角的余弦值是（ ）
A．B．C．D．
7．（2023·全国·模拟预测）如图，在三棱锥M－EFG中，，EF=FG=2，平面平面EFG，则异面直线ME与FG所成角的余弦值为（ ）
A．B．C．D．
8．（2022·浙江·统考高考真题）如图，已知正三棱柱，E，F分别是棱上的点．记与所成的角为，与平面所成的角为，二面角的平面角为，则（ ）
A．B．C．D．
二、填空题
9．（2022·全国·校联考模拟预测）已知直三棱柱中，，，，则异面直线与所成角的余弦值为______．
10．（2022·吉林长春·统考模拟预测）四面体的各棱长均相等，E，F分别为AD，BC的中点，则异面直线AB与EF所成角的大小为______．
11．（2023·河北邯郸·统考一模）在正四棱锥P－ABCD中，，点E，F满足，，则异面直线BE与CF所成角的余弦值为_______________．
12．（2022·浙江宁波·统考一模）在棱长均相等的四面体ABCD中，P为棱AD（不含端点）上的动点，过点A的平面α与平面PBC平行．若平面α与平面ABD，平面ACD的交线分别为m，n，则m，n所成角的正弦值的最大值为__________．
五、题型精练，巩固基础
一、单选题
1．（2023·青海西宁·统考一模）如图，在正三棱柱中，为的中点，则与所成角的余弦值为（ ）
A．B．C．D．
2．（2023·湖南株洲·统考一模）已知三棱锥的侧面展开图放在正方形网格中的位置如图所示，那么在三棱锥中，与所成的角为（ ）
A．B．C．D．
3．（2023·河南焦作·统考模拟预测）在直三棱柱中，，且，若直线与侧面所成的角为，则异面直线与所成的角的正弦值为（ ）
A．B．C．D．
4．（2023·内蒙古·校联考模拟预测）在直三棱柱中，是等边三角形，，D，E，F分别是棱，，的中点，则异面直线BE与DF所成角的余弦值是（ ）
A．B．C．D．
5．（2023·广西梧州·统考一模）在正方体中，E，F分别是线段，的中点，则异面直线，EF所成角余弦值是（ ）
A．B．C．D．
6．（2023·山西忻州·统考模拟预测）如图，在四棱锥中，平面平面，四边形是矩形，，分别是棱 的中点，则异面直线与所成角的余弦值是（ ）
A．B．C．D．
7．（2023·河南·校联考模拟预测）如图，已知正三棱柱的棱长都相等，为棱的中点，则与所成角的正弦值为（ ）
A．B．C．D．
8．（2023·黑龙江大庆·统考一模）在三棱锥中，平面ABC，且，，E，F分别为BC，PA的中点，则异面直线EF与PC所成角的余弦值为（ ）
A．B．C．D．
9．（2023·贵州毕节·统考一模）图（1）是由正方形和正三角形组合而成的平面图形，将三角形沿折起，使得平面平面，如图（2），则异面直线与所成角的大小为（ ）
A．B．C．D．
10．（2023·全国·模拟预测）如图，在正方体中，点P在线段上运动（包含端点），则直线与所成角的取值范围是（ ）
A．B．
C．D．
11．（2023·全国·模拟预测）如图，已知正四棱锥的底面边长和高分别为2和1，若点E是棱PD的中点，则异面直线PA与CE所成角的余弦值为（ ）
A．B．C．D．
12．（2022·河南安阳·校联考模拟预测）如图，在四面体ABCD中，平面BCD，，P为AC的中点，则直线BP与AD所成的角为（ ）
A．B．C．D．
13．（2023·陕西西安·西北工业大学附属中学校考二模）如图，在三棱锥中，平面，，，侧棱与平面所成的角为，为的中点，是侧棱上一动点，当的面积最小时，异面直线与所成角的余弦值为（ ）
A．B．C．D．
14．（2023·河南南阳·统考二模）如图，已知正三棱柱的各条棱长都相等，是侧棱的中点，是的中点，则（ ）
A．B．平面
C．平面D．
15．（2023·陕西渭南·统考一模）如图，在直三棱柱中，，且分别是棱的中点，则异面直线与所成角的余弦值是（ ）
A．B．C．D．
16．（2023·四川·校联考一模）在长方体中，已知异面直线与，与AB所成角的大小分别为和，则直线和平面所成的角的余弦值为（ ）
A．B．C．D．
二、填空题
17．（2022·黑龙江牡丹江·牡丹江市第三高级中学校考三模）在长方体ABCD－A1B1C1D1中，AB＝3，AD＝4，AA1＝2，则异面直线AC和BC1所成角的余弦值是_________.
18．（2022·陕西商洛·统考二模）在正方体中，点P是底面的中心，则直线与所成角的余弦值为___________.
19．（2022·河南开封·通许县第一高级中学校联考模拟预测）已知三棱柱的底面是边长为2的等边三角形，为的中点，若，则侧面四边形为正方形，则异面直线与所成角的余弦值为___________.
20．（2022·河南·统考模拟预测）在平行四边形中，，，现将平行四边形沿对角线折起，当异面直线和所成的角为时，的长为__________.
21．（2022·河南·校联考模拟预测）已知在三棱锥S-ABC中，SA⊥底面ABC，AB⊥BC，SA＝AB＝BC，则异面直线SC与AB所成角的余弦值为______．
22．（2022·吉林长春·统考模拟预测）现有四棱锥（如图），底面ABCD是矩形，平面ABCD.，，点E，F分别在棱AB，BC上.当空间四边形PEFD的周长最小时，异面直线PE与DF所成角的余弦值为___________.
23．（2022·重庆·重庆八中校考模拟预测）如图所示，是棱长为的正方体，、分别是下底面的棱、的中点，是上底面的棱上的一点，，过、、的平面交上底面于，在上，则异面直线与所成角的余弦值为___________．
24．（2022·青海·统考模拟预测）手工课可以提高学生的动手能力、反应能力、创造力，使学生在德、智、体、美、劳各方面得到全面发展，某小学生在一次手工课上制作了一座漂亮的房子模型，它可近似地看成是一个直三棱柱和一个长方体的组合图形，其直观图如图所示，，，P，Q，M，N分别是棱AB，，，的中点，则异面直线PQ与MN所成角的余弦值是______．
①直接平移后相交
②利用中位线平移
③向量法
④填空题
高考题及模拟题精选
题型精练，巩固基础