人教A版 (2019)必修 第一册5.4 三角函数的图象与性质习题

这是一份人教A版 (2019)必修 第一册5.4 三角函数的图象与性质习题，共9页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

A 组·基础自测
一、选择题
1．用“五点法”画函数y＝1＋eq \f(1,2)sin x的图象时，首先应描出五点的横坐标是( B )
A．0，eq \f(π,4)，eq \f(π,2)，eq \f(3π,4)，π B．0，eq \f(π,2)，π，eq \f(3π,2)，2π
C．0，π，2π，3π，4π D．0，eq \f(π,6)，eq \f(π,3)，eq \f(π,2)，eq \f(2π,3)
[解析] 利用五点法作图的要求可知，选B.
2．函数y＝1－sin x，x∈[0,2π]的大致图象是( B )
[解析] 利用代入特殊值法即可得出选B.
3．在[0,2π]上满足sin x≥eq \f(1,2)的x的取值范围是( B )
A．eq \b\lc\[\rc\](\a\vs4\al\c1(0，\f(π,6))) B．eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,6)，\f(5π,6)))
C．eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,6)，\f(2π,3))) D．eq \b\lc\[\rc\](\a\vs4\al\c1(\f(5π,6)，π))
[解析] 由函数y＝sin x，x∈[0,2π]的图象，可知eq \f(π,6)≤x≤eq \f(5π,6).
4．如图所示的曲线对应的函数解析式可以是下列选项中的( C )
A．y＝|sin x| B．y＝sin |x|
C．y＝－sin |x| D．y＝－|sin x|
[解析] 将eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)，－1))代入4个解析式，排除A，B；将eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3π,2)，1))代入C，D中的解析式，排除D，故选C.
5．函数y＝cs x＋|cs x|，x∈[0,2π]的大致图象为( D )
[解析] y＝cs x＋|cs x|
＝eq \b\lc\{\rc\ (\a\vs4\al\c1(2cs x，x∈\b\lc\[\rc\](\a\vs4\al\c1(0，\f(π,2)))∪\b\lc\[\rc\](\a\vs4\al\c1(\f(3π,2)，2π))，,0，x∈\b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)，\f(3π,2)))，))故选D.
二、填空题
6．已知函数f(x)＝3＋2cs x的图象经过点eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,3)，b))，则b＝_4_.
[解析] b＝feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,3)))＝3＋2cseq \f(π,3)＝4.
7．若方程sin x＝4m＋1在x∈[0,2π]上有解，则实数m的取值范围是 eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(1,2)，0))_.
[解析] 由正弦函数的图象，知当x∈[0,2π]时，sin x∈[－1,1]，要使得方程sin x＝4m＋1在x∈[0，2π]上有解，则－1≤4m＋1≤1，故－eq \f(1,2)≤m≤0.
8．函数y＝lg2(2sin x＋1)的定义域为 eq \b\lc\{\rc\}(\a\vs4\al\c1(x|－\f(π,6)＋2kπ[解析] 要使函数有意义，则必有2sin x＋1>0，即sin x>－eq \f(1,2).画出y＝sin x，x∈eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(π,2)，\f(3π,2)))的草图，如图所示．
当－eq \f(π,6)－eq \f(1,2)成立，所以sin x>－eq \f(1,2)的解集为eq \b\lc\{\rc\}(\a\vs4\al\c1(x|－\f(π,6)＋2kπ可知函数y＝lg2(2sin x＋1)的定义域为eq \b\lc\{\rc\}(\a\vs4\al\c1(x|－\f(π,6)＋2kπ三、解答题
9．利用“五点法”作出下列函数的简图．
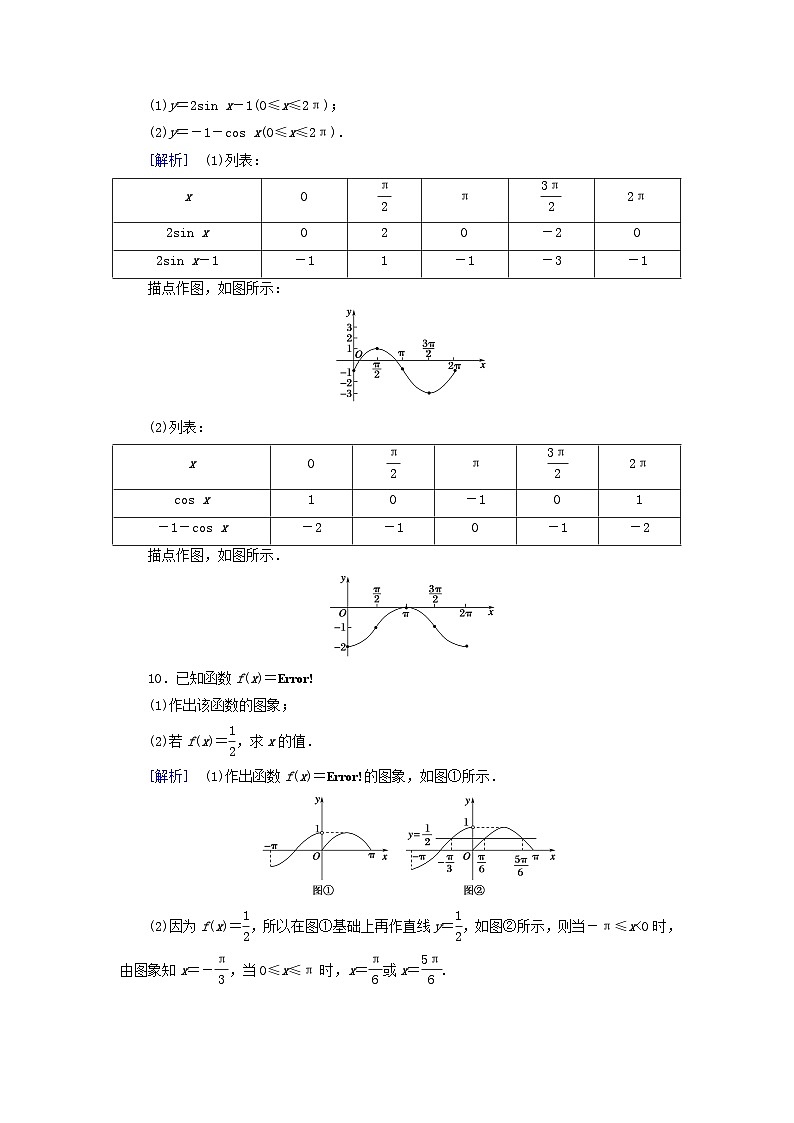
(1)y＝2sin x－1(0≤x≤2π)；
(2)y＝－1－cs x(0≤x≤2π)．
[解析] (1)列表：
描点作图，如图所示：
(2)列表：
描点作图，如图所示．
10．已知函数f(x)＝eq \b\lc\{\rc\ (\a\vs4\al\c1(cs x－π≤x<0，,sin x0≤x≤π.))
(1)作出该函数的图象；
(2)若f(x)＝eq \f(1,2)，求x的值．
[解析] (1)作出函数f(x)＝eq \b\lc\{\rc\ (\a\vs4\al\c1(cs x－π≤x<0，,sin x0≤x≤π))的图象，如图①所示．
(2)因为f(x)＝eq \f(1,2)，所以在图①基础上再作直线y＝eq \f(1,2)，如图②所示，则当－π≤x<0时，由图象知x＝－eq \f(π,3)，当0≤x≤π时，x＝eq \f(π,6)或x＝eq \f(5π,6).
综上，可知x的值为－eq \f(π,3)或eq \f(π,6)或eq \f(5π,6).
B 组·能力提升
一、选择题
1．已知f(x)＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,2)))，g(x)＝cseq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,2)))，则f(x)的图象( D )
A．与g(x)的图象相同
B．与g(x)的图象关于y轴对称
C．向左平移eq \f(π,2)个单位长度，得g(x)的图象
D．向右平移eq \f(π,2)个单位长度，得g(x)的图象
[解析] f(x)＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,2)))，g(x)＝cseq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,2)))＝cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)－x))＝sin x，
f(x)的图象向右平移eq \f(π,2)个单位长度得到g(x)的图象．故选D.
2．(多选题)下列在(0,2π)上的区间能使cs x>sin x成立的是( AC )
A．eq \b\lc\(\rc\)(\a\vs4\al\c1(0，\f(π,4))) B．eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,4)，\f(5π,4)))
C．eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(5π,4)，2π)) D．eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,4)，\f(π,2)))∪eq \b\lc\(\rc\)(\a\vs4\al\c1(π，\f(5π,4)))
[解析] 在同一平面直角坐标系中画出正、余弦函数的图象，在(0,2π)上，当cs x＝sin x时，x＝eq \f(π,4)或x＝eq \f(5π,4)，结合图象可知满足cs x>sin x的是eq \b\lc\(\rc\)(\a\vs4\al\c1(0，\f(π,4)))和eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(5π,4)，2π))，故选AC.
3．(多选题)若函数f(x)＝2cs x(0≤x≤2π)的图象和直线y＝2围成一个封闭的平面图形，则下列说法正确的是( AC )
A．当x∈eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)，\f(3π,2)))时，y<0
B．f(0)＝1
C．feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3π,2)))＝0
D．阴影部分的面积为2π
[解析] 作出函数y＝2cs x，x∈[0,2π]的图象，函数y＝2cs x，x∈[0,2π]的图象与直线y＝2围成的平面图形为如图所示的阴影部分，由图可知，A正确；B错误；C正确；
利用图象的对称性，可知该阴影部分的面积等于矩形OABC的面积，又∵OA＝2，OC＝2π，
∴S阴影部分＝S矩形OABC＝2×2π＝4π，∴D错误．故选AC.
二、填空题
4．已知函数f(x)＝－1＋eq \r(2)cs x的图象经过点eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,4)，,b))，则b＝_0_.
[解析] ∵函数f(x)＝－1＋eq \r(2)cs x的图象经过点eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,4)，b))，∴b＝feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,4)))＝－1＋eq \r(2)cseq \f(π,4)＝－1＋eq \r(2)×eq \f(\r(2),2)＝0.
5．方程sin x＝eq \f(x,10)的根的个数是_7_个．
[解析] 在同一坐标系内画出y＝eq \f(x,10)和y＝sin x的图象如图所示：
根据图象可知方程有7个根．
三、解答题
6．若方程sin x＝eq \f(1－a,2)在x∈eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,3)，π))上有两个实数根，求a的取值范围．
[解析] 首先作出y＝sin x，x∈eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,3)，π))的图象，然后再作出y＝eq \f(1－a,2)的图象，如果y＝sin x，x∈eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,3)，π))与y＝eq \f(1－a,2)的图象有两个交点，方程sin x＝eq \f(1－a,2)，x∈eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,3)，π))就有两个实数根．设y1＝sin x，x∈eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,3)，π))，y2＝eq \f(1－a,2).y1＝sin x，x∈eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,3)，π))的图象如图．
由图象可知，当eq \f(\r(3),2)≤eq \f(1－a,2)<1，即－1C 组·创新拓展
已知函数f(x)＝cs x＋2|cs x|，x∈[0,2π]，若直线y＝k与函数y＝f(x)的图象有四个不同的交点，则实数k的取值范围是_(0,1)_.
[解析] 函数f(x)＝cs x＋2|cs x|＝eq \b\lc\{\rc\ (\a\vs4\al\c1(3cs x，x∈\b\lc\[\rc\](\a\vs4\al\c1(0，\f(π,2)))，,－cs x，x∈\b\lc\(\rc\](\a\vs4\al\c1(\f(π,2)，\f(3π,2)))，,3cs x，x∈\b\lc\(\rc\](\a\vs4\al\c1(\f(3π,2)，2π))，))x∈[0,2π]，
如图：
结合图象可得，当k∈(0,1)时，
直线y＝k与函数y＝f(x)的图象有四个不同的交点．x
0
eq \f(π,2)
π
eq \f(3π,2)
2π
2sin x
0
2
0
－2
0
2sin x－1
－1
1
－1
－3
－1
x
0
eq \f(π,2)
π
eq \f(3π,2)
2π
cs x
1
0
－1
0
1
－1－cs x
－2
－1
0
－1
－2