空间几何体外接球的五种模型-高考数学解答题复习课件PPT

这是一份空间几何体外接球的五种模型-高考数学解答题复习课件PPT，共8页。PPT课件主要包含了答案D，答案13π，答案C，答案A等内容，欢迎下载使用。
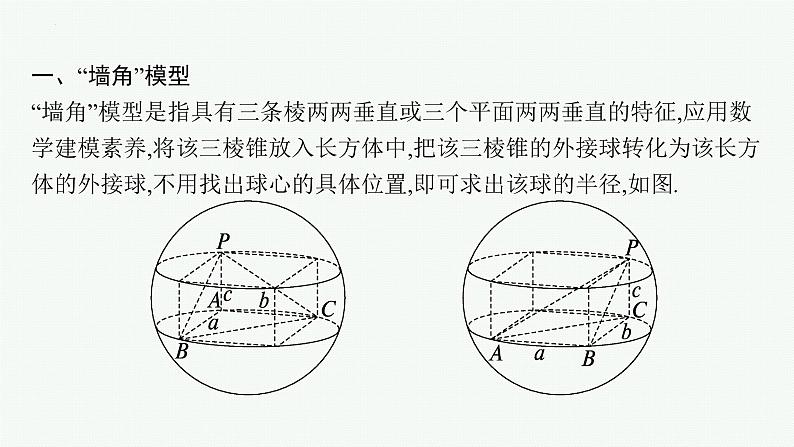
一、“墙角”模型“墙角”模型是指具有三条棱两两垂直或三个平面两两垂直的特征,应用数学建模素养,将该三棱锥放入长方体中,把该三棱锥的外接球转化为该长方体的外接球,不用找出球心的具体位置,即可求出该球的半径,如图.
例1已知三棱锥P-ABC的四个顶点在球O的球面上,PA=PB=PC,△ABC是边长为2的正三角形,E,F分别是PA,AB的中点,∠CEF=90°,则球O的体积为(　　)
规律方法 破解此类题的关键:一是“见数思形”,需在草稿纸上画出三棱锥的草图,判断是否有两两垂直的三条棱;二是“会构造”,即会构造长方体;三是“用公式”,4R2=a2+b2+c2(其中R为该三棱锥的外接球的半径,a,b,c为两两垂直的三条棱的长).
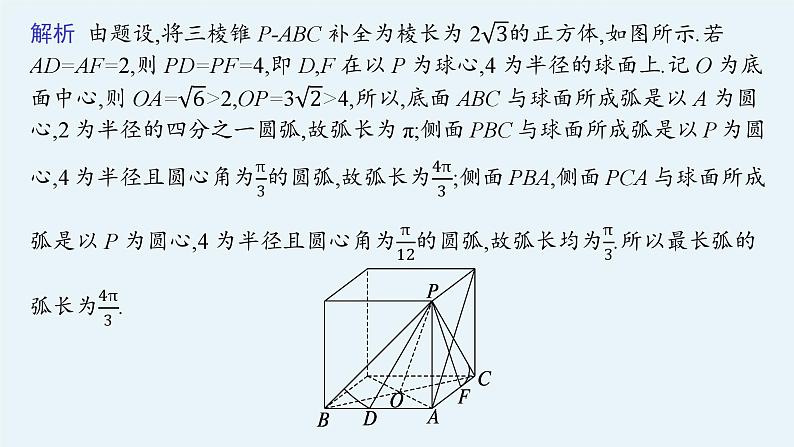
对点训练1(2022·广东广州一模)已知三棱锥P-ABC的棱AP,AB,AC两两互相垂直,AP=AB=AC=2 ,以顶点P为球心,4为半径作一个球,球面与该三棱锥的表面相交得到四段弧,则最长弧的弧长等于　　　　　. 
二、“对棱相等”模型“对棱相等”模型是指三棱锥的相对的两条棱相等,应用数学建模素养,构建长方体,将该三棱锥放入该长方体中,使三棱锥的顶点与长方体的顶点重合,将该三棱锥的外接球转化为该长方体的外接球,从而求出该外接球的半径,如图.
规律方法 破解此类题的关键:一是会翻折,即通过翻折,明确不变量与变化的量;二是会构造,即根据所给的相等对棱的长度,构造符合条件的长方体;三是会列出方程组,即设出长方体的长、宽、高,根据三棱锥的三对棱的长度,列出方程组,解方程组,即可求出所构造的长方体的共顶点的相邻的三条棱的长;四是用公式,利用长方体的体对角线长等于该三棱锥的外接球的直径,求出该三棱锥的外接球的半径,利用球的表面积与体积公式,即可得到外接球的表面积与体积.
对点训练2(2023·辽宁大连模拟)如图所示,在正四面体ABCD中,E是棱AD的中点,P是棱AC上一动点,BP+PE的最小值为 ,则该正四面体的外接球的表面积等于　　　　. 答案 12π
如图,将正四面体补成一个正方体,则正方体的棱长为2,则该正四面体的外接球的直径为正方体的体对角线长,所以2R=2 ,即R= ,故该正四面体的外接球的表面积S=4πR2=12π.
三、“汉堡”模型“汉堡”模型是指对于直棱柱,应用数学建模素养,结合球与直棱柱的有关性质,建立“汉堡”模型,上、下底面外接圆的圆心连线构成的线段的中点即为直棱柱外接球球心,球心到各个顶点的距离都等于外接球的半径,如图.
例3已知三棱柱的侧棱垂直于底面,所有棱的长都为6,顶点都在一个球面上,则该球的表面积为(　　)A.36πB.84πC.132πD.180π答案 B
规律方法 破解此类题的关键是画出草图,确定直三棱柱的外接球球心的位置为直三棱柱的上、下底面三角形外接圆的圆心连线所构成的线段的中点;二是利用正弦定理求出底面三角形的外接圆的半径,若是特殊三角形,如等边三角形或直角三角形,可利用特殊三角形的特点,快速获得其外接圆的半径;三是用定理,即利用勾股定理,求出球的半径;四是用公式,即利用球的表面积或体积公式求解,注意直三棱柱的外接球与内切球的本质区别.
对点训练3一个正六棱柱的底面是正六边形,其侧棱均垂直于底面.已知该六棱柱的顶点都在同一个球面上,六棱柱的体积为 ,底面周长为3,那么这个球的体积为　　　　　. 
四、“心有所依”模型“心有所依”模型是指对于圆锥、圆台、侧棱相等的棱锥等几何体,可得球心必在该几何体的高所在的直线上,或者在棱锥一个底面的高所在直线上,由此可把相关信息集中到某一个直角三角形内,利用勾股定理求解,如图.
例4已知三棱锥M-ABC的四个顶点均在表面积为32π的球面上, AB=BC=2 ,AC=4,则三棱锥M-ABC的体积的最大值为(　　)
规律方法 破解此类题的关键:一是确定球心O的位置,如例4,先确定底面三角形的外接圆的圆心Q,则M,O,Q三点共线;二是计算出三棱锥底面外接圆的半径;三是利用勾股定理,即可求出球心到底面的距离,从而求出三棱锥的高.
五、“双心”模型“双心”模型:无法利用上面四种模型求解的问题,可利用球心、三角形(或四边形等)外接圆的圆心以及外接圆与球的交点所构成的直角三角形进行破解,如图.
例5已知三棱锥D-ABC的四个顶点在球O的球面上,若AB=AC=BC=DB=DC=1.当三棱锥D-ABC的体积取到最大值时,球O的表面积为(　　)
解析 如图,当三棱锥D-ABC的体积取到最大值时,则平面ABC⊥平面DBC,取BC的中点G,连接AG,DG,则AG⊥BC,DG⊥BC.分别取△ABC与△DBC的外心E,F,分别过点E,F作平面ABC与平面DBC的垂线,相交于点O,则点O为四面体ABCD的球心.由AB=AC=BC=DB=DC=1,得
规律方法 对一般棱锥来讲,外接球球心到各顶点的距离相等,当问题难以考虑时,可减少点的个数进行考虑,如先考虑到三个顶点的距离相等的点是三角形的外心,球心一定在过此点与此平面垂直的直线上.