初中数学苏科版七年级下册7.2 探索平行线的性质教学ppt课件

这是一份初中数学苏科版七年级下册7.2 探索平行线的性质教学ppt课件，共34页。PPT课件主要包含了学习目标，问题情景1，问题情景2，知识回顾，同位角，内错角，同旁内角，∠1∠2，同位角相等两直线平行，∠3∠2等内容，欢迎下载使用。
1.通过对基本图形的操作、观察，得出两直线平行的性质，会用平行线的性质进行简单说理；2.在复习、比较平行线的性质和判定的基础上，能正确区分平行线的性质和判定，并能运用平行线的性质和判定进行计算和说理．
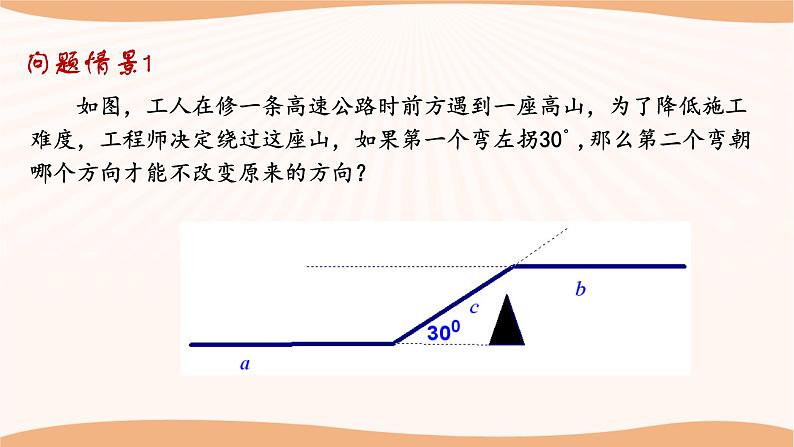
如图，工人在修一条高速公路时前方遇到一座高山，为了降低施工难度，工程师决定绕过这座山，如果第一个弯左拐30°,那么第二个弯朝哪个方向才能不改变原来的方向？
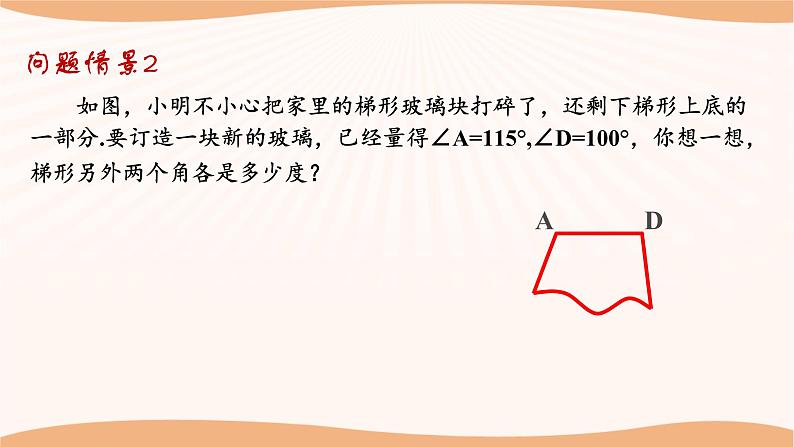
如图，小明不小心把家里的梯形玻璃块打碎了，还剩下梯形上底的一部分.要订造一块新的玻璃，已经量得∠A=115°,∠D=100°，你想一想，梯形另外两个角各是多少度？
判定两条直线平行的方法是什么？
同旁内角互补两直线平行
反过来,如果两条直线平行,同位角、内错角、同旁内角各有怎样的数量关系呢?
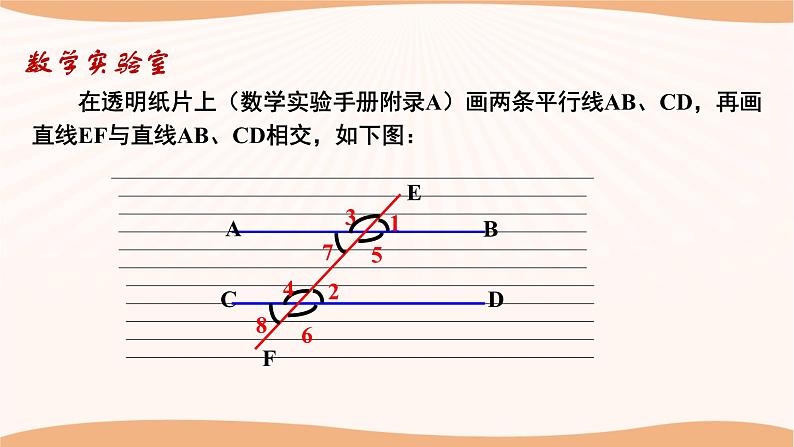
在透明纸片上（数学实验手册附录A）画两条平行线AB、CD，再画直线EF与直线AB、CD相交，如下图：
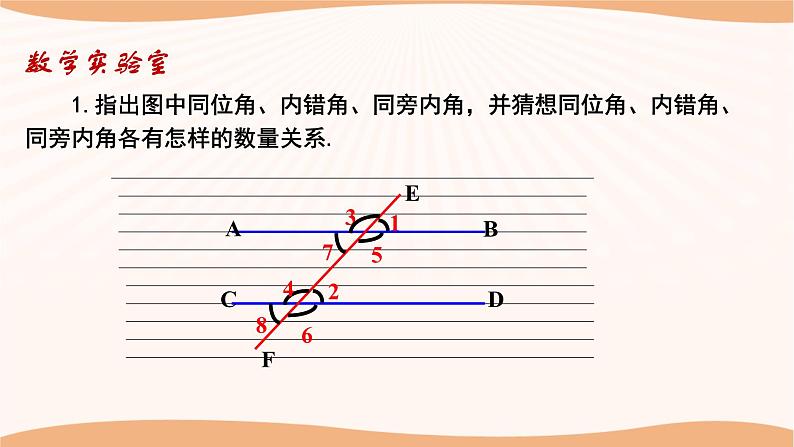
1.指出图中同位角、内错角、同旁内角，并猜想同位角、内错角、同旁内角各有怎样的数量关系.
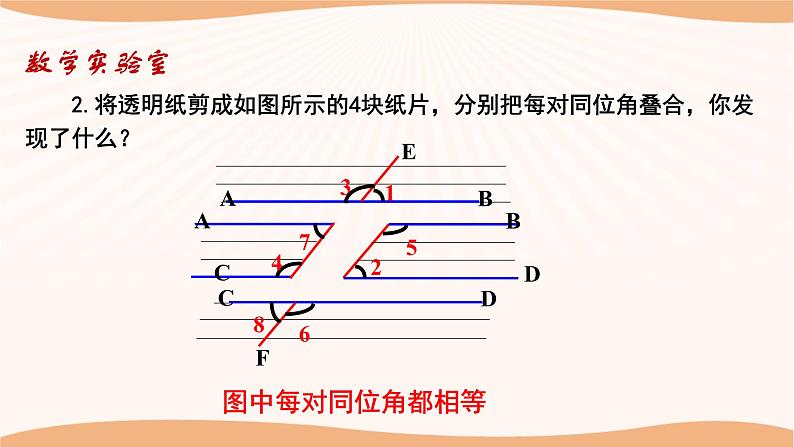
2.将透明纸剪成如图所示的4块纸片，分别把每对同位角叠合，你发现了什么？
平行线的性质1：“两条平行直线被第三条直线所截,同位角相等．” 简称： “两直线平行，同位角相等.”
直线a、b被直线c所截， ∵a∥b∴∠1=∠2（两直线平行，同位角相等）
3.再把剪开得到的每对内错角重叠,你发现了什么？
根据两直线平行,同位角相等，你能说明“两直线平行,内错角相等”成立的理由吗?
（两直线平行,同位角相等）
平行线的性质2：“两条平行直线被第三条直线所截,内错角相等．” 简称： “两直线平行，内错角相等.”
直线a、b被直线c所截， ∵a∥b ∴∠2=∠3（两直线平行，内错角相等）
4.再把剪开得到的每对同旁内角拼起来,你又发现了什么？
图中每对同旁内角都互补
如果我们现在只知道两直线平行,同位角相等.你能说明两直线平行,同旁内角互补”成立的理由吗?
又∵∠1+∠4=180°
∴∠2+∠4=180°
平行线的性质3：“两条平行直线被第三条直线所截,同旁内角互补．” 简称： “两直线平行，同旁内角互补.”
直线a、b被直线c所截， ∵a∥b∴∠2+∠4=180°（两直线平行，同旁内角互补）
两直线平行同旁内角互补
你能说出平行线的性质和平行线的判定方法的区别和联系吗?
例1:如图,已知直线a∥b,∠1 = 50°, 求∠2的度数.
∴∠ 2= 50 ° (等量代换)
解：∵ a∥b(已知)
∴∠ 1= ∠ 2 (两直线平行,内错角相等)
又∵∠ 1 = 50 ° (已知)
变式1:如图,已知直线a∥b,∠1 = 50°, 求∠3，∠4的度数 .
∴∠ 3= 50 ° (等量代换)
∴∠ 1= ∠ 3 (两直线平行,同位角相等)
又∵∠3+∠4=180°(邻补角定义)
∴∠ 4=180°-∠3 =180°- 50 ° = 130 ° (等式性质)
在如图所示的“三线八角”中，若a∥b，你至少要知道几个角的度数，可以求出另外的角的度数？
当两条平行线被第三条直线所截时，只要知道其中的1个角，就能求出“三线八角”中的另7个角.
解：第二个弯朝向右转30°才能不改变原来的方向.
解：∵AD//BC （已知）， ∴A＋B＝180°， （两直线平行，同旁内角互补） 　即 B＝180 °－A＝180 °－115 °＝65 °， ∵AD//BC（已知） ， ∴D＋C＝180 °， （两直线平行，同旁内角互补）　　即C＝180 °－D＝180 °－100 °＝80 °．答：梯形的另外两个角分别为65 °、80 °．
变式2:如图,已知∠3 =∠4，∠1 = 50°, 求∠2的度数 .
解：∵ ∠ 3= ∠ 4(已知)
∴ a∥b (同位角相等，两直线平行)
∴∠ 1=∠2(两直线平行，同位角相等)
平行线的性质和平行线的判定同时使用
例2:如图，AB∥CD, AF∥DE，试说明∠A=∠D.
∠A＝∠BED（两直线平行，内错角相等），
∴∠A＝∠D （等量代换）.
∵ AB∥CD，AF∥ED（已知），
变式:如图，AB∥CD, ∠A=∠D，判断AF与ED的位置关系，并说明理由.
∴∠D＝∠BED（两直线平行，内错角相等），
又∵∠A＝∠D （已知），
∴∠A＝∠BED （等量代换） ，
∴AF∥ED（同位角相等，两直线平行）．
∵ AB∥CD（已知），
1.如图，如果∠BAC=∠ACD，那么根据__________________可得___∥___,从而进一步根据_____________________ ,可得∠B+∠_____=180°
内错角相等,两直线平行
两直线平行,同旁内角互补
2.已知：如图，AB∥CD，∠1＝∠2，则GP与QH的位置关系是什么？ 并说明理由．
解：GP∥QH.理由如下：∵AB∥CD，∴∠EGB=∠EHD.(两直线平行，同位角相等)又∵∠1=∠2， ∠EGP=∠EGB-∠1， ∠EHQ=∠EHD-∠2，∴∠EGP=∠EHQ，(等式的性质)∴GP∥HQ.(同位角相等,两直线平行)
回顾本节课的学习，你有哪些收获：
2.平行线的性质和平行线的判定方法的区别和联系.
同位角相等内错角相等同旁内角互补
1.如图，若AB ∥ CD,则下列结论中 ① ∠B=∠2 ② ∠3=∠A ③ ∠3=∠B ④ ∠B + ∠BCD= 180°正确的是 ( )
A .① ② B. ① ③
C .① ④ D .③ ④
2.如图在四边形ABCD中,已知AB∥CD,∠B = 60°.①求∠C的度数;②由已知条件能否求得∠A的度数?
解: ① ∵ AB∥CD(已知), ∴∠B + ∠C= 180° (两直线平行,同旁内角互补), 又∵∠B = 60° (已知), ∴∠C ＝180 °－∠B ＝180 °－60 ° ＝120° (等式的性质).
3.已知，如图，AC∥DE，CD∥EF，试说明：∠1＝∠2
4.如图,AB∥CD,FE平分∠GFD,若∠GHA=40°求∠BEF.
5.阅读下列解题过程，然后解答后面的问题．如图①，已知AB∥CD，∠B＝35°，∠D＝32°，求∠BED的度数．解：如图①，过点E作EF∥AB，则∠1＝∠B＝35°.因为AB∥CD，所以CD∥EF，所以∠2＝∠D＝32°.所以∠BED＝∠1＋∠2＝35°＋32°＝67°.