第七章 平面图形的认识（二）（小结思考）（课件）-2022-2023学年七年级数学下册同步精品课件（苏科版）

这是一份第七章 平面图形的认识（二）（小结思考）（课件）-2022-2023学年七年级数学下册同步精品课件（苏科版），共34页。

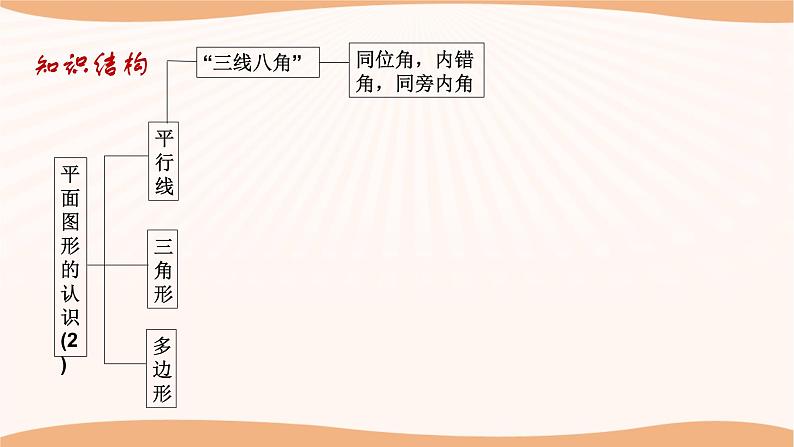
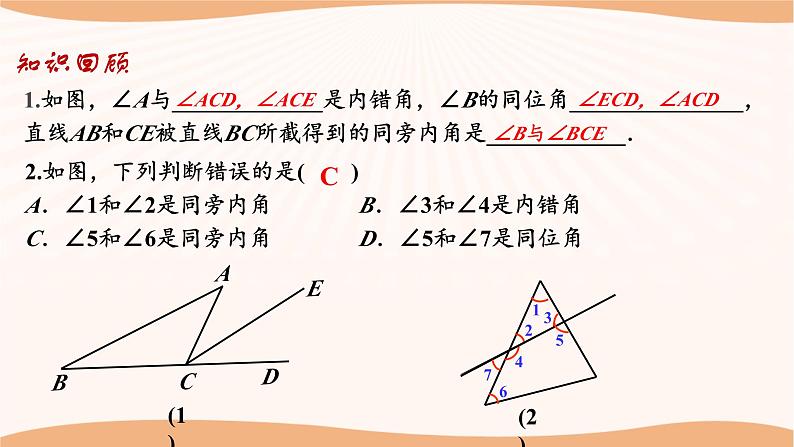
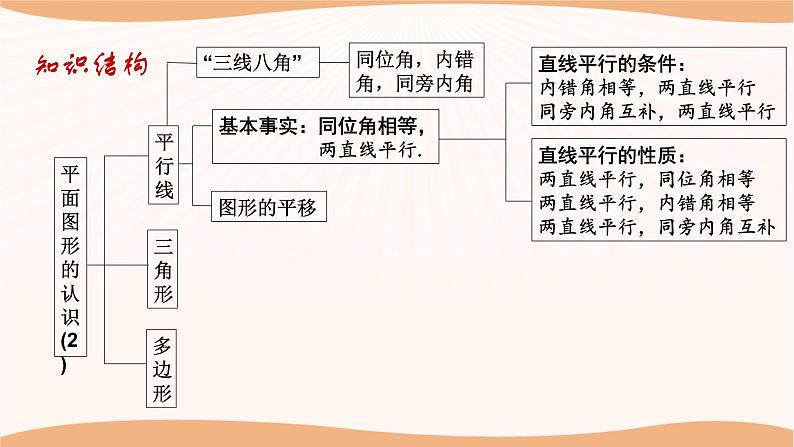
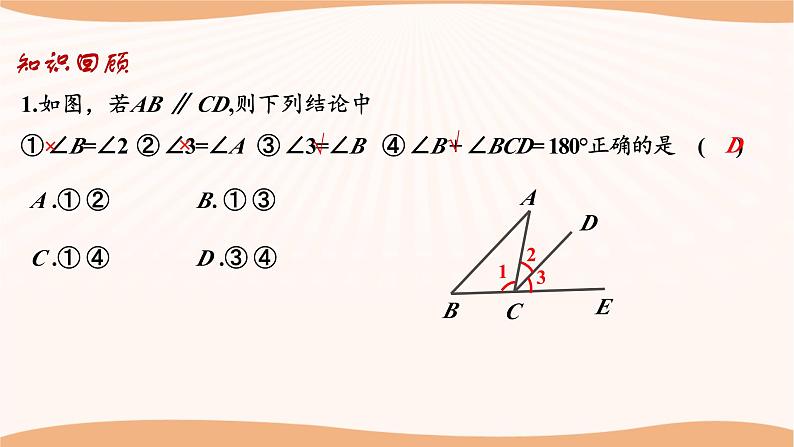
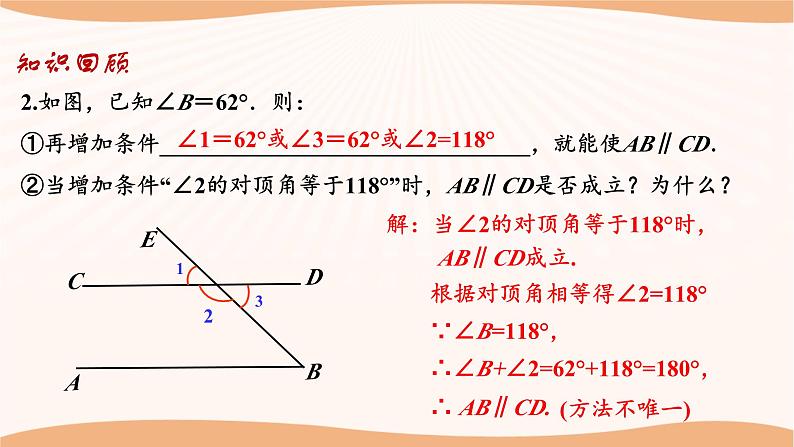
1.回顾、思考本章所学知识及思想方法，并能用自己喜欢的方式进行梳理，使所学知识系统化；2.进一步丰富对平面图形的认识，能有条理地、清晰地阐述自己的观点.学习目标知识结构平面图形的认识 (2)平行线三角形多边形“三线八角”同位角，内错角，同旁内角知识回顾同位角、内错角和同旁内角的识别方法：12345678被截线之间被截线之间被截线同侧截线同旁截线两旁截线同旁FZU知识回顾1.如图，∠A与_____________是内错角，∠B的同位角_______________，直线AB和CE被直线BC所截得到的同旁内角是____________．∠ACD，∠ACE∠ECD，∠ACD∠B与∠BCE(1)(2)2.如图，下列判断错误的是(　　)A．∠1和∠2是同旁内角 B．∠3和∠4是内错角C．∠5和∠6是同旁内角 D．∠5和∠7是同位角C知识结构平面图形的认识 (2)平行线三角形多边形基本事实：同位角相等， 两直线平行.直线平行的条件：内错角相等，两直线平行同旁内角互补，两直线平行直线平行的性质：两直线平行，同位角相等两直线平行，内错角相等两直线平行，同旁内角互补“三线八角”同位角，内错角，同旁内角图形的平移1.如图，若AB ∥ CD,则下列结论中 ① ∠B=∠2 ② ∠3=∠A ③ ∠3=∠B ④ ∠B + ∠BCD= 180°正确的是 ( )A .① ② B. ① ③C .① ④ D .③ ④D×√×√知识回顾2.如图，已知∠B＝62°．则：①再增加条件________________________________，就能使AB∥CD． ②当增加条件“∠2的对顶角等于118°”时，AB∥CD是否成立？为什么？知识回顾∠1＝62°或∠3＝62°或∠2=118°2解：当∠2的对顶角等于118°时， AB∥CD成立.根据对顶角相等得∠2=118°∵∠B=118°，∴∠B+∠2=62°+118°=180°，∴ AB∥CD.(方法不唯一)知识回顾②若∠BAE=60°,∠AEB=98°，则∠DCF= °，∠CFD= °.3.如图，△ABE向右平移一定距离后得到△CDF.①图中存在平行且相等的三组线段是AB和____，AE和____，AC和_______.CDCFBD或EF60°98°6098BAEDCF知识回顾4.如图，在长方形ABCD中，AC与BD相交于点O，画出三角形AOB平移后得到的图形，其平移方向为射线AD的方向，平移的距离为线段AD的长．平移作图的步骤：定、找、移、连.①定：确定平移的方向和距离;②找：找出表示图形的关键点;③移：过关键点作平行且相等的线段，得到关键点的对应点;④连：按原图形顺次连接对应点.知识结构平面图形的认识 (2)平行线三角形多边形三边关系两边之和大于第三边特殊线段角平分线中 线 高三角形3个内角的和等于180°2.现有两根木棒,它们的长度分别为20cm和30cm,若不改变木棒的长度, 要钉成一个三角形木架,应在下列四根木棒中选取 ( ) A.10cm的木棒 　B.20cm的木棒 　C.50cm的木棒 　D.60cm的木棒B1.三条线段的长度分别为：①3、8、10 ②5、2、7 ③5、5、11 ④13、12、20能组成三角形的有( )组.B知识回顾知识回顾3.如图，在△ABC中，∠A＝70°，∠C＝30°，BD平分∠ABC交AC于点D，DE∥AB，交BC于点E，则∠BDE的度数是(　　) A．30° B．40° C．50° D．60°B知识回顾4.如图，作出△ABC中AC边上的高，∠ABC的平分线，BC边上的中线.平面图形的认识 (2)平行线三角形多边形n边形的内角和等于(n-2)180°n边形的外角和等于360°知识结构知识回顾 一个多边形的内角和比它的外角和的3倍少180°,求这个多边形的边数．解：设这个多边形的边数是n，由题意得(n－2)×180°＝3×360°－180°，解得n＝7，∴这个多边形的边数是7.例题讲解一、分类讨论思想例1.若长度分别为3、6、x的3条线段搭成一个三角形.（1）x的取值范围是___________;（2）若x为偶数，那么一共可以构成____个不同的三角形； （3）若这个三角形是等腰三角形，那么x=_____,三角形周长为_______.3＜x＜93615巩固练习1.若长度分别是4、7、x的3条线段能搭成一个三角形. ①x的取值范围是___________;②若x为奇数，那么一共可以构成______个不同的三角形;③若这个三角形是等腰三角形，那么x=_______，三角形周长为________.3＜x＜1134或715或182.若等腰三角形ABC周长为26，AB=6,求它的腰长.巩固练习3.等腰三角形ABC一腰AB上的中线CD把三角形的周长分成6cm和9cm的两部分，求等腰三角形的三边长．解：设底边长为x cm，①当BD＋BC＝6cm时，BD＝(6－x)cm，∴2(6－x)＋(6－x)＝9，解得x＝3，此时，三角形的三边长为6 cm，6 cm，3 cm，满足三角形的三边关系；②当BD＋BC＝9 cm时，BD＝(9－x)cm，∴2(9－x)＋(9－x)＝6，解得x＝7，此时，三角形的三边长为7 cm，4 cm，4 cm，满足三角形的三边关系．综上，等腰三角形的三边长为6 cm，6 cm，3 cm或7 cm，4 cm，4 cm.例题讲解二、数形结合思想例2.如图，∠1与∠2互补，∠1=∠BAD，试说明：AD∥EF.FG12解：∵ ∠1与∠2互补，∴∠1＋∠2＝180°，∵ ∠1＝∠BAD，∴∠BAD＋∠2＝180°，∴AD∥EF.例题讲解二、数形结合思想FG12变式1：如图， AD∥EF， ∠1=∠BAD ，试说明： ∠1与∠2互补.解：∵AD∥EF，∴∠BAD＋∠2＝180°，∵ ∠1＝∠BAD，∴∠1＋∠2＝180°，∴∠1与∠2互补.例题讲解二、数形结合思想变式2：如图，EF⊥BC，AD是△ABC的高，∠1=∠BAD ，试说明：∠1+∠2=180°FG1∟∟2解： ∵ EF⊥BC，AD是△ABC的高，∴∠BFE=∠BDA=90°，∴AD∥EF，∴∠BAD＋∠2＝180°，∵ ∠1＝∠BAD，∴∠1＋∠2＝180°.例题讲解二、数形结合思想FG13∟∟2变式3：如图，EF⊥BC，AD是△ABC的高， ∠2+∠3=180° ，试说明：∠CGD=∠BAC解： ∵ EF⊥BC，AD是△ABC的高，∴∠BFE=∠BDA=90°,∴AD∥EF，∴∠BAD＋∠2＝180°，∵ ∠2+∠3=180°，∴∠3＝∠BAD，∴DG∥AB，∴ ∠CGD=∠BAC.巩固练习1.如图，BD是∠ABC的平分线，ED∥BC，∠FED＝∠BDE，则EF也是∠AED的平分线．完成下列推理过程．F解：∵BD是∠ABC的平分线(________)，∴∠ABD＝∠DBC(______________)．∵ED∥BC(________)，∴∠BDE＝∠DBC( __________________ )，∴________________(__________)．又∵∠FED＝∠BDE(________)，∴________( __________________ )，∴∠AEF＝∠ABD( __________________ )，∴∠AEF＝∠FED(________)，∴EF是∠AED的平分线(____________)．已知角平分线的定义已知两直线平行，内错角相等∠ABD＝∠BDE等量代换已知EF∥BD内错角相等，两直线平行两直线平行，同位角相等等量代换角平分线的定义巩固练习2.如图所示,AD,AE分别是△ABC的高和角平分线.(1)∠B＝30°,∠C＝70°,求∠DAE的度数． 巩固练习2.如图所示,AD,AE分别是△ABC的高和角平分线.(2)△ABC中，若∠B=α，∠C=β（α＜β），请你根据（1）的结果猜想 ∠DAE与α，β间的等量关系，并说明理由． 例题讲解三、由特殊到一般思想：探索：从n(n≥3）边形的一个顶点出发能画出多少条对角线？n边形一共有多少条对角线？00122539520n-3… 巩固练习 变式1：一个多边形过顶点剪去一个角后，内角和没变小且所得多边形的内角和为720°，则原多边形的边数是________． 一多边形过顶点剪去一个角后，所得多边形的内角和为720°，则原多边形的边数是________．6或76 变式2：一个多边形剪去一个角后，所得多边形的内角和为720°，则原多边形的边数是________．5或6或71.如图，三角形的个数是（ ）个 .A．3 B．4 C．5 D．6C课后检测2.下列说法不正确的是(　　)A．三角形的三条高线交于一点 B．直角三角形有三条高C．三角形的三条角平分线交于一点 D．三角形的三条中线交于一点A3.下列各图中，正确画出AC边上的高的是(　　)DABCD4.如图，在△ABC中，∠BAC＝90°，AB＝3cm，AC＝4cm，把△ABC沿着直线BC向右平移2.5cm后得到△DEF，连接AE，AD，有以下结论：①AC∥DF；②AD∥CF；③CF＝2.5cm；④DE⊥AC.其中正确的结论有(　　) A．1个 B．2个 C．3个 D．4个D课后检测5.如图，AB∥CD，点E，F在AC上，已知∠CED＝70°，∠BFC＝130°，则∠B＋∠D的度数为(　　) A．40° B．50° C．60° D．70°CMN课后检测CBADEF解：如图，设ED，FB的交点为点G，过点G作MN∥CD交AC于M.根据题意得∠CED＝70°，∠BFC＝130°，∴∠EFG＝50°，∴∠EGF＝180°－50°－70°＝60°.易知MN∥CD∥AB，∴∠B＝∠BGN，∠D＝∠DGN，∴∠B＋∠D＝∠BGN＋∠DGN＝∠BGD.∵ED，BF相交于点G，∴∠EGF＝∠BGD＝60°，∴∠B＋∠D＝60°.课后检测 90°50°30°60°90°7.如图，在△ABC中，∠A、∠B的平分线相交于点，若∠C＝70°，则∠AIB＝_____;若∠AIB＝155°,则∠C＝_____.125°130°8.若Δ???的三边分别是?,?,?,则化简|?+?−?|−|?−?−?|的结果是_______.2b-2c课后检测9. 在△ABC中，∠A=n°（1）设∠B、∠C的平分线交于点O，求∠BOC的度数；（2）设△ABC的外角∠CBD、∠BCE的平分线交于点O′,求∠BO′ C的度数；（3）∠BOC与∠BO′ C有怎样的数量关系？课后检测10.如图（1），△ABC是一个三角形的纸片，点D、E分别是△ABC边上的两点，将∠A沿DE折叠后，点A的对应点记为A′.（1）若点A’落在AC边上，则∠BDA′与∠A的关系是_____________．（2）如果折成图2的形状，猜想∠BDA′、∠CEA′和∠A的关系，并说明理由．（3）如果折成图3的形状，猜想∠BDA′、∠CEA′和∠A的关系，并说明理由．图1图2图3