苏科版七年级下册第12章 证明12.2 证明多媒体教学课件ppt

这是一份苏科版七年级下册第12章 证明12.2 证明多媒体教学课件ppt，共9页。PPT课件主要包含了学习目标，知识结构，互逆命题，命题的结构，命题的分类，真命题，假命题，已知事项，由已知事项推出的事项，判断一件事情的句子等内容，欢迎下载使用。
1. 了解定义、命题、定理、逆命题、互逆命题等概念；2.会区分命题的条件和结论.会判断一个命题的真假.会写出一个命题的逆命题，并知道如果一个命题是真命题，它的逆命题不一定是真命题；3.通过具体的例子理解反例的作用；4. 理解证明的必要性，掌握证明的格式.
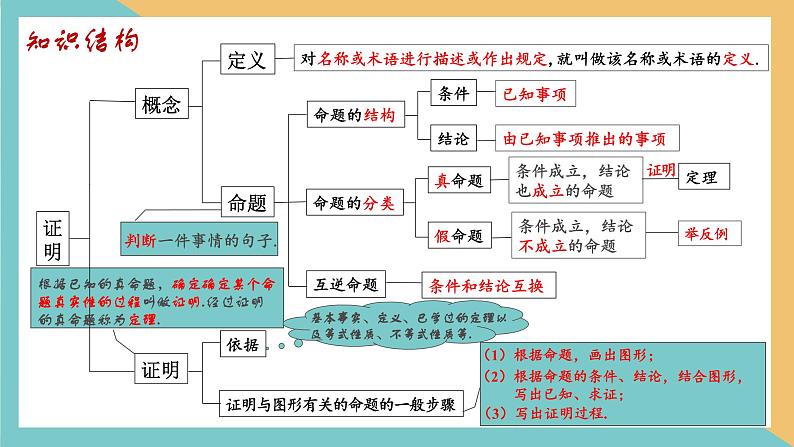
对名称或术语进行描述或作出规定,就叫做该名称或术语的定义.
条件成立，结论也成立的命题
条件成立，结论不成立的命题
证明与图形有关的命题的一般步骤
（1）根据命题，画出图形；
（2）根据命题的条件、结论，结合图形， 写出已知、求证；
根据已知的真命题，确定确定某个命题真实性的过程叫做证明.经过证明的真命题称为定理.
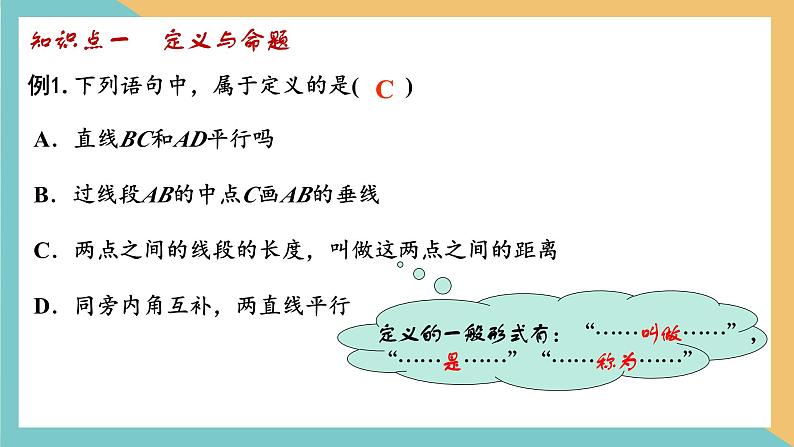
知识点一 定义与命题
例1. 下列语句中，属于定义的是(　　)
A．直线BC和AD平行吗B．过线段AB的中点C画AB的垂线C．两点之间的线段的长度，叫做这两点之间的距离D．同旁内角互补，两直线平行
例2. 下列语句中，属于命题的是(　　)
A．同角的余角相等B．过点A作直线MNC．∠1＝∠2吗D．取线段AB的中点
命题的特征：是句子、有判断(只需作出判断、无关对错.)注意：疑问句、祈使句、命令句、感叹句等不是命题.
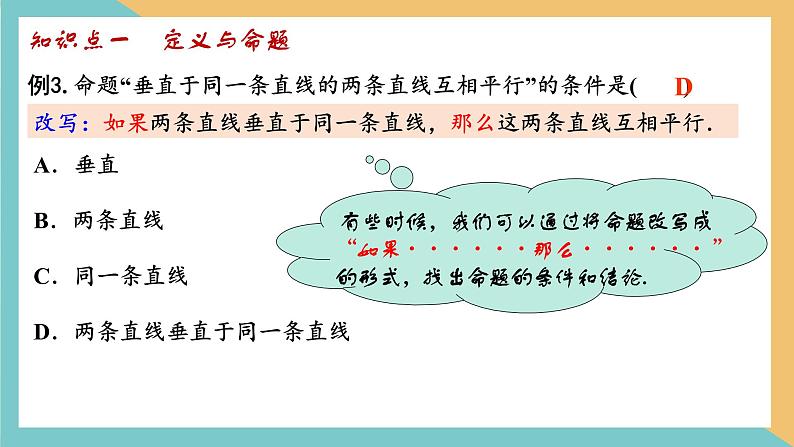
例3. 命题“垂直于同一条直线的两条直线互相平行”的条件是(　　)
A．垂直B．两条直线C．同一条直线D．两条直线垂直于同一条直线
改写：如果两条直线垂直于同一条直线，那么这两条直线互相平行．
例4. 下列命题中，属于假命题的是(　　)
A．对顶角相等B．同位角相等C．两点确定一条直线D．n边形(n≥3)的内角和是(180n－360)°
判断一个命题是假命题只需举出一个反例.使之具有命题的条件，而不具有命题的结论.
例5. 说出下列命题的逆命题，并判定原命题和逆命题的真假：
( )
(1)轴对称图形是等腰三角形；
逆命题：等腰三角形是轴对称图形.
(2)同角的补角相等.
逆命题：如果两个角相等，那么这两个角是同一个角的补角.
把一个命题的条件和结论互换就得到它的逆命题，每个命题都有逆命题.原命题是真命题，它的逆命题不一定是真命题.
1. 下列命题中，属于真命题的是(　　)
A．内错角相等B．若a10＝b10，则a＝bC．任意多边形的内角和为360°D．等角的补角相等
2. 能说明命题“对于任何数a，|a|＞－a”是假命题的一个反例可以是(　　)
3. “两负数的商为正数”的条件是___________，结论是_____________⁠； 
4. 改写命题“等角的补角相等”:如果_________，那么_______________. 
(2) 如果(1)中的逆命题不是真命题，请你添加一个条件使之成为真命题，写出这个真命题.
解:(1)不是真命题. 反例：a=1，b=-2时，a＞b，那么|?|＜|?|
解:(2) 如果a＞b且a、b是非负数，那么|?|＞|?|.
（5）平行于同一条直线的两条直线平行.
（3）直角三角形的两个锐角互余.
（4）有两个角互余的三角形是直角三角形.
（2）三角形的外角等于与它不相邻的两个内角的和.
（1）三角形三个内角的和等于180°.
例6. 探索两个连续奇数的平方差的规律，并加以证明.
设n为整数，两个连续奇数分别为2n-1、2n+1,∵(2n+1)2-(2n-1)2=[(2n+1)+(2n-1)] [(2n+1)-(2n-1)]=8n
解：两个连续奇数的平方差能被8整除.
∴两个连续奇数的平方差能被8整除.
例7. 证明：两直线平行，同旁内角互补．
（二）证明与图形有关的命题的一般步骤
（2）根据命题的条件、结论，结合图形， 写出已知、求证；
已知：AB∥CD；求证：∠1 + ∠2 = 180°；
证明：∵ AB∥CD（已知）,∴ ∠2＝∠3（两直线平行，同位角相等）， ∵ ∠1＋∠3＝180°（平角的定义），∴ ∠1＋∠2＝180°（等量代换）．
例8. 已知:AB∥CD，求证:∠A+∠C+∠AEC=360°.
证明：过E点作EF∥AB，则∠A+∠1=180°（两直线平行平行，同旁内角互补） ∵AB∥CD（已知）∴EF∥CD（平行于同一直线的两直线互相平行）∴∠2+∠C=180°（两直线平行平行，同旁内角互补）∴∠A+∠1+∠2+∠C=360°（等式的基本性质）即∠A+∠C+∠AEC=360°
（三）与平行线的判定与性质相关的证明
变式1: 如图，AB∥CD，试用不同的方法证明∠AEC=∠A+∠C.
变式2: 如图，AB∥CD， ∠AEC与∠A、∠C 之间有怎样的数量关系？证明你的结论.
∠AEC=∠A-∠C
变式3: 如图甲:已知AB∥DE，那么∠1+∠2+∠3等于多少度?试加以说明. 当已知条件不变,而图形变为如图乙时,结论改变了吗? 图丙中的∠1+∠2+∠3+∠4是多少度呢？如果如丁图所示，∠1+∠2+∠3+…+∠n的和又为多少度？你找到了什么规律吗？
∠1+∠2+∠3=2×180°
∠1+∠2+∠3+∠4=3×180°
∠1+∠2+∠3+∠4+……+∠n=(n-1)×180°
（四）与三角形内角和定理相关的证明
例9: 将例8变式1的图中直线AB绕点A顺时针方向旋转一定角度交直线CD于点Q ，如下图，则∠AEC 、 ∠A、 ∠C、∠AFC 之间有何数量关系？
∠AEC= ∠A+∠C+∠AFC
变式1：在五角星ABCDE中，∠A、∠B、∠C、∠D、∠E的和等于多少度？请加以证明.
解：易证 ∠1+∠2=∠B+∠E∵在△ACD中， ∠ A+∠ACD+∠ADC =180°∴∠A+∠ACE+∠1+∠2+∠ADB=180°即:∠A+ ∠B+ ∠C+ ∠D+ ∠E=180°
你还能想到其他证明方法吗？试一试 .
变式2：把图1、图2叫蜕化的五角星，问它们的五角之和与五角星图形的五角之和仍相等吗？为什么？
变式3：如图：求∠A+ ∠B+ ∠C+ ∠D+ ∠E+∠F的度数.
∠A+ ∠B+ ∠C+ ∠D+ ∠E+∠F=360°
1.下列关于判断一个数学结论是否正确的叙述中，正确的是(　 )
B. 只需依靠经验获得
D. 必须进行有根据的推理
2.下列平行线的判定方法中，是基本事实的是(　　)A．同旁内角互补，两直线平行B．同位角相等，两直线平行C．内错角相等，两直线平行D．在同一平面内，不相交的两条直线叫做平行线
3.如图，OP∥QR∥ST，则下列各式中正确的是( ). A．∠1＋∠2＋∠3＝180° B．∠1＋∠2－∠3＝90° C．∠1－∠2＋∠3＝90° D．∠2＋∠3－∠1＝180°
4. 如图，AB∥CD，EF⊥CD于点F.若∠BEF＝150°，则∠ABE的度数为 　60°　⁠. 
5. 将一副三角尺按如图所示的方式摆放，且AB∥CD，则∠1的度数为 　105　⁠. 
6. 如图所示为可调躺椅示意图，AE与BD的交点为C，且∠A、∠B、∠E保持不变.为了舒适，需调整∠D的大小，使∠EFD＝110°，则图中∠D应 　减少　⁠(填“增加”或“减少”) 　10°　⁠. 
7. 如图，AB∥DE，且∠1＝∠2，∠3＝∠4.求证:BC∥EF.
(1) 证明:∵ AB∥DE(已知)，
∴ ∠1＝∠3( 　两直线平行，同位角相等　⁠). 
∵ ∠1＝∠2，∠3＝∠4(已知)，
∴ ∠2＝ 　∠4　⁠(等量代换). 
∴ BC∥EF( 　同位角相等，两直线平行　⁠). 
(2) 上述推理过程中，运用的互逆的真命题是　“两直线平行，同位角相等”和“同位角相等，两直线平______　⁠. 
两直线平行，同位角相等
同位角相等，两直线平行
“两直线平行，同位角相等”
和“同位角相等，两直线平行”
8. 已知：如图，EF∥AD，∠1＝∠2，∠BAC=70°.求∠AGD.
解：∵EF∥AD(已知)，∴∠2＝∠3(两直线平行，同位角相等)．∵∠1＝∠2(已知)，∴∠1＝∠3(等量代换)，∴DG∥AB(内错角相等，两直线平行)．∴ ∠BAC+ ∠AGD=180° (两直线平行，同旁内角互补)∵∠BAC=70° (已知) ，∴ ∠AGD=110° (等式性质) .
9.如图，在△ABC中，∠ACB=90°，AE是角平分线，CD是高，AE、CD相交于点F.求证： ∠CFE= ∠CEF
证明：在△ACE、 △ADF中，∵∠ACB=∠ADF=90°(已知)，∴∠CAE+ ∠CEF＝90° 、∠DAF+ ∠AFD＝90° (直角三角形的两个锐角互余).∵AE是角平分线(已知) ，∴ ∠ CAE =∠ DAF (角平分线定义)∴ ∠CEF = ∠ AFD(等式性质) .∵ ∠CFE = ∠ AFD(对顶角相等) ，∴ ∠CFE= ∠CEF (等量代换) .