精品解析：河南省郑州中原一中实验学校2021-2022学年八年级上学期期末数学试题（原卷版）

这是一份精品解析：河南省郑州中原一中实验学校2021-2022学年八年级上学期期末数学试题（原卷版），共20页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（每小题3分，共30分）
1. 下列各数中是无理数的是（ ）
A. B. -0.66C. D.
【答案】A
【解析】
【分析】根据无理数的定义解答即可．
【详解】解：A、是无理数，故此选项符合题意；
B、-0.66是有限小数，属于有理数，故此选项不符合题意；
C、是分数，属于有理数，故此选项不符合题意；
D、=5，5是整数，属于有理数，故此选项不符合题意．
故选：A．
【点睛】本题主要考查了无理数的定义，注意带根号的要开不尽方才是无理数，无限不循环小数为无理数.如π，，（每两个8之间依次多1个0）等形式都是无理数．
2. 七年级手工小组用彩带给如图所示的图片制作边框，已知AB=5，BC=12，则制作一个边框需要彩带的长度是（ ）
A 5B. 12C. 13D. 30
【答案】D
【解析】
【分析】由勾股定理可算出AC的长度，进而可得到答案．
【详解】解：在Rt△ABC中，，
故制作边框需要的彩带长度为：13+12+5=30，
故选：D．
【点睛】本题考查勾股定理的实际应用，能够熟练运用勾股定理是解决本题的关键．
3. 在平面直角坐标系中，点M在第四象限，到x轴、y轴的距离分别为4和3，则点M的坐标为（ ）
A. （4，-3）B. （3，-4）C. （-3，4）D. （-4，3）
【答案】B
【解析】
【分析】根据点M在第四象限，则有点M的横坐标大于0，纵坐标小于0，进而根据到坐标轴的距离求解即可．
【详解】由点M在第四象限，则有点M的横坐标大于0，
纵坐标小于0，点M到x轴、y轴的距离分别为4、3，
所以点M的坐标为；
故选B．
【点睛】本题主要考查平面直角坐标系点的坐标，熟练掌握各象限的点坐标特点求点的坐标是解题的关键．
4. 一副三角尺如图所示摆放，∠α 的大小为（ ）度
A. 90B. 100C. 105D. 120
【答案】C
【解析】
【分析】过点G作，根据直角三角形的性质分别求出∠A、∠E，由题意证明，易得，再根据平行线的性质计算，得到答案．
【详解】解：如图，过点G作，
由题易得：∠E＝90°−45°＝45°，
∠A＝90°−30°＝60°，，
∵∠F=∠FIB=90°，
∴，
∵
∴
∴∠EGH=∠E=45°，∠AGH=∠A=60°，
∴∠α＝45°＋60°＝105°，
故选：C．
【点睛】本题考查了平行线的性质与判定、直角三角形的性质，作出辅助线是解题的关键．
5. 下列命题是真命题的是（ ）
A. 是一组勾股数
B. 同旁内角互补
C. 在一次函数y= -3x+2中，y随x的增大而增大
D. 若，则y+x=-3
【答案】D
【解析】
【分析】根据勾股数的定义、平行线的性质、一次函数的性质以及非负数的性质等知识点逐项排查即可．
【详解】解：A．因为勾股数都是整数，所以不是一组勾股数，则A选项是假命题，不符合题意；
B．两直线平行，同旁内角互补，则B选项是假命题，不符合题意；
C．在一次函数y= -3x+2中，因为k=-3<0，所以y随x的增大而减小，则C选项是假命题，不符合题意；
D．由，则有x-2=0，y+5=0，即x=2，y=-5，所以y+x=-3正确，则D选项是真命题，符合题意．
故选：D．
【点睛】此题考查了命题的真假、勾股数的定义、平行线的性质、一次函数的性质以及非负数的性质等知识点，解题的关键是灵活运用相关性质．
6. 下列所描述的四个变化过程中，变量之间的关系不能看成函数关系的是（ ）
A. 三角形的一个外角度数度和与它相邻的内角度数度的关系
B. 树的高度为厘米，每个月长高厘米，月后树的高度为厘米，与的关系
C. 正方形的面积（平方厘米）和它的边长（厘米）的关系
D. 一个正数的平方根是，随着这个数的变化而变化，与之间的关系
【答案】D
【解析】
【分析】根据题目的已知找出等量关系，列出与的关系式即可判断．
【详解】解：，对于的每一个值，都有唯一的值与它对应，故A不符合题意；
B．，对于的每一个值，都有唯一的值与它对应，故B不符合题意；
C．，对于的每一个值，都有唯一的值与它对应，故C不符合题意；
D．，对于的每一个值，都有两个的值与它对应，故D符合题意；
故选：．
【点睛】本题考查了函数的概念，根据题目的已知列出与的关系式是解题的关键．
7. 如图，一次函数y＝x的图象与y＝kx＋7的图象相交于点A，则方程组的解是（ ）
A. B. C. D.
【答案】A
【解析】
【分析】先求交点的坐标，然后根据两条直线的交点坐标即可写出方程组的解．
【详解】解：把x=2代入y=x得y=3，
所以交点坐标为（2，3），
所以方程组的解是．
故选：A．
【点睛】本题考查了一次函数与二元一次方程（组）：方程组的解就是两个相应的一次函数图象的交点坐标．
8. 学校学生会招募新会员，小林同学的心理测试、笔试、面试得分分别为80分、90分、70分，若依次按照3：2：5的比例确定成绩，则小林同学的最终成绩为（ ）
A. 80B. 82C. 77D. 78
【答案】C
【解析】
【分析】由加权平均数的含义列式列式计算即可．
【详解】解：由题意得（分），
所以小林同学的最终成绩为77分．
故选C．
【点睛】本题主要考查的是加权平均数的含义及计算，掌握加权平均数的含义是解题的关键．
9. 如图，矩形的两边、分别在轴、轴上，点与原点重合，点A（-2，3），将矩形ABCD沿轴向右翻滚，经过一次翻滚点A对应点记为，经过第二次翻滚点A对应点记为依此类推，经过3次翻滚后点A对应点的坐标为（ ）
A. （8，2）B. （3，2）C. （3，3）D. （5，0）
【答案】D
【解析】
【分析】根据A点坐标可知长方形的长和宽，根据长方形的长和宽分析每次翻滚后A点的落点，由此可解决本题．
【详解】解：∵A点坐标为（-2，3），
∴AB=DC=3，AD=BC=2，
第一次翻滚后点坐标为：（3，2），
第二次翻滚后点的坐标为（5，0），
第三次翻滚是以点为中心进行翻滚，故（5，0），
故选：D．
【点睛】本题考查平面直角坐标系中的点，能够根据题意分析出图形的运动过程是解决本题的关键．
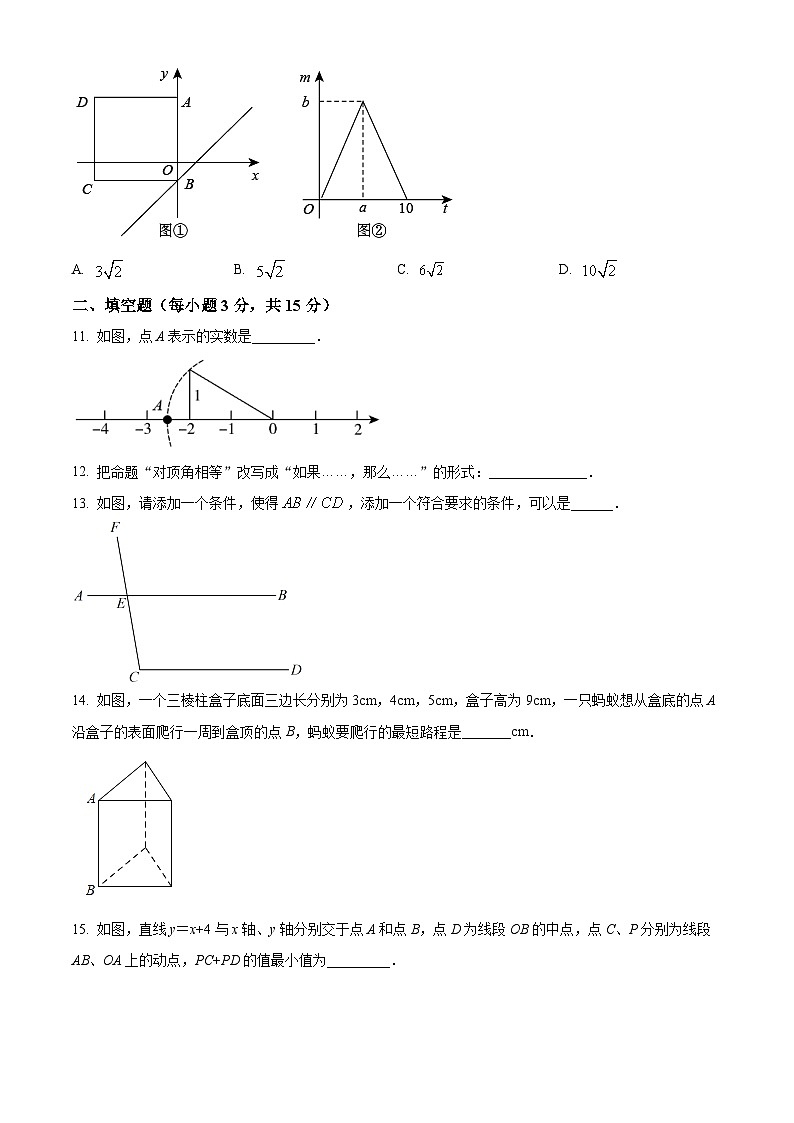
10. 如图①，正方形ABCD在直角坐标系中，其中AB边在y轴上，其余各边均与坐标轴平行，直线l：y=x-1沿y轴的正方向以每秒1个单位的速度平移，在平移的过程中，该直线被正方形ABCD的边所截得的线段长为m（米），平移的时间为t（秒），m与t的函数图象如图②所示，则图②中b的值为（ ）
A. B. C. D.
【答案】B
【解析】
【分析】连接AC，根据直线与坐标轴的交点得出直线与AC平行，因此当直线向上平移到A点时被正方形ABCD的边所截得的线段长最大b=AC，由图②可知此时a=5，由速度求出AB的长再根据勾股定理即可解答；
【详解】解：如图连接AC，
由y=x-1可得，当x=0时，y=-1，当y=0时，x=1，
∴直线与坐标轴构成的三角形是等腰直角三角形，
∴直线与x轴的夹角是45°，
∵正方形ABCD中，AD∥BC∥x轴，∠ACB=45°，
∴直线l与AC平行，
∴当直线向上平移到A点时被正方形ABCD的边所截得的线段长最大b=AC，
由图②可知，当a=5时，直线平移到A点，
∴AB=1×5=5米
∴b=AC=米，
故选： B．
【点睛】本题考查了一次函数的平移，等腰三角形的判定和性质，正方形的性质，勾股定理，根据题意弄懂图象所表达的含义是解题关键．
二、填空题（每小题3分，共15分）
11. 如图，点A表示的实数是_________．
【答案】
【解析】
【分析】根据勾股定理可得OB的长，再求出OA的长，然后求得点A所表示的数即可．
【详解】解：如图：由题意得：OB=，
∵OA=OB
∴点A表示的实数是
故答案为：．
【点睛】本题主要考查了数轴、勾股定理等知识点，解答本题的关键是求得OA的长度．
12. 把命题“对顶角相等”改写成“如果……，那么……”的形式：______________．
【答案】两个角是对顶角，那么这两个角相等
【解析】
【分析】先找到命题的题设和结论，再写成“如果…，那么…”的形式．
【详解】解：把命题“对顶角相等”改写成“如果……，那么……”的形式为：
如果两个角是对顶角，那么这两个角相等．
故答案为：两个角是对顶角，那么这两个角相等
【点睛】本题主要考查了将原命题写成条件与结论的形式，“如果”后面是命题的条件，“那么”后面是条件的结论，解决本题的关键是找到相应的条件和结论，比较简单．
13. 如图，请添加一个条件，使得，添加一个符合要求的条件，可以是______．
【答案】∠BEF=∠C或∠AEC=∠C或∠BEC+∠C=180°（答案不唯一）．
【解析】
【分析】欲证AB∥CD，在图中发现AB、CD被直线FC所截，根据平行线的判定方法得出答案即可．
【详解】添加的条件可以是∠BEF=∠C或∠AEC=∠C或∠BEC+∠C=180°．
∵∠BEF=∠C，
∴AB∥CD（同位角相等，两直线平行）．
∵∠AEC=∠C，
∴AB∥CD（内错角相等，两直线平行）．
∵∠BEC+∠C=180°，
∴AB∥CD（同旁内角互补，两直线平行）．
故答案为：∠BEF=∠C或∠AEC=∠C或∠BEC+∠C=180°（答案不唯一）．
【点睛】此题考查平行线的判定，解答此类要判定两直线平行的题，可围绕截线找同位角、内错角或同旁内角．本题是一道探索性条件开放性题目，能有效地培养“执果索因”的思维方式与能力．
14. 如图，一个三棱柱盒子底面三边长分别为3cm，4cm，5cm，盒子高为9cm，一只蚂蚁想从盒底的点A沿盒子的表面爬行一周到盒顶的点B，蚂蚁要爬行的最短路程是_______cm．
【答案】15
【解析】
【分析】将三棱柱侧面展开得出矩形，求出矩形对角线的长度即可．
【详解】解：如图，右侧为三棱柱的侧面展开图，AA′＝3+4+5＝12cm，A′B＝9cm，∠AA′B＝90°，
∴AB＝ ＝15cm，
故答案为：15．
【点睛】本题考查了三棱柱的侧面展开图，两点之间线段最短，勾股定理，画出三棱柱的侧面展开图，运用勾股定理是解题关键．
15. 如图，直线y＝x+4与x轴、y轴分别交于点A和点B，点D为线段OB的中点，点C、P分别为线段AB、OA上的动点，PC+PD的值最小值为_________．
【答案】
【解析】
【分析】先作点D关于x轴的对称点，过点作C⊥AB垂足为C，线段C交x轴于点P,此时可知P=PD，即可求得B的长以及PC+PD= PC+P=C，然后再说明△CB是等腰直角三角形并用勾股定理求出C长度即可.
【详解】解：作点D关于x轴的对称点，过点作C⊥AB垂足为C，线段C交x轴于点P，连接PD，由轴对称的基本性质，可知P=PD，
∴PC+PD= PC+P=C，此时直线外一点到已知线段垂线段最短，此时PC+PD值最小．
令一次函数y=x+4中x=0，则y=4，
∴点B坐标为（0，4）；
∵D（0,2），
∴O=OD=2,
∴ B=OB+ O=4+2=6
令y=x+4中y=0，则x+4=0，解得：x=-4，
∴点A的坐标为（-4，0）．
∴OA=OB
∴∠CB=45°
又∵C⊥AB垂直为C
∴∠OP=45°
∴△CB是等腰直角三角形
设C=x，则BC=x
由勾股定理可得：,即，解得x=
∴PC+PD的最小值为．
故答案为．
【点睛】本题主要考查了轴对称性质、直线外一点到已知直线上所有点的连线中垂线段最短、勾股定理知识点,熟练掌握知识是解答本题的关键．
三、解答题（共7小题，满分75分）
16. 计算
【答案】
【解析】
【分析】先化简二次根式，绝对值，以及计算﹣1的零指数幂，再乘除，再加减．
【详解】解：原式
．
【点睛】本题考查化简二次根式，二次根数的混合运算，零指数幂，绝对值，能够掌握运算顺序是解决本题的关键．
17. 某学校要调查学生关于“新冠肺炎”防治知识的了解情况，从七、八年级各随机抽取了10名学生进行测试（满分10分），测试成绩整理、描述和分析如下：（成绩得分用x表示，共分成四组：A．8.0≤x＜8.5，B．8.5≤x＜9.0，C．9.0≤x＜9.5，D．9.5≤x≤10.0）
七年级10名学生的成绩是：8.0，8.6，9.9，9.6，9.0，9.9，10.0，8.2，8.9，9.9．
八年级10名学生的成绩在C组中的数据是：9.4，9.0，9.3．
七、八年级抽取的学生成绩统计图表如下：
根据以上信息，解答下列问题：
（1）请直接写出上述图表中a，b，c的值；
（2）根据以上数据，你认为该校七、八年级中哪个年级学生掌握“新冠肺炎”知识较好？请说明理由．
（3）该校七、八年级共1200人参加了此次调查活动，估计参加此次调查活动成绩优秀（x≥9.0）的学生人数是多少．
【答案】（1）a=40，b=9.35，c=9.9；
（2）八年级，理由见解析；
（3）780人．
【解析】
【分析】（1）由八年级学生成绩的扇形统计图可求得得分在C组的百分比，根据各百分比的和为1即可求得a的值；由扇形统计图可求得八年级得分在各个组的人数，从而可求得中位数b；根据七年级10名学生成绩中出现次数最多的是众数，则可得c；
（2）两个年级得分的平均数相同，但八年级得分的方差较小，根据方差的特征即可判断八年级学生掌握得更好；
（3）求出两个年级得分的优秀率作为全校得分的优秀率，即可求得得分为优秀的学生人数．
【小问1详解】
解：由八年级学生成绩的扇形统计图，成绩在C组的学生所占的百分比为：30%，
∴a%=1-10%-20%-310×100%=40%，
∴a=40，
八年级得分在A组的有：10×20%=2（人），得分在B组的有：10×10%=1（人），得分在D组的有：10×40%=4（人），
由此可知，得分的中位数为：b=（9.3+9.4）÷2=9.35，
七年级10名学生的成绩中9.9分出现的次数最多，即众数为9.9，故c=9.9．
【小问2详解】
解：八年级学生掌握得更好，
理由如下：因为两个年级的平均数相同，而八年级的众数与中位数都比七年级的高，说明八年级高分的学生更多；八年级成绩的方差比七年级的方差小，说明八年级成绩的波动更小，成绩更稳定．
【小问3详解】
解：两个年级得分的优秀率为：（6+7）÷20×100%=65%，
1200×65%=780（人），
所以参加此次调查活动成绩优秀的学生人数约为780人．
【点睛】本题是统计图与统计表的综合，考查了扇形统计图，方差、中位数、众数，样本估计总体等知识，读懂统计图，从中获取信息是关键．
18. 小明说，在匀速运动过程中，t每增加1，vt增加了v，因此s也增加了v．而如图所示的匀速运动图像中，t从1变成2时，函数值从2变为4，增加了2，因此该一次函数中v的值是2．
（1）用小明的这种方法，若已知一次函数的图像经过（0，2）、（1，3）两点，尝试确定这个一次函数的表达式，请你将过程补充完整．
设一次函数的表达式为，
∵一次函数的图像经过（0，2）、（1，3）两点，
∴b= ．
∵x从0变成1时，增加了1，函数值从2变为3，增加了1，
∴________．
∴该一次函数的表达式为________．
（2）尝试用待定系数法确定这个一次函数表达式：
设一次函数的表达式为，
∵一次函数的图像经过（0，2）、（1，3）两点，
把（0，2）、（1，3）代入得_______________________，
解得________．
∴该一次函数的表达式为_________．
【答案】（1）2，1，
（2），，
【解析】
【分析】（1）运用待定系数法求函数解析式即可即可；
（1）运用待定系数法求函数解析式即可即可．
【小问1详解】
解：设一次函数的表达式为，
∵一次函数的图像经过（0，2）、（1，3）两点，
∴，解得．
∵x从0变成1时，增加了1，函数值从2变为3，增加了1，
∴1．
∴该一次函数的表达式为．
故答案为2，1，．
【小问2详解】
解：设一次函数表达式为，
∵一次函数的图像经过（0，2）、（1，3）两点，
把（0，2）、（1，3）代入得，．
解得．
∴该一次函数的表达式为．
故答案为，，．
【点睛】本题主要考查了运用待定系数法法求一次函数解析式，掌握待定系数法的使用方法是解答本题的关键．
19. 在一次“寻宝”游戏中，寻宝人已经找到了A（-2，3）和B（2，3）两个标志点，并且知道藏宝地点坐标为（-1，-1）．请在下图中建立平面直角坐标系并确定宝藏的位置．
【答案】见解析
【解析】
【分析】先根据A、B的坐标建立平面直角坐标系，然后确定宝藏的位置即可．
【详解】解：宝藏的位置如图：
．
【点睛】本题主要考查了坐标确定位置，正确得出原点位置是解答本题的关键．
20. 如图，在△ABC中，AB=4，AC=3，DE是BC的垂直平分线，交BC于点D，交AB于点E，AF⊥BC于点F．关于△ABC的形状，小明和小亮展开以下讨论：
小明：如果△ABC是直角三角形，那么我可以求出AE的长．
我的思路是这样的：如图，连接CE，设AE=x，则BE=4-x，因为DE是BC的垂直平分线，所以CE=BE=4-x…
小亮：如果DF的长为，此时△ABC是直角三角形．
（1）请补充完整小明的求解过程；
（2）请判断小亮的说法是否正确?并说明理由．
【答案】（1）补充见解析
（2）正确，理由见解析
【解析】
【分析】（1）连接CE，设AE＝x，根据线段垂直平分线的性质得出CE＝BE＝4−x，利用勾股定理列出关于x的方程，求出x的值即可；
（2）设BD＝y，则CD＝y，用y表示出BF和CF，利用勾股定理列出y方程，求出y的值，进而利用勾股定理的逆定理证明△ABC是直角三角形．
【小问1详解】
解：补充如下：
∠BAC=90°，AC=3，AB=4，
，即，解得，
；
【小问2详解】
解：小华的说法正确．
理由如下：设BD=y，则CD=y，
，
，
AF⊥BC，
，即，解得，
，
在中，，可得为直角三角形．
【点睛】本题考查勾股定理以及勾股定理逆定理的应用，解题的关键是掌握线段垂直平分线的性质．
21. 一方有难，八方支援．郑州暴雨牵动数万人的心，众多企业也伸出援助之手．某公司购买了一批救灾物资并安排两种货车运往郑州．调查得知，2辆小货车与3辆大货车一次可以满载运输1800件；3辆小货车与4辆大货车一次可以满载运输2500件．
（1）求1辆大货车和1辆小货车一次可以分别满载运输多少件物资？
（2）现有3100件物资需要再次运往郑州，准备同时租用这两种货车，每辆均全部装满货物，问有哪几种租车方案?
（3）在（2）的条件下，若1辆小货车需租金400元/次，1辆大货车需租金500元/次．请选出费用最少的租车方案，并求出最少的租车费用．
【答案】（1）1辆小货车一次满载运输300件物资，1辆大货车一次满载运输400件物资
（2）共有3种租车方案，方案1：租用9辆小货车，1辆大货车；方案2：租用5辆小货车，4辆大货车；方案3：租用1辆小货车，7辆大货车
（3）租用1辆小货车，7辆大货车，最少租车费为3900元
【解析】
【分析】（1）设1辆小货车一次满载运输x件物资，1辆大货车一次满载运输y件物资，然后根据题意列二元一次方程组求解即可；
（2）根据题意可得300a+400b=3100，再用b表示出a，然后根据a、b均为整数进行列举即可解答；
（3）将小货车和大货车每次的租金代入300a+400b里计算，然后比较即可．
【小问1详解】
解：设1辆小货车一次满载运输x件物资，1辆大货车一次满载运输y件物资，
依题意得： 解得：
答：1辆小货车一次满载运输300件物资，1辆大货车一次满载运输400件物资．
【小问2详解】
接：设租用小货车a辆，大货车b辆，
依题意得：300a+400b=3100，
∴．
又∵a，b均为非负整数，
∴或 或，
∴共有3种租车方案，
方案1：租用9辆小货车，1辆大货车；
方案2：租用5辆小货车，4辆大货车；
方案3：租用1辆小货车，7辆大货车．
【小问3详解】
解：方案1所需租车费为400×9+500×1=4100（元）；
方案2所需租车费为400×5+500×4=4000（元）；
方案3所需租车费为400×1+500×7=3900（元）．
∴费用最少的租车方案为：租用1辆小货车，7辆大货车，最少租车费为3900元．
【点睛】本题主要考查了二元一次方程组的应用、二元一次方程的应用以及代数式求值等知识点，认真审题、明确题意、弄清量与量之间的关系是解答本题的关键．
22. 小王骑自行车从A地出发前往B地，同时小李步行从B地出发前往A地，如图的折线OPQ和线段EF，分别表示小王、小李两人与A地的距离y甲、y乙与他们所行时间x（h）之间的函数关系，且OP与EF相交于点M．
（1）求线段OP对应y甲与x的函数关系式（不必注明自变量x的取值范围）；
（2）求y乙与x的函数关系式以及A，B两地之间的距离；
（3）直接写出经过多少小时，甲、乙两人相距3km．
【答案】（1）y甲=18x
（2）y乙=﹣6x+12，12km
（3）小时或小时
【解析】
【分析】（1）设线段OP对应的函数解析式为y甲=k1x，由图象可知9=0.5k，得k1=18，由此可知线段OP对应的函数解析式；
（2）设与x的函数关系式是y乙=k2x+n，有图象可知代入（0.5,9）（2,0）两点后求出解析式，当时间为0时，小李与A地的距离为A，B两地的距离；
（3）先计算出小李与小王的速度，根据相遇前相距3km，与相遇后相距3km两种情况分别分类计算即可．
【小问1详解】
解：设线段OP对应的函数解析式为y甲=k1x，
∴9=0.5k，解得k1=18，
∴线段OP对应函数解析式为y甲=18x；
【小问2详解】
解：∵经过点（0.5，9），（2，0）
设y乙与x的函数关系式是y乙=k2x+n，
∴，解得，
即y乙与x的函数关系式是y乙=﹣6x+12，
当x=0时，y乙=12，
∴A、B两地的距离是12km；
【小问3详解】
解：
，
相遇前相距3km：，
相遇后相距3km：
经过小时或小时时，甲、乙两人相距3km．
【点睛】本题考查利用一次函数解决实际问题，求一次函数的解析式，行程问题，能够掌握数形结合思想是解决本题的关键．
23. —副三角板如图1摆放，，，，点F在BC上，点A在DF上，且AF平分，现将三角板DFE绕点F顺时针旋转（当点D落在射线FB上时停止旋转）．
（1）当________时，；当________时，；
（2）在旋转过程中，DF与AB的交点记为P，如图2，若有两个内角相等，求的度数；
（3）当边DE与边AB、BC分别交于点M、N时，如图3，若，比较与的大小，并说明理由．
【答案】（1）30，60；（2）∠APD的度数为60°或105°或150°；（3）=，理由见解析．
【解析】
【分析】（1）当∠AFD=30°时，AC//DF，依据角平分线的定义可得∠CAF=∠FAB=30°，然后根据平行线的判定定理可证AC//DF；当∠AFD=60°时，DF⊥AB，根据三角形的内角和定理即可证明；
（2）分为∠FAP=∠AFP，∠AFP=∠APF，∠APF=∠FAP三种情况求解即可;
（3）先依据证明∠FNM=30°+∠BMN，然后根据三角形外角的性质以及∠AFM和∠BMN的关系可证∠FMN=30°+∠BMN，最后运用等量代换即可说明．
【详解】解：（1）如图1所示：
当∠AFD=30°时，AC//DF理由如下：
∵∠CAB=60°，AF平分∠CAB
∴∠CAF=30"
∵∠AFD=30°
∴∠CAF=∠AFD
∴AC//DF；
如图2所示：当∠AFD=60°时，DF⊥AB
理由如下：
∵∠CAB=60°，AF平分∠CAB
∴∠FAG=30°
∵∠AFD=60°
∴∠FGA=180°-∠AFD -∠FAG =90°
∴DF⊥AB；
故答案为：30，60．
（2）∵∠CAB=60°，AF平分∠FAG CAB.
∴∠FAP=30°
当图3所示：
当∠FAF=∠AFP=30°时，∠APD=∠FAP+∠AFP=30°+30°=60°；
如图4所示：
当∠AFP=∠APF时.
∵∠FAP=30°，∠AFP=∠APF
∴∠AFP=∠APF=（180°-30°）=75°
∴∠APD=∠FAP+ ∠AFP=30°+75°=105°；
如图5所示：
当∠APF=∠FAP=30°时.
∠APD=180°-30°=150°
综上所述，∠APD的度数为60°或105°或150°；
（3）∠FMN=∠FNM，理由如下：
如图6所示：
∵∠FNM是△BMN的一个外角
∴∠FNM=∠B+∠BMN
∵∠B=30°
∴∠FNM=∠B+∠BMN=30°+∠BMN
∵∠BMF是△AFM的一个外角
∴∠BMF=∠MAF+∠AFM，即∠BMN+ ∠FMN=∠MAF+∠AFM
又∵∠MAF=30°，∠AFM=2∠BMN
∴∠BMN+∠FMN=30°+2∠BMN
∴∠FMN=30°+∠BMN
∴∠FNM=∠FMN．
【点睛】本题主要考查了角平分线的定义、三角形的内角和定理、平行线的判定定理、角形的外角的性质等知识点，掌握并灵活应用相关知识是解答本题的关键．年级
七年级
八年级
平均数
9.2
9.2
中位数
9.3
b
众数
c
10.0
方差
0.52
0.504