

新高考物理一轮复习讲义第1章 运动的描述 专题强化一 运动图像 追及相遇问题 (含解析)
展开考点一 x-t图像和v-t图像的理解与应用
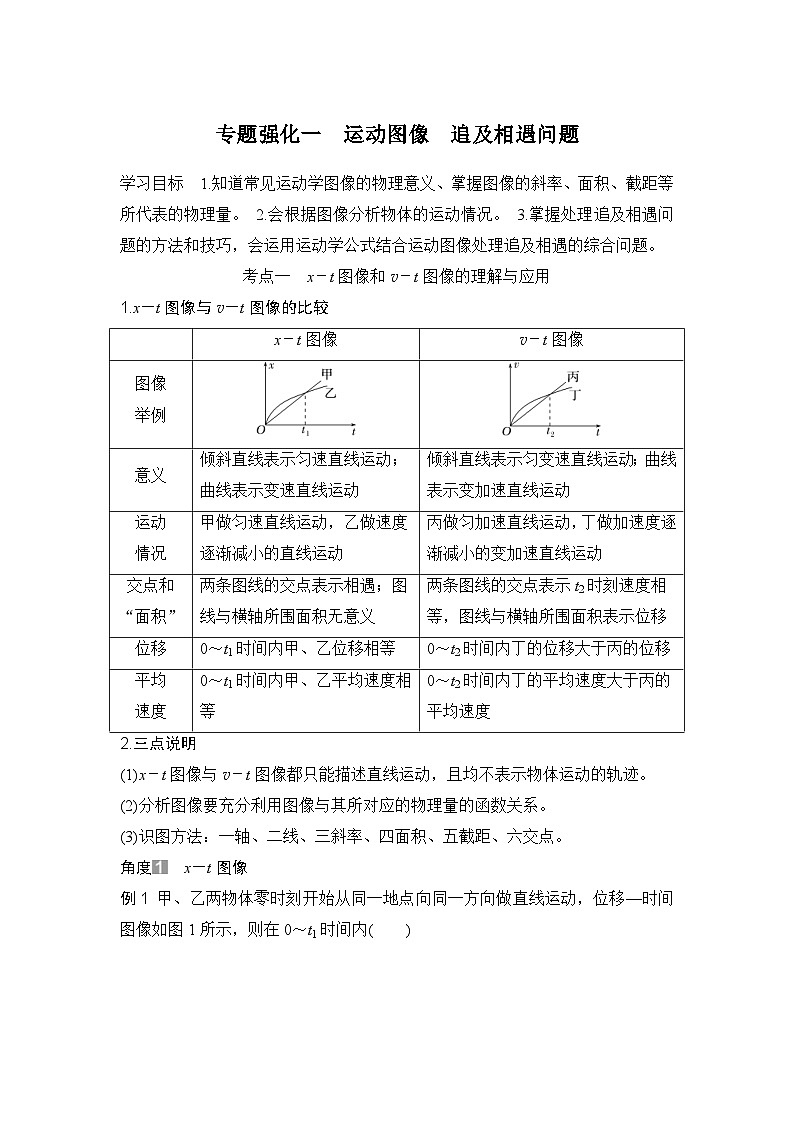
1.x-t图像与v-t图像的比较
2.三点说明
(1)x-t图像与v-t图像都只能描述直线运动,且均不表示物体运动的轨迹。
(2)分析图像要充分利用图像与其所对应的物理量的函数关系。
(3)识图方法:一轴、二线、三斜率、四面积、五截距、六交点。
角度 x-t图像
例1 甲、乙两物体零时刻开始从同一地点向同一方向做直线运动,位移—时间图像如图1所示,则在0~t1时间内( )
图1
A.甲的速度总比乙大
B.甲、乙位移相同
C.甲经过路程比乙小
D.甲、乙均做加速运动
答案 B
解析 位移—时间图像中,图线斜率大小等于物体速度大小。由题图可知,甲做匀速直线运动,乙做变速直线运动,D错误;靠近t1时刻时乙的斜率大于甲的斜率,即乙的速度大于甲的速度,故A错误;在0~t1时间段内,甲、乙物体的初位置和末位置相同,故位移相同,B正确;甲、乙物体做的是单向直线运动,两者的位移大小相等,路程也相同,故C错误。
跟踪训练
1.(多选)a、b两质点在同一直线上运动,它们运动的位移x随时间t变化的关系如图2所示,其中a质点的x-t图像为抛物线的一部分,第7 s末图像处于最高点,b质点的图像为直线。下列说法正确的是( )
图2
A.a质点的初速度大小为7 m/s
B.a质点的加速度大小为2 m/s2
C.a质点减速过程通过的位移大小为50 m
D.两质点相遇时,b质点的速度小于a质点的速度
答案 BD
解析 a质点的x-t图像为抛物线的一部分,说明a质点做匀减速直线运动,7 s末速度为零,则有v0+at7=0,0~10 s内,a质点的位移为x=40 m,则有x=v0t10+eq \f(1,2)ateq \\al(2,10),联立解得v0=14 m/s,a=-2 m/s2,所以a质点的初速度大小为
14 m/s,加速度大小为2 m/s2,故A错误,B正确;a质点在0~7 s内做匀减速运动,通过的位移为x=v0t7+eq \f(1,2)ateq \\al(2,7)=49 m,故C错误;根据x-t图像的斜率表示速度,知10 s末两质点相遇时,a质点的速度较大,故D正确。
角度 v-t图像
例2 (多选)甲、乙两个物体从同一地点、沿同一直线同时做直线运动,其v-t图像如图3所示,则( )
图3
A.2 s时甲和乙相遇
B.2 s时甲的速度方向开始反向
C.2~6 s内甲相对乙做匀速直线运动
D.乙在2~4 s内的加速度和它在4~6 s内的加速度大小相等,方向相反
答案 AC
解析 由题图可知,0~2 s内,甲、乙两图线与坐标轴围成的面积相等,即两者通过的位移相等,甲、乙两个物体又是从同一地点沿同一方向开始运动的,所以2 s时甲、乙相遇,故A正确;甲物体的速度一直沿正方向,速度方向没有改变,故B错误;2~6 s内,甲与乙速度之差是定值,说明甲相对乙做匀速直线运动,故C正确;根据斜率表示加速度可知,2~6 s内,乙的加速度一定,在4 s时加速度方向没有反向,改变的是速度方向,故D错误。
跟踪训练
2.(2022·河北卷,1) 科学训练可以提升运动成绩,某短跑运动员科学训练前后百米全程测试中,速度v与时间t的关系图像如图4所示。由图像可知( )
图4
A.0~t1时间内,训练后运动员的平均加速度大
B.0~t2时间内,训练前、后运动员跑过的距离相等
C.t2~t3时间内,训练后运动员的平均速度小
D.t3时刻后,运动员训练前做减速运动,训练后做加速运动
答案 D
解析 根据v-t图像的斜率表示加速度,由题图可知0~t1时间内,训练后运动员的平均加速度比训练前的小,故A错误;根据v-t图像与横轴围成的面积表示位移,由题图可知0~t2时间内,训练前运动员跑过的距离比训练后的大,故B错误;根据v-t图像与横轴围成的面积表示位移,由题图可知t2~t3时间内,训练后运动员的位移比训练前的位移大,根据平均速度等于位移与时间的比值,可知训练后运动员的平均速度大,故C错误;由v-t图像可直接看出,t3时刻后,运动员训练前速度减小,做减速运动,运动员训练后速度增加,做加速运动,故D正确。
考点二 “数学思维”分析非常规图像问题
1.三类图像
(1)a-t图像
由v=v0+at可知图像与横轴所围面积表示速度变化量Δv,如图5甲所示。
(2)eq \f(x,t)-t图像
由x=v0t+eq \f(1,2)at2可得eq \f(x,t)=v0+eq \f(1,2)at,图像的斜率为eq \f(1,2)a,如图乙所示。
(3)v2-x图像
由v2-veq \\al(2,0)=2ax可知v2=veq \\al(2,0)+2ax,图像斜率为2a,如图丙所示。
图5
2.解题技巧
(1)用函数思想分析图像
对于非常规运动图像,可由运动学公式推导出两个物理量间的函数关系,来分析图像的斜率、截距、面积的含义。
(2)要注意应用解析法和排除法,两者结合提高选择题图像类题型的解题准确率和速度。
例3 一质点沿直线运动,如图6所示是从t=0时刻开始的质点的eq \f(x,t)-t图像(x为位移),可以推知( )
图6
A.质点做匀减速运动
B.加速度的大小是1 m/s2
C.t=2 s时的速度是1 m/s
D.t=2 s时位移是3 m
答案 B
解析 由题意可得图线的函数表达式为eq \f(x,t)=1+eq \f(1,2)t,即x=t+eq \f(1,2)t2,又因为匀变速直线运动中位移公式为x=v0t+eq \f(1,2)at2,根据对应关系得v0=1 m/s,a=1 m/s2>0,因此质点做匀加速运动,故A项错误,B项正确;当t=2 s时,根据公式v=
v0+at,代入数据得v2=3 m/s,故C项错误;当t=2 s时,代入表达式x=t+eq \f(1,2)t2,可得位移x2=4 m,故D项错误。
跟踪训练
3.一物体由静止开始,在粗糙的水平面内沿直线运动,其加速度a随时间t变化的a-t图像如图7所示。若选物体开始运动的方向为正方向,那么,下列说法中正确的是( )
图7
A.在0~2 s的时间内,物体先做匀速直线运动后做匀减速运动
B.在2 s时物体的位移最大
C.在2~3 s的时间内,物体速度的变化量为-1 m/s
D.在0~4 s的时间内,物体的位移为零
答案 C
解析 0~1 s内,加速度不变,物体做匀加速运动,1~2 s内,加速度数值减小,物体做加速度减小的变加速运动,A错误;2 s时,加速度为0,速度最大,B错误;a-t图像中图线与横轴所围的面积表示速度的变化量,2~3 s的时间内,速度变化量为Δv=eq \f(1,2)×1×(-2)m/s=-1 m/s,C正确;0~4 s内,物体的速度变化量为0,即物体在4 s时停止运动,位移不为0,D错误。
4.(多选)为检测某新能源动力车的刹车性能,一次在平直公路上实验时,动力车整个刹车过程中位移与速度平方之间的关系图像如图8所示,下列说法正确的是( )
图8
A.动力车的初速度为20 m/s
B.刹车过程动力车的加速度大小为5 m/s2
C.刹车过程持续的时间为10 s
D.刹车过程经过6 s时动力车的位移为30 m
答案 AB
解析 根据0-v2=-2ax得,eq \f(x,v2)=eq \f(1,2a),可知eq \f(1,2a)=eq \f(40,400),解得刹车过程中加速度大小a=5 m/s2,由图线可知veq \\al(2,0)=400(m/s)2,则动力车的初速度v0=20 m/s,选项A、B正确;刹车过程持续的时间t=eq \f(v0,a)=eq \f(20,5) s=4 s,选项C错误;刹车过程中6 s内的位移等于4 s内的位移,则x=eq \f(veq \\al(2,0),2a)=eq \f(400,10) m=40 m,选项D错误。
考点三 追及相遇问题
1.解答追及和相遇问题的三种方法
2.情境分析法的基本思路
3.特别提醒
若被追赶的物体做匀减速直线运动,一定要注意判断被追上前该物体是否已经停止运动。
角度 图像法在追及相遇中的应用
例4 甲、乙两汽车在一平直公路上同向行驶,它们的v-t图像如图9所示,t=1 s时,甲、乙第一次并排行驶,则( )
图9
A.t=0时,甲在乙的前面4.5 m处
B.t=2 s时,甲在乙的前面6 m处
C.两次并排行驶的时间间隔为2.5 s
D.两次并排行驶的位置间距为8 m
答案 D
解析 根据两汽车的v-t图像可得瞬时速度的表达式分别为v甲=(8-2t) m/s,
v乙=(2+t) m/s,t=1 s时,甲、乙第一次并排行驶,即两车此时相遇,在第1 s内甲和乙的位移之差为Δx=(eq \f(8+6,2)×1-eq \f(2+3,2)×1) m=4.5 m,因甲比乙的速度大,则属于甲追乙,则t=0时,甲在乙的后面4.5 m处,故A错误;在t=2 s时,两车的距离为Δx2=(eq \f(6+4,2)×1-eq \f(3+4,2)×1) m=1.5 m,甲在乙的前面1.5 m处,故B错误;t=2 s时两者的速度相等,根据图像的对称性可知t=1 s和t=3 s两车两次相遇,故两次并排行驶的时间间隔为2 s,故C错误;t=1~3 s两车的位移相同,大小为x=eq \f(6+2,2)×2 m=8 m,故D正确。
角度 追及和相遇问题
例5 (2023·广东汕头质检)某一长直的赛道上,一辆F1赛车前方200 m处有一安全车正以10 m/s的速度匀速前进,这时赛车从静止出发以2 m/s2的加速度追赶。
(1)求赛车出发3 s末的瞬时速度大小;
(2)求赛车追上安全车所需的时间及追上之前与安全车的最远距离;
(3)当赛车刚追上安全车时,赛车手立即刹车,使赛车以4 m/s2的加速度做匀减速直线运动,则两车再经过多长时间第二次相遇?(设赛车可以从安全车旁经过而不相碰)
答案 (1)6 m/s (2)20 s 225 m (3)20 s
解析 (1)赛车3 s末的速度
v1=a1t1=2×3 m/s=6 m/s。
(2)设经t2时间追上安全车,由位移关系得
v0t2+200 m=eq \f(1,2)a1teq \\al(2,2)
解得t2=20 s
此时赛车的速度v=a1t2=2×20 m/s=40 m/s
当两车速度相等时,两车相距最远
由v0=a1t3得两车速度相等时,经过的时间
t3=eq \f(v0,a1)=eq \f(10,2) s=5 s
两车最远相距Δs=v0t3+200 m-eq \f(1,2)a1teq \\al(2,3)
=eq \b\lc\(\rc\)(\a\vs4\al\c1(10×5+200-\f(1,2)×2×52))m=225 m。
(3)假设再经t4时间两车第二次相遇(两车一直在运动)
由位移关系得vt4-eq \f(1,2)a2teq \\al(2,4)=v0t4
解得t4=15 s
赛车停下来的时间t′=eq \f(v,a2)=eq \f(40,4) s=10 s
所以t4=15 s不符合实际,两车第二次相遇时赛车已停止运动
设再经时间t5两车第二次相遇,应满足eq \f(v2,2a2)=v0t5
解得t5=20 s。
跟踪训练
5.(多选)两辆汽车在同一直道上以相等的速度v0做同向直线运动,某时刻前车突然熄火做加速度大小为a1的匀减速运动,后车司机经Δt时间后刹车,以大小为a2的加速度做匀减速运动,结果两车同时停下且没有发生碰撞,则在前车熄火前,两车正常行驶时之间距离至少是( )
A.eq \f(v0Δt,2) B.v0Δt
C.eq \f(veq \\al(2,0),2)eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,a1)+\f(1,a2))) D.eq \f(veq \\al(2,0),2)eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,a1)-\f(1,a2)))
答案 AD
解析 前车减速到零所需时间为t1=eq \f(v0,a1),减速通过的位移为x1=eq \f(veq \\al(2,0),2a1),后车在Δt时间内通过的位移为x′=v0Δt,后车减速到零经历的时间为t2=eq \f(v0,a2),减速通过的位移为x2=eq \f(veq \\al(2,0),2a2),由于两车同时停下且没有发生碰撞,故t1-Δt=t2,x′+x2=x1+s0,联立解得,在前车熄火前,两车正常行驶时之间距离至少是s0=eq \f(v0Δt,2)或eq \f(veq \\al(2,0),2)eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,a1)-\f(1,a2))),故A、D正确,B、C错误。
6.(多选)(2023·湖北九校联考)假设高速公路上甲、乙两车在同一平直车道上同向行驶。甲车在前,乙车在后,速度大小均为v0=30 m/s,两车间距离为s0=100 m。t=0时刻甲车遇紧急情况后,甲、乙两车的加速度随时间变化关系分别如图10(a)、(b)所示。取原运动方向为正方向。下列说法正确的是( )
图10
A.t=3 s时两车相距最近
B.t=6 s时两车间距离最近,为10 m
C.0~9 s内两车位移大小之差为45 m
D.两车在0~9 s内不会相撞
答案 BCD
解析 由加速度—时间图像可画出两车的速度—时间图像,如图所示。
由图像可知,t=6 s时两车共速,此时两车间的距离最近,图中阴影部分面积表示0~6 s内两车位移大小之差,即Δx′=eq \f(1,2)×30×3 m+eq \f(1,2)×30×(6-3)m=90 m<100 m,则t=6 s时两车相距最近为Δs=s0-Δx′=10 m,所以两车不会相撞,选项B、D正确,A错误;0~9 s内两车位移大小之差为Δx″=eq \f(1,2)×30×3 m=45 m,选项C正确。
A级 基础对点练
对点练1 x-t图像和v-t图像的理解与应用
1.A、B两物体沿同一直线运动,运动过程中的x-t图像如图1所示,下列说法正确的是( )
图1
A.4 s时A物体运动方向发生改变
B.0~6 s内B物体的速度逐渐减小
C.0~5 s内两物体的平均速度相等
D.0~6 s内某时刻两物体的速度大小相等
答案 D
解析 x-t图像的斜率表示速度,斜率的正负表示速度方向,所以A物体运动方向不变,故A错误;x-t图像的斜率表示速度,由题图可知,0~6 s内B物体的速度逐渐增大,故B错误;由题图可知,0~5 s内A物体的位移大于B物体的位移,由公式eq \(v,\s\up6(-))=eq \f(x,t)可知,A物体的平均速度大于B物体的平均速度,故C错误;0~6 s内存在某时刻两图像斜率的绝对值相等,即存在某时刻两物体的速度大小相等,故D正确。
2.ETC自动道路缴费系统推行后,有效地缓解了高速公路收费站的拥堵现象。若某汽车在高速上正常行驶速度为30 m/s,沿该平直公路通过收费站ETC通道时,其速度随时间变化的关系如图2所示,则ETC通道对该车行驶产生的时间延误为( )
图2
A.8 s B.20 s C.26 s D.40 s
答案 B
解析 根据v-t图像与横轴所围面积表示位移知,汽车通过ETC通道的位移为x=eq \f(30+5,2)×(6-1) m+5×(14-6) m+eq \f(5+30,2)×(41-14) m=600 m;没有收费站时,汽车所用时间为t=eq \f(x,v)=eq \f(600,30) s=20 s,所以ETC通道对该车行驶产生的时间延误为Δt=(41-1-20)s=20 s,B正确,A、C、D错误。
3.如图3所示,直线a1和曲线b1分别是在平直公路上行驶的汽车a和b的速度—时间(v-t)图线,t1时刻两车经过同一位置,由图可知( )
图3
A.在t2时刻,a车追上b车
B.在t1到t2这段时间内,b车的平均速度比a车的大
C.在t1到t2这段时间内,b车的平均速度为eq \f(v1+v2,2)
D.在t1到t2这段时间内,b车的加速度一直比a车的大
答案 B
解析 t1时刻两车经过同一位置,t1到t2这段时间内b车位移大,所以b车在前,故选项A错误;t1到t2这段时间内b车位移大,时间相同,所以b车平均速度大,故选项B正确;t1~t2时间,曲线b1与t轴所围的面积表示位移,可知,这段时间内b车平均速度大于eq \f(v1+v2,2),故选项C错误;图像斜率表示加速度,可以看出b车的加速度先减小,然后反向增大,并非一直比a车的大,故选项D错误。
4.一质点的位移—时间图像如图4所示,能正确表示该质点的速度v与时间t关系的图像是下列图中的( )
图4
答案 A
解析 质点在开始一段时间内的x-t图像是一条直线,其斜率不变且为负值,表示质点做匀速直线运动,速度方向与规定的正方向相反;在第二段时间内,质点处于静止状态,速度为零;在第三段时间内,图线的斜率不变且为正值,即速度不变且为正值;在第四段时间内,质点静止在出发点。综上可知,质点的v-t图像是图A,故选项A正确。
对点练2 “数学思维”分析非常规图像问题
5.如图5为物体做直线运动的图像,下列说法正确的是( )
图5
A.甲图中,物体在0~t0这段时间内的位移小于eq \f(1,2)v0t0
B.乙图中,物体的加速度为2 m/s2
C.丙图中,阴影面积表示t1~t2时间内物体的加速度变化量
D.丁图中,t=3 s时物体的速度为25 m/s
答案 D
解析 由v-t图线与坐标轴围成的面积表示位移,可知题图甲中,物体在0~t0这段时间内的位移大于eq \f(1,2)v0t0eq \b\lc\(\rc\)(\a\vs4\al\c1(平均速度大于\f(1,2)v0)),A错误;根据v2=2ax可知,2a=1 m/s2,则物体的加速度为0.5 m/s2,B错误;根据Δv=at可知,题图丙中阴影部分的面积表示t1~t2时间内物体的速度变化量,C错误;由x=v0t+eq \f(1,2)at2可得eq \f(x,t)=v0+eq \f(1,2)at,结合题图丁可知eq \f(1,2)a=eq \f(10,2) m/s2=5 m/s2,即a=10 m/s2,则v0=
-5 m/s,故t=3 s时物体的速度为v3=(-5+10×3)m/s=25 m/s,D正确。
6.汽车中的ABS系统在汽车制动时,能防止车轮抱死,可以减小刹车距离,增强刹车效果。实验小组通过实验,研究有ABS系统和无ABS系统两种情况下的匀减速制动距离,测试的初速度均为60 km/h。根据图6的图线及数据,可以推断出两种情况下汽车刹车的加速度大小之比a有∶a无等于( )
图6
A.4∶3 B.3∶4 C.3∶2 D.2∶3
答案 A
解析 根据v2=2ax得a=eq \f(v2,2x),因为初速度相等时,刹车的距离之比为3∶4,则平均加速度之比a有∶a无=4∶3,故A正确。
对点练3 追及相遇问题
7.自动驾驶汽车又称无人驾驶汽车,是一种通过电脑系统实现无人驾驶的智能汽车。某次自动驾驶汽车以恒定的加速度启动,同时一辆货车以恒定速度从其旁边驶过,自动驾驶汽车再次与货车相遇之前已达到最大速度,则下列图像正确的是( )
答案 D
解析 v-t图像的斜率代表加速度,由于自动驾驶汽车以恒定加速度启动,则自动驾驶汽车加速时的v-t图线为直线,A错误;v-t图线与t轴围成的面积表示位移,由题可知自动驾驶汽车再次与货车相遇之前已达到最大速度,B项中t0时刻自动驾驶汽车刚好达到最大速度,且由图像中几何关系可知此时两车位移相等,则此时相遇,B错误;x-t图像的斜率表示速度大小,图线交点表示两车位移相同,C项中自动驾驶汽车与货车相遇时其速度还未达到最大,C错误;D项中两车x-t图线交点表示两车再次相遇,且自动驾驶汽车在再次相遇之前已经达到最大速度,D正确。
8.两辆完全相同的汽车,沿水平直路一前一后同向匀速行驶,速度均为v0,若前车突然以恒定的加速度刹车,在它刚停住时,后车以前车刹车时的加速度开始刹车。已知每辆车在刹车过程中所行驶的距离均为s,若要保证两车在上述情况中不相撞,则两车在匀速行驶时保持的距离至少为( )
A.s B.2s C.3s D.4s
答案 B
解析 两辆完全相同的汽车,刹车时加速度相同,刹车位移也相同,均为s,设加速度大小为a,前车刹车的时间为t=eq \f(v0,a),刹车位移为s=eq \f(veq \\al(2,0),2a),在此时间内,后车做匀速运动,位移为x=v0t=eq \f(veq \\al(2,0),a),所以x=2s,此后,后车刹车,刹车位移也为s,要保持两车在上述情况中不相撞,则两车在匀速行驶时保持的距离至少应为Δx=x+s-s=x=2s,故选项B正确,A、C、D错误。
B级 综合提升练
9.甲、乙两物体分别在水平面上做直线运动,取向右为正方向,它们运动的相关图像分别如图7甲、乙所示。已知乙的初速度为0,下列说法正确的是( )
图7
A.甲物体2 s时的运动方向发生变化
B.乙物体2 s时的运动方向发生变化
C.甲物体0~2 s内的平均速度与2~4 s内的平均速度相同
D.乙物体4 s时的位置与0时刻的位置相同
答案 A
解析 甲物体2 s时速度从负值变为正值,即运动方向发生变化,故A正确;已知乙的初速度为0,因a-t图像与时间轴围成的面积等于速度的变化量,可知乙物体在0~2 s时间内速度为负值,在2~4 s内速度变化量为正值,在t=4 s时速度减为零,但是在2~4 s内速度仍为负值,则2 s时的运动方向没有发生变化,故B错误;甲物体0~2 s内的平均速度与2~4 s内的平均速度大小相同,但是方向相反,故C错误;乙物体0~4 s内速度一直为负,则4 s时的位置与0时刻的位置不相同,故D错误。
10.(2023·辽宁大连一模)一辆汽车以20 m/s的速度在平直公路上行驶,某时刻司机发现前方施工需减速行驶,司机反应了0.2 s后才开始刹车,如图8所示为发现施工提示后的速度平方v2随位移x的变化关系。从司机发现前方施工提示至汽车速度减小到5 m/s的过程中,汽车的位移为( )
图8
A.37.5 m B.40 m C.41.5 m D.44 m
答案 C
解析 由运动学公式v2-veq \\al(2,0)=2ax,结合图像可知2a=k=-10 m/s2,汽车从开始减速到速度减至v=5 m/s过程中,汽车的位移为x1=eq \f(veq \\al(2,5)-veq \\al(2,0),2a)=37.5 m,司机反应了0.2 s,汽车运动的位移x2=4 m,所以从司机发现前方施工提示至汽车速度减小到5 m/s的过程中,汽车的位移为x=x1+x2=41.5 m,C正确。
11.(2023·安徽合肥模拟)强行超车是道路交通安全的极大隐患之一。如图9是汽车超车过程的示意图,汽车甲和货车均以36 km/h的速度在路面上匀速行驶,其中甲车车身长L1=5 m、货车车身长L2=8 m,货车在甲车前s=3 m处。若甲车司机开始加速从货车左侧超车,加速度大小为2 m/s2。假定货车速度保持不变,不计车辆变道的时间及车辆的宽度。求:
图9
(1)甲车完成超车至少需要多长时间;
(2)若甲车开始超车时,看到道路正前方的乙车迎面驶来,此时二者相距110 m,乙车速度为54 km/h。甲车超车的整个过程中,乙车速度始终保持不变,请通过计算分析,甲车能否安全超车。
答案 (1)4 s (2)不能安全超车
解析 (1)设甲车经过时间t刚好完成超车,
在时间t内
甲车位移x1=v1t+eq \f(1,2)at2
货车位移x2=v2t
根据几何关系有x1=x2+L1+L2+s
代入数据解得t=4 s
则甲车完成超车至少需要的时间为4 s。
(2)假设甲车能安全超车,在4 s内,
甲车位移x1=v1t+eq \f(1,2)at2=56 m
乙车位移x3=v3t=60 m
由于x1+x3=116 m>110 m,故甲车不能安全超车。
12.在足球比赛中,经常使用“边路突破,下底传中”的战术,即攻方队员带球沿边线前进,到底线附近进行传中。某足球场长90 m、宽60 m,如图10所示。攻方前锋在中线处将足球沿边线向前踢出,足球的运动可视为在地面上做初速度为12 m/s的匀减速直线运动,加速度大小为2 m/s2,试求:
图10
(1)足球从开始做匀减速运动到停下来的位移;
(2)足球开始做匀减速直线运动的同时,该前锋队员沿边线向前追赶足球,他的启动过程可以视为初速度为0,加速度为2 m/s2的匀加速直线运动,他能达到的最大速度为8 m/s。该前锋队员距离足球的最远距离是多少?并求出至少经过多长时间他能追上足球?
答案 (1)36 m (2)18 m 6.5 s
解析 (1)设足球做匀减速运动的时间为t0,逆向思维,则t0=eq \f(v0,a1)=6 s
位移为x=eq \f(1,2)a1teq \\al(2,0)=36 m。
(2)前锋队员先加速后匀速,足球匀减速,当二者速度相等时,距离最远,设经过t秒速度相等,则
v0-a1t=a2t
解得t=3 s
此时二者速度均为v=a2t=6 m/s
足球向前的位移x1=v0t-eq \f(1,2)a1t2=27 m
前锋队员的位移x2=eq \f(v2,2a2)=9 m
最远距离Δx=x1-x2=18 m
前锋队员从起跑到达到最大速度的时间和位移分别为
t1=eq \f(v2,a2)=4 s
x3=eq \f(v2,2)t1=16 m
之后前锋队员做匀速运动,假设追上足球时,足球已停止,其匀速运动位移x4=x-x3=20 m
则做匀速运动的时间
t2=eq \f(x4,v2)=2.5 s
前锋队员追上足球的时间
t3=t2+t1=6.5 s>6 s
假设合理。x-t图像
v-t图像
图像
举例
意义
倾斜直线表示匀速直线运动;曲线表示变速直线运动
倾斜直线表示匀变速直线运动;曲线表示变加速直线运动
运动
情况
甲做匀速直线运动,乙做速度逐渐减小的直线运动
丙做匀加速直线运动,丁做加速度逐渐减小的变加速直线运动
交点和
“面积”
两条图线的交点表示相遇;图线与横轴所围面积无意义
两条图线的交点表示t2时刻速度相等,图线与横轴所围面积表示位移
位移
0~t1时间内甲、乙位移相等
0~t2时间内丁的位移大于丙的位移
平均
速度
0~t1时间内甲、乙平均速度相等
0~t2时间内丁的平均速度大于丙的平均速度
情境
分析法
抓住“两物体能否同时到达空间某位置”这一关键,认真审题,挖掘题目中的隐含条件,建立一幅物体运动关系的情境图
函数
判断法
设相遇时间为t,根据条件列方程,得到关于位移x与时间t的函数关系,由此判断两物体追及或相遇情况
图像
分析法
将两个物体运动的速度—时间关系或位移—时间关系画在同一图像中,然后利用图像分析求解相关问题
新高考物理一轮复习专题1.2 运动图像问题 追及相遇问题 精品练习(含解析): 这是一份新高考物理一轮复习专题1.2 运动图像问题 追及相遇问题 精品练习(含解析),共23页。
高考物理一轮复习第一章第3节运动图像追及和相遇问题讲义 含解析: 这是一份高考物理一轮复习第一章第3节运动图像追及和相遇问题讲义 含解析,共14页。试卷主要包含了运动图像[注1],追及和相遇问题等内容,欢迎下载使用。
高考物理一轮复习课时训练专题02运动图像追及和相遇问题(含解析): 这是一份高考物理一轮复习课时训练专题02运动图像追及和相遇问题(含解析),共6页。试卷主要包含了 选择题,计算题等内容,欢迎下载使用。












