

2023-2024学年高二数学上学期期中模拟试题02(新高考地区专用,测试范围:第1-2章)(Word版附解析)
展开(考试时间:150分钟 试卷满分:150分)
注意事项:
1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答第Ⅰ卷时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。写在本试卷上无效。
3.回答第Ⅱ卷时,将答案写在答题卡上。写在本试卷上无效。
4.测试范围:第1-2章(人教版选择性必修一)。
5.考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷
一、单项选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.(2023·湖北武汉第十七中学高二期中)直线在x轴上的截距是( )
A.1B.C.D.2
【答案】C
【解析】将代入直线方程,可得,解得,故选C.
2.已知直线,若直线与垂直,则的倾斜角为( )
A.B.C.D.
【答案】A
【解析】因为直线与垂直,且,所以,解得,
设的倾斜角为,,所以,故选A.
3.直线的一个方向向量为,平面的一个法向量为,则( )
A.B.
C.或D.与的位置关系不能判断
【答案】B
【解析】直线的一个方向向量为,平面的一个法向量为,
显然它们共线,所以.故选B.
4.(2023·福建厦门高二期中)若点在圆的外部,则实数的取值范围是( )
A.B.
C.D.
【答案】C
【解析】因为点在圆的外部,
所以,解得,故选C.
5.如图所示,在平行六面体中,为与的交点,若,,,则( )
A.B.C.D.
【答案】D
【解析】由题意,因为为与的交点,所以也为与的中点,
因此,故选D.
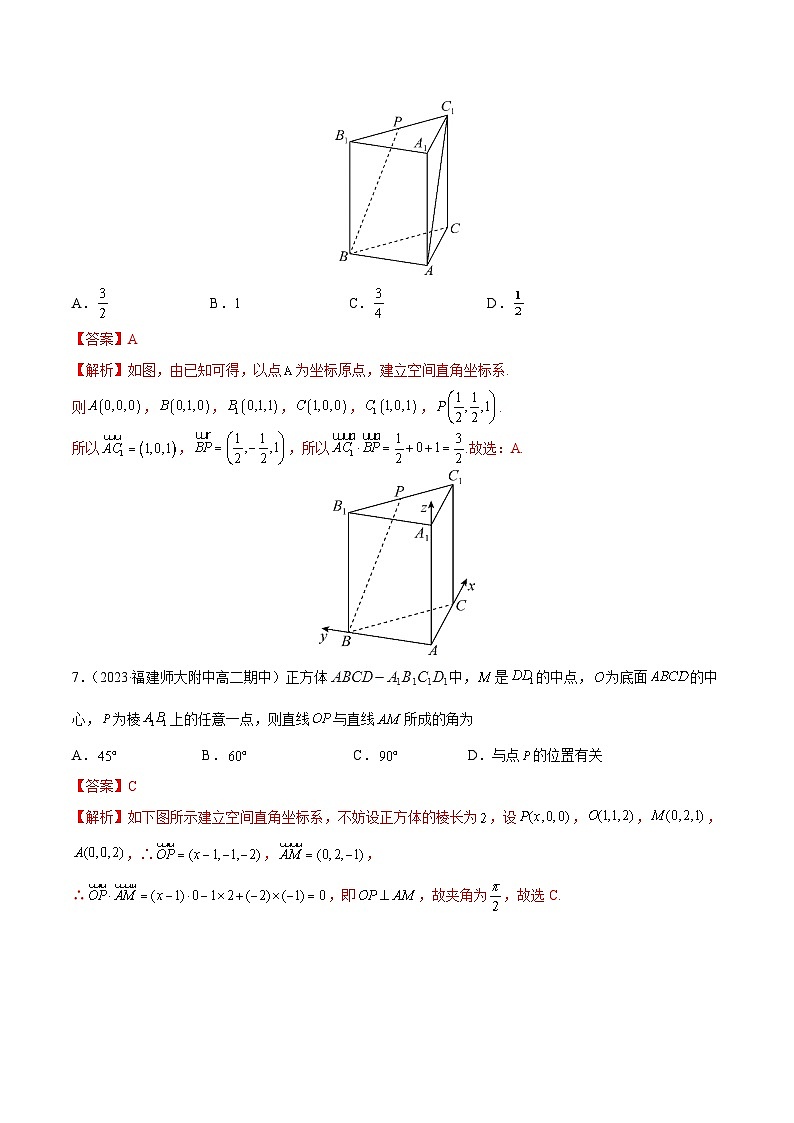
6.《九章算术》是我国东汉初年编订的一部数学经典著作,其在卷第五《商功》中记载“斜解立方,得两堑堵”,堑堵是底面为直角三角形的直三棱柱.如图,在堑堵中,,P为的中点,则( )
A.B.1C.D.
【答案】A
【解析】如图,由已知可得,以点为坐标原点,建立空间直角坐标系.
则,,,,,.
所以,,所以.故选:A.
7.(2023·福建师大附中高二期中)正方体中,是的中点,为底面的中心,为棱上的任意一点,则直线与直线所成的角为
A. B. C. D.与点的位置有关
【答案】C
【解析】如下图所示建立空间直角坐标系,不妨设正方体的棱长为,设,,,,∴,,
∴,即,故夹角为,故选C.
8.阿波罗尼斯是古希腊著名数学家,与阿基米德、欧几里得并称为亚历山大时期数学三巨匠,他研究发现:如果一个动点到两个定点的距离之比为常数(,且),那么点的轨迹为圆,这就是著名的阿波罗尼斯圆.若点到,的距离之比为,则点到直线的距离的最小值为( )
A.B.
C.D.
【答案】A
【解析】设,则,化简得,
即点的轨迹方程为以为圆心,为半径的圆,
则点到直线的距离的最小值为圆心到直线的距离减去半径,
即,点到直线的距离最小值为.
故选:A
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,部分选对的得2分,有选错的得0分.
9.(2023·四川省武胜烈面中学校高二期中)对于直线,下列说法正确的有( )
A.直线l过点B.直线l与直线垂直
C.直线l的一个方向向量为D.直线l的倾斜角为45°
【答案】AB
【解析】直线化成斜截式为,所以当时,,A对;直线l的斜率为﹣1,倾斜角为135°,D错;直线的斜率为1,,所以两直线垂直,B对;直线l的一个方向向量为,C错.故选AB.
10.已知空间三点,,,则下列说法正确的是( )
A.B.C. D.
【答案】AC
【解析】因为,,,
所以
所以,,,所以不共线,故选AC
11.(2023·江苏盐城高二期中)圆和圆的交点为,,则( )
A.公共弦所在直线的方程为
B.线段中垂线的方程为
C.公共弦的长为
D.两圆圆心距
【答案】ABD
【解析】①,②,用①减去②即得到公共弦所在直线的方程为,故A正确;
把圆化为标准方程得,圆心为,半径为 ,把圆化为标准方程为,圆心为,,线段中垂线即为圆心与圆心两点构成的直线为,故B正确;
圆心到公共弦所在直线的距离为,故公共弦的长为,故C错误;
圆心到圆心的距离,故D正确. 故选ABD.
12.已知正方体的棱长为1,下列四个结论中正确的是( )
A.直线与直线所成的角为
B.直线与平面所成角的余弦值为
C.平面
D.点到平面的距离为
【答案】ABC
【解析】如图以为原点,分别以所在的直线为轴建立空间直角坐标系,则, ,,,
对于A:,,
因为,所以,即,直线与直线所成的角为,故选项A正确;
对于C:因为 ,,,
所以,,所以,,
因为,所以平面,故选项C正确;
对于B:由选项C知:平面,所以平面的一个法向量,因为,所以,即直线与平面所成角的正弦值为,所以直线与平面所成角的余弦值为,故选项B正确;
对于D:因为,平面的一个法向量,
,,
故,令,则,故,
所以点到平面的距离,故D不正确,故选ABC.
第Ⅱ卷
三、填空题:本题共4小题,每小题5分,共20分.
13.直线与平行,则它们的距离是
【答案】
【解析】直线可化为直线,
又,且,
所以它们的距离.
14.求过点且与圆相切的直线方程为 .
【答案】x=4或3x+4y=0
【解析】当直线的斜率存在时,可设直线方程为y+3=k(x-4),即kx-y-4k-3=0,
由题意得,
解得k=,此时直线方程为3x+4y=0,
当直线的斜率不存在时,直线方程为x=4
此时圆心 到直线x=4的距离为3,所以直线与圆相切,符合题意.
15.(2023·黑龙江实验中学高二月考)已知点在直线上,则的最小值为 .
【答案】2
【解析】可以理解为点到点的距离,
又∵点在直线上,
∴的最小值等于点到直线的距离,
且.
16.如图,在三棱柱ABC-A1B1C1中,所有棱长均为1,且AA1⊥底面ABC,则点B1到平面ABC1的距离为 .
【答案】
【解析】以点C为坐标原点,建立空间直角坐标系如图所示,
则,
所以,, ,
设平面ABC1的法向量为,则,即,
令,则,故,
所以点B1到平面ABC1的距离为.
.
四、解答题:本题共6小题,共70分.第17题10分,其他每题12分,解答应写出文字说明、证明过程或演算步骤.
17.(2023·浙江省镇海高中高二期中)已知的顶点,重心.
(1)求线段BC的中点坐标;
(2)记的垂心为H,若B、H都在直线上,求H的坐标.
【解析】(1)设中点,
因为为的重心,且,
所以,即
所以,所以中点
(2)因为的方程为,且为的垂心
所以即,所以
所以直线的方程为:,即
所以设点,又因为的中点,设则
即
又因为点在直线上,即,所以
所以,所以,则边上的高线为
而点也在直线:上,所以点的坐标即为与的交点
即.
18.(2023·江苏扬州高二期中)已知一条动直线,
(1)求证:直线恒过定点,并求出定点P的坐标,并求出点到动直线的最大距离.
(2)若直线与x.y轴的正半轴分别交于A,B两点,O为坐标原点,是否存在直线满足下列条件:①的周长为12;②的面积为6,若存在,求出方程;若不存在,请说明理由.
【解析】(1)将直线方程变形为,
由,可得,
因此,直线恒过定点.
当垂直与直线时,点到直线的距离最大,
因为,所以直线的斜率为,
所以,故,
所以直线的方程为,
点到直线的距离为,
所以点到动直线的最大距离为;
(2)假设存在点和点满足要求,则
,解方程可得或,
所以直线的方程为或,
故存在直线或.
19.(2023·河南省开封高中高二期中)在下列所给的三个条件中任选一个,补充在下面的问题中,并加以解答.
①与直线垂直;②过点;③与直线平行.
问题:已知直线过点,且___________.
(1)求直线的一般式方程;
(2)若直线与圆相交于点,,求弦的长.
【解析】方案一选条件①.
(1)因为直线的斜率为,又直线与直线垂直,
所以直线的斜率为,
依题意,直线的方程为,即.
(2)圆的圆心到直线的距离为.
又圆的半径为,所以.
方案二选条件②.
(1)因为直线过点及,
所以直线的方程为,即.
(2)圆的圆心到直线的距离为.
又圆的半径为,所以.
方案三选条件③.
(1)因为直线的斜率为,直线与直线平行,
所以直线的斜率为
依题意,直线的方程为,即.
(2)圆的圆心到直线的距离为.
又圆的半径为,所以.
20.如图,四棱锥中,底面是直角梯形,,,,.
(1)求证:平面;
(2)求直线与平面所成角的正弦值.
【解析】(1)证明:由于,,所以,
由于,,、平面,所以平面,
平面,由平面,得.
取的中点,连接,
因为底面是直角梯形,且,,
故四边形为矩形,且且,,
所以在中,,,,即,
由于,、平面,所以平面.
(2)解:平面,,以点为坐标原点,、、所在直线分别为、、轴建立如下图所示的空间直角坐标系,
则、、、、,
,,,
设平面的法向量为,则,取,可得,
所以,.
所以,直线与平面所成角的正弦值为.
21.如图,四棱锥中,四边形是矩形,平面,,是的中点,是的中点.
(1)证明:平面;
(2)若,,求平面与平面夹角的余弦值.
【解析】(1)取中点,连接,
分别为的中点,,,
因为四边形是矩形,是的中点,所以且,
故且,则四边形为平行四边形,
,又面,平面,
所以平面.
(2)设,则,
因为,所以由勾股定理得,则是等腰直角三角形,
又平面,
故以中点为原点,过点和平行的直线为轴,如图建立空间直角坐标系,
则,,,,
则,,,
设是面的一个法向量,则有,
取,则,故,
设是面的一个法向量,则有,
取,则,故,
记平面与平面夹角为,
则,
所以平面与平面夹角的余弦值.
22.已知正四棱柱中,,,点为棱的中点.
(1)求二面角的余弦值;
(2)连接,若点为直线上一动点,求当点到直线距离最短时,线段的长度.
【解析】(1)解:以为原点,、、所在直线分别为、、轴建立如图所示的空间直角坐标系,
则、、、、、,
则,,,
设平面的法向量为,则,
取,则,
设平面的法向量为,则,
取,可得,,
由图可知,二面角的平面角为锐角,
故二面角的余弦值为.
(2)解:设,其中,
则,
令,设点到直线的距离为,
则,
故当时,取最小值,此时.
2023-2024学年高二数学上学期期中期末挑战满分冲刺卷(人教A版2019选择性必修第二册,浙江专用)期末测试卷02(测试范围:第1-4章数列)(Word版附解析): 这是一份2023-2024学年高二数学上学期期中期末挑战满分冲刺卷(人教A版2019选择性必修第二册,浙江专用)期末测试卷02(测试范围:第1-4章数列)(Word版附解析),共20页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
2023-2024学年高二上学期期末数学模拟卷(新高考地区专用,测试范围:空间向量与立体几何、直线与圆、圆锥曲线、数列)02(Word版附解析): 这是一份2023-2024学年高二上学期期末数学模拟卷(新高考地区专用,测试范围:空间向量与立体几何、直线与圆、圆锥曲线、数列)02(Word版附解析),共20页。试卷主要包含了本试卷分第Ⅰ卷两部分,测试范围,定义“等方差数列”等内容,欢迎下载使用。
2023-2024学年高二上学期期末数学模拟卷(新高考地区专用,测试范围:空间向量与立体几何、直线与圆、圆锥曲线、数列)03(Word版附解析): 这是一份2023-2024学年高二上学期期末数学模拟卷(新高考地区专用,测试范围:空间向量与立体几何、直线与圆、圆锥曲线、数列)03(Word版附解析),共14页。试卷主要包含了本试卷分第Ⅰ卷两部分,测试范围,在平行六面体中,点E满足,则,已知直线,则,已知曲线,下列说法正确的有等内容,欢迎下载使用。












