山西省朔州市多校联考2023-2024学年九年级上学期期中数学试题

这是一份山西省朔州市多校联考2023-2024学年九年级上学期期中数学试题，共42页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

说明：共三大题，23 小题，满分 120 分，作答时间 120 分钟.
一、选择题（本大题共 10 个小题，每小题 3 分，共 30 分.在每个小题给出的四个选项中，只有一项符合题目要求，请把正确答案的代号填在下表中）
下列函数是二次函数的是（）
B. C.D.
刺绣，古代称之为针绣，是用绣针引彩线，将设计的花纹在纺织品上刺绣运针，以绣迹构成花纹图案的一 种工艺，是中国民间传统手工艺之一.下列四个刺绣花纹图案中，既是轴对称图形又是中心对称图形的是（）
A. B. C. D.
若二次函数的图象开口向下，则实数 a 的取值范围是（）
A. B. C. D.
若，是方程的两个根，则（）
A. B. C.D.
如图，AB 为的直径，半径 OA 的垂直平分线交于点 C，D，交 AB 于点 E，若，则 CD 的长为（）
A. B. 4C. D. 6
下表是几组二次函数的自变量 x 与函数值 y 的对应值
那么方程的一个解 x 的取值范围是（）
A. B. C. D.
山西醋甲天下，为开拓醋的养生功能，某醋厂开发出樱桃醋.为打开市场，该樱桃醋经过两次降价，售价由
x
1
1.1
1.2
1.3
1.4
y
－1
－0.49
0.04
0.59
1.16
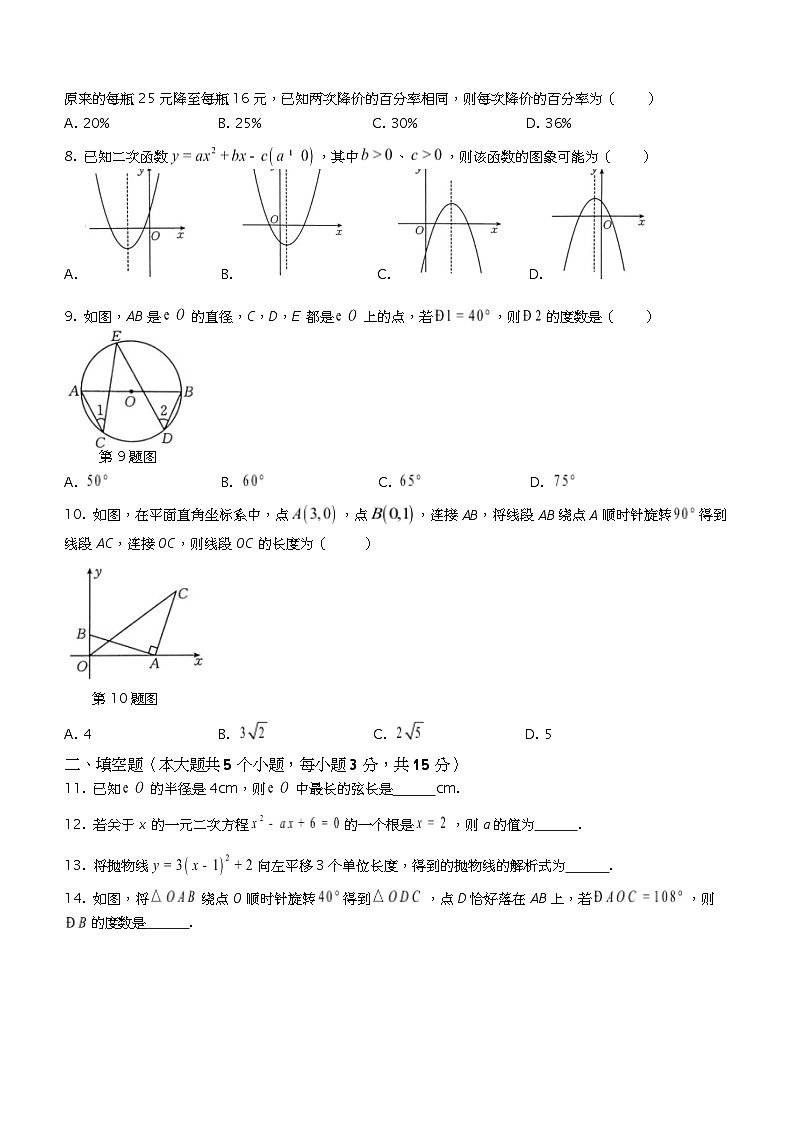
原来的每瓶 25 元降至每瓶 16 元，已知两次降价的百分率相同，则每次降价的百分率为（）
A. 20%B. 25%C. 30%D. 36%
已知二次函数，其中、，则该函数的图象可能为（）
A. B. C. D.
如图，AB 是的直径，C，D，E 都是上的点，若，则的度数是（）
第 9 题图
A. B. C. D.
如图，在平面直角坐标系中，点，点，连接 AB，将线段 AB 绕点 A 顺时针旋转得到线段 AC，连接 OC，则线段 OC 的长度为（）
第 10 题图
A. 4B. C. D. 5
二、填空题（本大题共 5 个小题，每小题 3 分，共 15 分）
已知的半径是 4cm，则中最长的弦长是cm.
若关于 x 的一元二次方程的一个根是，则 a 的值为.
将抛物线向左平移 3 个单位长度，得到的抛物线的解析式为.
如图，将绕点 O 顺时针旋转得到，点 D 恰好落在 AB 上，若，则 的度数是.
第 14 题图
如图，在中，D 是的中点，AC 与 BD 相交于点 E，若 E 是 BD 的中点，，则 AC 的长是.
第 15 题图
三、解答题（本大题共 8 个小题，共 75 分.解答应写出文字说明，证明过程或演算步骤）
16.（本题共 2 个小题，每小题 5 分，共 10 分）
应点 D 恰好落在边 BC 上，求 BD 的长.
18.（本题 9 分）
已知等腰腰和底边的长是关于 x 的一元二次方程的两个实数根.
当时，求的周长.
若为等边三角形，求 k 的值. 19.（本题 9 分）
如图，抛物线经过直线与坐标轴的两个交点 A，B，此抛物线与 x 轴的另一个交点为
C.
解方程：
已知二次函数
.
的图象经过
，求此函数的解析式.
17.（本题 7 分）
如图，在中，
，
，将绕点 A 按逆时针方向旋转得到，若点 B 的对
求此抛物线的解析式.
求的面积. 20.（本题 8 分）
如图 1，太原地铁 2 号线工程建设者在施工时意外发现一座石拱桥.经考证，该石拱桥是明清时期太原府城大北门外的镇远桥，是当时城防交通体系的重要实物遗存.图 2 是根据某石拱桥的实物图画出的几何图形，桥的
主桥拱是圆弧形，设所在圆的圆心为 O，拱顶为点 C，交 AB 于点 D，连接 OB.当桥下水面宽 时，.
图 1图 2
求这座石拱桥主桥拱的半径.
有一条宽为 7m，高出水面 1m 的矩形渔船，请你判断一下，此渔船能否顺利通过这座拱桥？并说明理由.
21.（本题 7 分）阅读与思考
下面是一位同学的数学学习笔记，请仔细阅读并完成相应任务.
关于圆的引理
古希腊数学家、物理学家阿基米德流传于世的数学著作有 10 余种，下面是《阿基米德全集》的《引理集》中记载的一个命题：
如图 1，AB 是
的弦，点 C 在
上，
于点 D，在弦 AB 上取点 E，使
，F 是
上的一点，且
，连接 BF，则
.
小颖对这个问题很感兴趣，经过思考，写出了下面的证明过程：
证明：如图 2，连接 CA，CE，CF，BC.
∵
∴
于点 D，
，
，
∴
.
∵
∴
，
（依据 1），
.
∵四边形 ABFC 内接于，
∴.（依据 2）
……
图 1
图 2
上述证明过程中的依据 1 为，依据 2 为.
将上述证明过程补充完整. 22.（本题 12 分）综合与实践
2023 年世界女排联赛总决赛于北京时间 7 月 13 日至 7 月 17 日在美国阿灵顿展开了最终对决.某排球场的长度为 18m，球网在场地中央且高度为 2.24m，排球出手后的运动路线可以看作是抛物线的一部分，建立如图所示的平面直角坐标系，排球运动过程中的竖直高度 y（单位：m）与水平距离 x（单位：m）近似满足函数
关系.
主攻手第一次发球时，测得水平距离 x 与竖直高度 y 的几组数据如下.
根据上述数据，求抛物线解析式.
在（1）的条件下，判断主攻手第一次发球能否过网，并说明理由.
主攻手第二次发球时，排球运动过程中的竖直高度 y（单位：m）与水平距离 x（单位：m）近似满足函数关系，判断主攻手此次发球是否出界，并说明理由.
23.（本题 13 分）综合与探究
水平距离
x/m
0
2
4
6
11
12
竖直高度
y/m
2.38
2.62
2.7
2.62
1.72
1.42
已知四边形 ABCD 是菱形，，，的两边分别与射线 CB，DC 相交于点 E，F，且.
【初步感知】
当 E 是线段 CB 的中点时（如图 1），AE 与 EF 的数量关系为.
【深入探究】
图 1图 2图 3
2024 届九年级期中综合评估数学参考答案
1. C2. D3. A4. B5. C6. B7. A8. C9. A10. D
11. 812. 513.14.
15. 提示：如图，连接 DO，交 AC 于点 F.
∵D 是的中点，
∴，，.
（2）如图 2，将图 1 中的
绕点 A 顺时针旋转
，（1）中的结论还成立吗？说明理由.
【拓展应用】
（3）如图 3，将图 2 中的
绕点 A 继续顺时针旋转，当
时，求点 F 到 BC 的距离.
∵AB 是直径，∴
，∴
.
∵E 是 BD 的中点，∴
.
∵，
∴
，∴
.
∵，∴
，
∴，∴
，
∴
.
解：（1）∵，
∴，……3 分
解得，.……5 分
把代入得，……8 分
∴函数解析式为.……10 分
解：由旋转得.……2 分
∵，
∴是等边三角形，……4 分
∴，
∴BD 的长为 3.……7 分
解：（1）当时，一元二次方程为，解得或.……2 分
∵是等腰三角形，
∴三边长为 4，4，2 或 2，2，4（舍去），……4 分
∴的周长.……5 分
（2）∵为等边三角形，
∴方程有两个相等的实数根.……6 分
，解得，
∴抛物线的解析式为.……5 分
∴
，……8 分
解得
19.
.……9 分
解：（1）当
时，
，则.
当
时，
，解得
，则
.
把
，
代入
得
（2）当时，，解得，，则，
∴.……9 分
20. 解：（1）∵，∴，
，
设主桥拱半径为 R，由题意可知，，
∴，.……1 分
∵
∴，
∴，……2 分
解得，
∴这座石拱桥主桥拱的半径为 5m.……4 分
（2）此渔船不能顺利通过这座拱桥.……5 分
理由：如图，设 MN 为该渔船的上端，连接 ON.
∵，船舱顶部为长方形并高出水面 1m，
∴，
∴.……6 分
在中，由勾股定理得，……7 分
∴，
∴此渔船不能顺利通过这座桥.……8 分
解：（1）在同圆中相等的弧所对的弦相等；圆内接四边形的对角互补.……4 分
，
∴，……6 分
（2）证明：∵
，
∴
.……5 分
在和
中，
∴.……7 分
解：（1）由表中数据可得顶点坐标为，
∴.
把代入得，解得，
∴抛物线解析式为.……4 分
不能.……5 分
理由：当时，，
∴主攻手第一次发球不能过网.……8 分
没有出界.……9 分
理由：第二次发球，
令，则，
解得（舍），.……10 分
∵，
∴主攻手此次发球没有出界.……12 分
解：（1）.……3 分
成立.……4 分
理由：如图 1，连接 AC.
∵四边形 ABCD 是菱形，
，
∴，……7 分
∴.
∴
∵
∴
，
，
.
是等边三角形，
∴
，.……5 分
∵
，
∴
.……6 分
在
和
中，
∵，∴是等边三角形，
∴.……8 分
图 1
如图 2，过点 A 作于点 G，过点 F 作于点 H，连接 AC.
当时，，∴.
在中，∵，，
∴，.……9 分
在中，∵，
∴，
∴.……10 分
由（2）可得，，
，
∴，……11 分
∴.
∵
，∴
∴
，
，……12 分
∴，即点 F 到 BC 的距离为.……13 分
图 2