数学华师大版第23章 图形的相似23.2 相似图形精品当堂达标检测题

这是一份数学华师大版第23章 图形的相似23.2 相似图形精品当堂达标检测题，共8页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（本大题共10小题，共30.0分。在每小题列出的选项中，选出符合题目的一项）
1.下列叙述正确的是( )
A. 任意两个等腰三角形相似B. 任意两个平行四边形相似
C. 任意两个矩形相似D. 任意两个正方形相似
2.下列两个图形一定相似的是( )
A. 两个菱形B. 两个矩形C. 两个正方形D. 两个等腰梯形
3.已知五边形ABCDE∽五边形A1B1C1D1E1，五边形ABCDE的最短边为2，最长边为6，五边形A1B1C1D1E1的最长边是12，则五边形A1B1C1D1E1的最短边是( )
A. 4B. 5C. 6D. 8
4.在如图所示的三个矩形中，相似的是( )
A. 甲和乙B. 甲和丙C. 乙和丙D. 甲、乙和丙
5.如图，三个矩形中相似的是
( )
A. 甲和乙B. 乙和丙C. 甲和丙D. 没有相似矩形
6.下列四个命题：①所有的正方形都相似；②所有的菱形都相似；③所有的矩形都相似；④边长相等的两个菱形相似，其中真命题的个数有( )
A. 1个B. 2个C. 3个D. 4个
7.如图，在长为8cm、宽为4cm的矩形中，截去一个矩形，使得留下的矩形(阴影部分)与原矩形相似，则留下矩形的面积是( )
A. 2cm2B. 4cm2C. 8cm2D. 16cm2
8.如图，把一张矩形纸片对折两次得到四个小矩形，如果每个小矩形都与原矩形相似，则原矩形纸片的长与宽之比为( )
A. 2:1B. 2:1C. 3:1D. 4:1
9.如图，矩形ABCD被分成5个正方形和2个小矩形后形成一个中心对称图形，如果矩形BEFG∽矩形ABCD，那么S矩形BEFGS矩形ABCD的值为( )
A. 12
B. 13
C. 14
D. 15
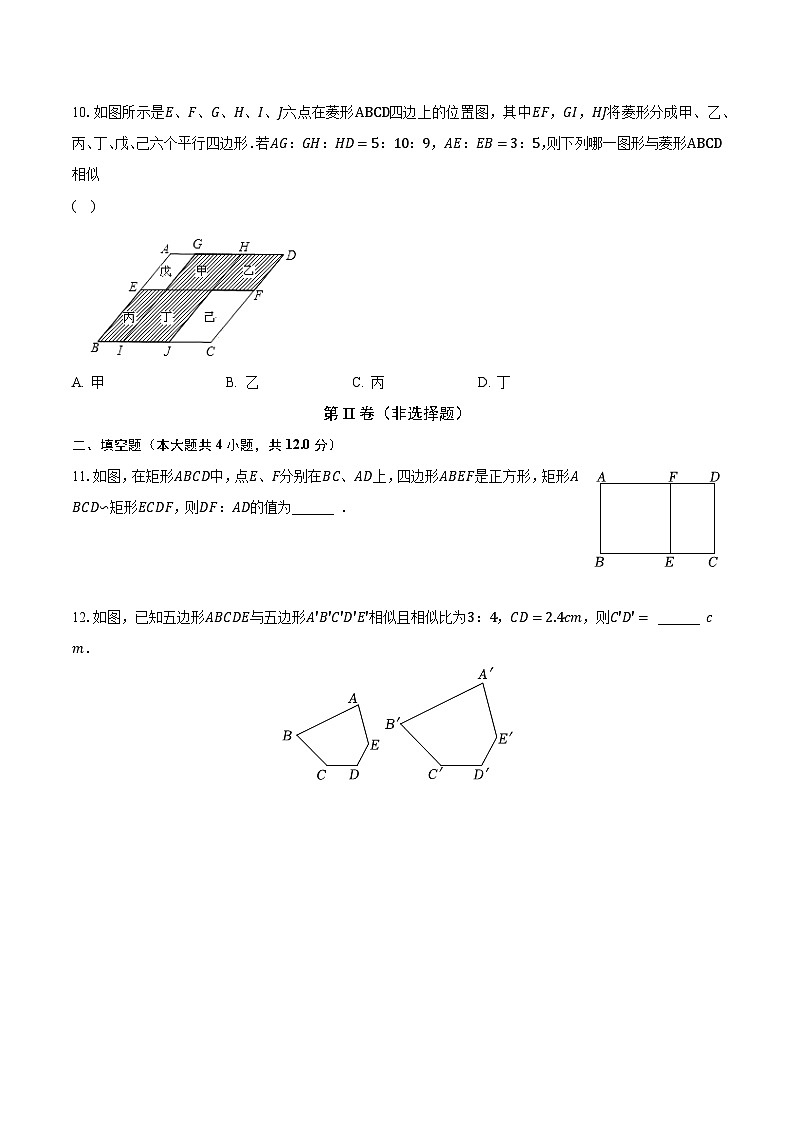
10.如图所示是E、F、G、H、I、J六点在菱形ABCD四边上的位置图，其中EF，GI，HJ将菱形分成甲、乙、丙、丁、戊、己六个平行四边形．若AG：GH：HD=5：10：9，AE：EB=3：5，则下列哪一图形与菱形ABCD相似
( )
A. 甲B. 乙C. 丙D. 丁
第II卷（非选择题）
二、填空题（本大题共4小题，共12.0分）
11.如图，在矩形ABCD中，点E、F分别在BC、AD上，四边形ABEF是正方形，矩形ABCD∽矩形ECDF，则DF：AD的值为______ ．
12.如图，已知五边形ABCDE与五边形A′B′C′D′E′相似且相似比为3：4，CD=2.4cm，则C′D′= ______ cm．
13.秋天红透的枫叶，总能牵动人们无尽的思绪，所以诗人杜牧说：“停车坐爱枫林晚，霜叶红于二月花”如图是两片形状相同的枫叶图案，则x的值为____．
14.如图所示的正方形网格中，每个小正方形的边长均为1，四边形ABCD的面积是 .若四边形EFGH与四边形ABCD相似，则四边形EFGH的面积是 ．
三、解答题（本大题共6小题，共48.0分。解答应写出文字说明，证明过程或演算步骤）
15.(本小题8.0分)
下面各点的位置在方格图上描出各点，再按A→B→C→D→A的顺序连起来，四边形ABCD是______ 形，图中每个小格的面积是1平方厘米，四边形ABCD的面积是______ 平方厘米．
A(1,2)，B(4,2)，C(5,4)，D(2,4)．
(1)请画出图形ABCD关于l的对称图形．
(2)请将图形ABCD按2：1放大画在右边．
16.(本小题8.0分)
我们知道，如果两个四边形的对应角相等，对应边成比例，那么这两个四边形叫做相似四边形．仅有对应角相等的两个四边形不一定相似，如正方形与两邻边长为1和2的矩形就不是相似四边形．
(1)仅有对应边成比例的两个四边形______相似(填“一定”、“不一定”或“一定不”)；
(2)如图，在四边形ABCD和四边形A′B′C′D′中，∠A=∠A′，∠B=∠B′，∠C=∠C′，ABA′B′=BCB′C′，求证：四边形ABCD∽四边形A′B′C′D′．
17.(本小题8.0分)
如图，矩形ABCD剪去一个以宽为边长的正方形ABFE后，剩下的矩形EFCD的长与宽的比与原矩形长与宽的比相等，求原矩形的长与宽的比．
18.(本小题8.0分)
在AB=30 m，AD=20 m的矩形花坛四周修筑小路．
(1)如果四周的小路的宽均相等，都是x，如图，那么小路四周所围成的矩形AˈBˈCˈDˈ和矩形ABCD相似吗？请说明理由；
(2)如果相对着的两条小路的宽均相等，宽度分别为x，y，如图，试问小路的宽x与y的比值为多少时，能使得小路四周所围成的矩形AˈBˈCˈDˈ和矩形ABCD相似？请说明理由．
19.(本小题8.0分)
在AB=20m，AD=30m的矩形花坛四周修筑小路．
(1)如果四周的小路的宽均相等，都是x，如图1，那么小路四周所围成的矩形A′B′C′D′和矩形ABCD相似吗?请说明理由;
(2)如果相对着的两条小路的宽均相等，宽度分别为x，y，如图2，试问小路的宽x与y的比值为多少时，能使得小路四周所围成的矩形A′B′C′D′和矩形ABCD相似?请说明理由．
20.(本小题8.0分)
阅读理解：给定一个矩形，如果存在另一个矩形，它的周长和面积分别是已知矩形的周长和面积的一半，则这个矩形是给定矩形的“减半”矩形．如图，矩形A1B1C1D1是矩形ABCD的“减半”矩形．请你解决下列问题：
(1)当矩形的长和宽分别为9和1时，它是否存在“减半”矩形？请做出判断，如果不存在，请说明理由；如果存在，请求出“减半”矩形的长宽．
(2)边长为a的正方形存在“减半”正方形吗？如果存在，求出“减半”正方形的边长；如果不存在，请说明理由．
答案和解析
1.【答案】D
【解析】解：A、任意两个等腰三角形不一定满足三边对应成比例，三个角分别对应相等，不一定相似，故选项不符合题意；
B、任意两个平行四边形不一定满足边对应成比例，四个角对应相等，不一定相似，故选项不符合题意；
C、任意两个矩形不一定满足边对应成比例，不一定相似，故选项不符合题意；
D、任意两个两个正方形满足相似图形的定义，故选项符合题意．
故选：D．
利用相似图形的定义逐一判断后即可得到答案．
本题考查了相似图形的定义，掌握“对应角相等、对应边成比例的两个图形相似”是解本题的关键．
2.【答案】C
【解析】解：A、两个菱形，对应边成比例，对应角不一定相等，不符合相似的定义，故不符合题意；
B、两个矩形，对应角相等，对应边不一定成比例，不符合相似的定义，故不符合题意；
C、两个正方形，对应角相等，对应边一定成比例，一定相似，故符合题意；
D、两个等腰梯形同一底上的角不一定相等，对应边不一定成比例，不符合相似的定义，故不符合题意；
故选：C．
根据相似图形的定义：对应角相等，对应边成比例的两个图形一定相似，结合选项，用排除法求解．
本题考查相似形的定义，熟悉各种图形的性质是解题的关键．
3.【答案】A
【解析】【分析】
本题考查了相似多边形的性质，掌握相似多边形对应边的比相等是解题的关键．根据相似多边形对应边的比相等即可求解．
【解答】
解：∵五边形ABCDE∽五边形A1B1C1D1E1，
五边形ABCDE的最短边为2，最长边为6，五边形A1B1C1D1E1的最长边是12，
∴2五边形A1B1C1D1E1的最短边=612，
∴五边形A1B1C1D1E1的最短边是4．
故选A．
4.【答案】A
【解析】【分析】
此题考查了相似多边形的判定．注意对应角相等，对应边成比例，则可判定多边形相似．
由都是矩形，可得所有对应角相等；然后由对应边成比例，即可判定三个矩形中相似的是甲和乙．
【解答】
解：∵都是矩形，
∴所有对应角相等；
∵甲与乙：84=63，故相似；
甲与丙：48≠34，故不相似；
∴乙与丙也不相似．
故选：A．
5.【答案】C
【解析】【分析】
此题考查了相似多边形的判定．注意对应角相等，对应边成比例，则可判定多边形相似.由都是矩形，可得所有对应角相等；然后由对应边成比例，即可判定三个矩形中相似的是甲和丙．
【解答】
解：∵都是矩形，
∴所有对应角相等，
∵甲与乙：64≠86，故不相似，
甲与丙：64.5=86=43，故相似，
∴乙与丙也不相似．
故选C．
6.【答案】A
【解析】解：①所有的正方形都相似，正确，是真命题，符合题意；
②所有的菱形对应边的比相等，但对应角不一定相等，故不一定都相似，错误，是假命题，不符合题意；
③所有的矩形的对应角相等，但对应边的比不一定相等，不一定都相似，故错误，是假命题，不符合题意；
④边长相等的两个菱形的对应边的比相等，但对应角不一定相等，不一定相似，故错误，是假命题，不符合题意．
真命题有1个，
故选：A．
利用相似图形的定义分别判断后即可确定正确的选项．
考查了命题与定理的知识，解题的关键是了解相似图形的定义，难度不大．
7.【答案】C
【解析】略
8.【答案】B
【解析】略
9.【答案】C
【解析】【分析】
本题考查了相似图形：把形状相同的图形称为相似图形．相似图形面积的比等于相似比的平方．也考查了中心对称图形．
设小正方形的边长为a，大正方形的边长为b，则AG=b，BG=b+a，BE=2b−a，CE=2b，利用相似的性质得到BGAD=BEAB，即b+a4b−a=2b−a2b+a，则b=32a，所以BG=52a，AD=5a，然后根据相似的性质求S矩形BEFGS矩形ABCD的值．
【解答】
解：设小正方形的边长为a，大正方形的边长为b，
则AG=b，BG=b+a，BE=2b−a，CE=2b，
∴AB=2b+a，BC=2b+2b−a=4b−a，
∵矩形BEFG∽矩形ABCD，
∴BGAD=BEAB，即b+a4b−a=2b−a2b+a，
∴b=32a，
∴BG=b+a=52a，AD=4b−a=5a，
∵矩形BEFG∽矩形ABCD，
∴S矩形BEFGS矩形ABCD=(BGAD)2=(52a5a)2=14．
故选：C．
10.【答案】B
【解析】【分析】
此题考查了相似菱形的判定：所有对应角相等，所有对应边的比相等．
根据题意可设AG=5x，GH=10x，HD=9x，AE=3y，EB=5y，可得：AB=8y，AD=24x，所以y=3x.因为EF，GI，HJ将菱形分成甲、乙、丙、丁、戊、己六个平行四边形，所以各四边形的对应角相等；又因为甲邻边边长为：3y，10x，即9x，10x，与菱形ABCD不相似；乙邻边边长为：3y，9x，即9x，9x，与菱形ABCD相似；丙邻边边长为：5y，5x，即15x，5x，与菱形ABCD不相似；丁邻边边长为：5y，10x，即15x，10x，与菱形ABCD不相似．
【解答】
解：根据题意可设AG=5x，GH=10x，HD=9x，AE=3y，EB=5y，
∴AB=8y，AD=24x，
∴y=3x．
∵EF，GI，HJ将菱形分成甲、乙、丙、丁、戊、己六个平行四边形，
∴各四边形的对应角相等；
∴甲邻边边长为：3y，10x，即9x，10x，与菱形ABCD不相似；
乙邻边边长为：3y，9x，即9x，9x，与菱形ABCD相似；
丙邻边边长为：5y，5x，即15x，5x，与菱形ABCD不相似；
丁邻边边长为：5y，10x，即15x，10x，与菱形ABCD不相似．
故选B．
11.【答案】3− 52
【解析】解：∵矩形ABCD∽矩形ECDF，
∴ADEC=ADEF，
设正方形ABEF的边长为x，EC=y，
则xy=x+yx，
∴x2−yx−y2=0，
∴x=y± 5y2，
∵x>0，y>0，
∴x=1+ 52y，
∴DF：AD=yx+y=y1+ 52y+y=3− 52．
故答案为：3− 52．
根据相似多边形的性质可得ADEC=ADEF，设正方形ABEF的边长为x，EC=y，那么xy=x+yx，求出x=1+ 52y，代入DF：AD=yx+y计算即可．
此题主要考查了相似多边形的性质，关键是掌握相似多边形对应边的比相等．
12.【答案】3.2
【解析】解：∵五边形ABCDE与五边形A′B′C′D′E′相似且相似比为3：4，
∴CDC′D′=34，
∵CD=2.4cm，
∴2.4C′D′=34，
∴C′D′=3.2(cm)，经检验符合题意；
故答案为：3.2
利用相似五边形的对应边之比等于相似比建立方程求解即可．
本题考查的是相似多边形的性质，熟记相似多边形的对应边的比即为相似比是解本题的关键．
13.【答案】11
【解析】解：由两个枫叶图案的形状相同，可知两个枫叶图案相似，
可得x22=1020，
解得x=11，
即x的值为11．
故答案为：11．
根据两个枫叶图案的形状相同，可知两个图形相似，再根据相似多边形的对应边的比等于相似比可得结果．
此题考查的是相似多边形的性质，即两个多边形相似，其对应边、对角线的比等于相似比．
14.【答案】92
818

【解析】解：根据题意，得
S四边形ABCD=2×4−12×1×2−12×1×2−1×1−12×1×1=92．
又∵四边形EFGH与四边形ABCD相似，
∴S四边形EFGH：S四边形ABCD=(FGBC)2=(64)2=94，
∴S四边形EFGH=92×94=818．
故答案为：92；818．
根据题意求得四边形ABCD的面积，再利用相似多边形的性质求解即可．
本题考查相似多边形的性质，三角形的面积等知识点，解题的关键是理解题意，灵活运用所学知识解决问题，属于中考常考题型．
15.【答案】平行四边 6
【解析】解：(1)四边形ABCD是平行四边形，四边形ABCD的面积=2×3=6；
如图，四边形A′B′C′D′为所作；
故答案为：平行四边，6；
(2)如图，四边形EFGH为所作．
先描点得到四边形，再根据平行四边形的判定方法可得到四边形ABCD为平行四边形，然后根据平行四边形的面积公式计算它的面积；
(1)利用网格特点和轴对称的性质分别画出点A、B、C、D关于直线l的对称点即可；
(2)向右平移四边形ABCD，然后把各边扩大2倍即可．
本题考查了作图−轴对称变换：先确定图形的关键点；再利用轴对称性质作出关键点的对称点；然后按原图形中的方式顺次连接对称点．也考查了相似变换．
16.【答案】不一定
【解析】解：(1)仅有对应边成比例的两个四边形不一定相似；
故答案为：不一定；
(2)连接AC，A′C′，如图，
∵∠B=∠B′，
∴△ABC∽△A′B′C′，
∴∠BAC=∠B′A′C′，∠BCA=∠B′C′A′，ABA′B′=BCB′C′=ACA′C′，
∵∠BAD=∠B′A′D′，∠BCD=∠B′C′D′，
∴∠DAC=∠BAD−∠BAC，
∠D′A′C′=∠B′A′D′−∠B′A′C′，
∴∠DAC=∠D′A′C′，
同理∠DCA=∠D′C′A′，
∴△ADC∽△A′D′C′，
∴ADA′D′=CDC′D′=ACA′C′，
∴ABA′B′=BCB′C′=CDC′D′=ADA′D′，
∵∠A=∠A′，∠B=∠B′，∠BCD=∠B′C′D′，
∴∠D=∠D′
∴四边形ABCD∽四边形A′B′C′D′．
(1)直接判断即可；
(2)只要证明各角对应相等、各边对应成比例即可．
本题考查的多边形的相似，解题的关键是证明各边对应成比例，各角对应相等．
17.【答案】解：设矩形的长是a，宽是b，
则DE=CF=a−b，
∵矩形ABCD∽矩形CDEF，
∴BCAB=CDCF，
即ab=ba−b，
整理得：a2−ab−b2=0，
两边同除以b2，得(ab)2−ab−1=0，
解得ab= 5+12或1− 52(舍去)．
∴长与宽的比为： 5+12．
【解析】利用相似多边形的相似比相等列出方程求解．
本题考查了相似多边形的性质，根据相似得到方程，解方程是解决本题的关键．
18.【答案】解： (1)如果四周的小路的宽均相等，那么小路四周所围成的矩形A′B′C′D′和矩形ABCD不相似;
设四周的小路的宽为x，
∵30+2x30=15+x15，20+2x20=10+x10，
∴30+2x30≠20+2x20，
∴小路四周所围成的矩形A′B′C′D′和矩形ABCD不相似;
(2)∵当30+2y30=20+2x20时，小路四周所围成的矩形A′B′C′D′和矩形ABCD相似，
解得：xy=23，
∴路的宽x与y的比值为2:3时，能使小路四周所围成的矩形A′B′C′D′和矩形ABCD相似．
【解析】此题考查了相似多边形的判定.此题难度适中，注意掌握数形结合思想与方程思想的应用．
(1)首先设四周的小路的宽为x，易得30+2x30≠20+2x20，则可判定：小路四周所围成的矩形A′B′C′D′和矩形ABCD不相似;
(2)由相似多边形的性质可得：当30+2y30=20+2x20时，小路四周所围成的矩形A′B′C′D′和矩形ABCD相似，继而求得答案．
19.【答案】解：(1)如果四周的小路的宽均相等，那么小路四周所围成的矩形A′B′C′D′和矩形ABCD不相似.理由如下：
设四周的小路的宽为x；
∵30+2x30=15+x15，20+2x20=10+x10=30+3x30；
∴30+2x30≠20+2x20；
∴小路四周所围成的矩形A′B′C′D′和矩形ABCD不相似;
(2)∵当20+2y20=30+2x30时，小路四周所围成的矩形A′B′C′D′和矩形ABCD相似，
解得xy=32；
∴小路的宽x与y的比值为32时，能使小路四周所围成的矩形A′B′C′D′和矩形ABCD相似．

【解析】此题考查了相似多边形的判定.此题难度适中，注意掌握数形结合思想与方程思想的应用．
(1)首先设四周的小路的宽为x，易得30+2x30≠20+2x20，则可判定：小路四周所围成的矩形A′B′C′D′和矩形ABCD不相似;
(2)由相似多边形的性质可得：当30+2y30=20+2x20时，小路四周所围成的矩形A′B′C′D′和矩形ABCD相似，继而求得答案．
20.【答案】解：(1)存在，理由如下：
设减半矩形的长为x，因为周长为1+9=10，则宽为5−x
由题知x(5−x)=92
解得：x1=5+ 72，x2=5− 72(舍去)
所以存在减半矩形，且长宽分别为5+ 72，5− 72
(2)不存在．
因为两个正方形是相似图形，当它们的周长比为12时，面积比必定是14，
所以正方形不存在“减半”正方形．
【解析】本题考查矩形的性质和相似图形的性质，关键知道相似图形的面积比，周长比的关系．
(1)存在，设“减半”矩形的长和宽分别为x和(5−x)，根据存在另一个矩形，它的周长和面积分别是已知矩形的周长和面积的一半，可列出方程求解．
(2)两个正方形是相似图形，周长比是12，面积比就应该是14，所以不存在“减半”正方形．