初中数学华师大版九年级上册24.1 测量优秀复习练习题

这是一份初中数学华师大版九年级上册24.1 测量优秀复习练习题，共4页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（本大题共10小题，共30.0分。在每小题列出的选项中，选出符合题目的一项）
1.兴趣小组的同学要测量树的高度．在阳光下，一名同学测得一根长为1米的竹竿的影长为0.4米，同时另一名同学测量树的高度时，发现树的影子不全落在地面上，有一部分落在教学楼的第一级台阶上，测得该影子的长为0.2米，一级台阶高为0.3米，如图所示，若此时落在地面上的影长为4.4米，则树高为
( )
A. 11.5米B. 11.75米C. 11.8米D. 12.25米
2.如图，小明想用太阳光测量房子AB的高，发现对面墙FG上有该房子的影子，小明边移动边观察，发现在点D处竖立一根1.7m长的木棍时，木棍落在墙上的影子与这房子落在墙上的影子重合且高度恰好相同，此时测得墙上影子高EF=1.3m，DF=1m，BF=6m(点B，D，F在同一条直线上)，则房子AB的高为( )
A. 2mB. 2.4mC. 3.7mD. 4.1m
3.在某一时刻，测得一根高为1.8 m的竹竿的影长为3 m，同时测得一根旗杆的影长为25 m，那么这根旗杆的高度为( )
A. 10 mB. 12 mC. 15 mD. 40 m
4.如图，左、右并排的两棵大树的高分别为AB=8m，CD=12m，两树底部的距离BD=5m，王红估计自己眼睛距地面1.6m.她沿着连接这两棵树的一条水平直路l从左向右前进，在前进的过程中，她发现看不到右边较高的树的顶端C，此时，她与左边较低的树AB的水平距离( )
A. 小于8mB. 小于9mC. 大于8mD. 大于9m
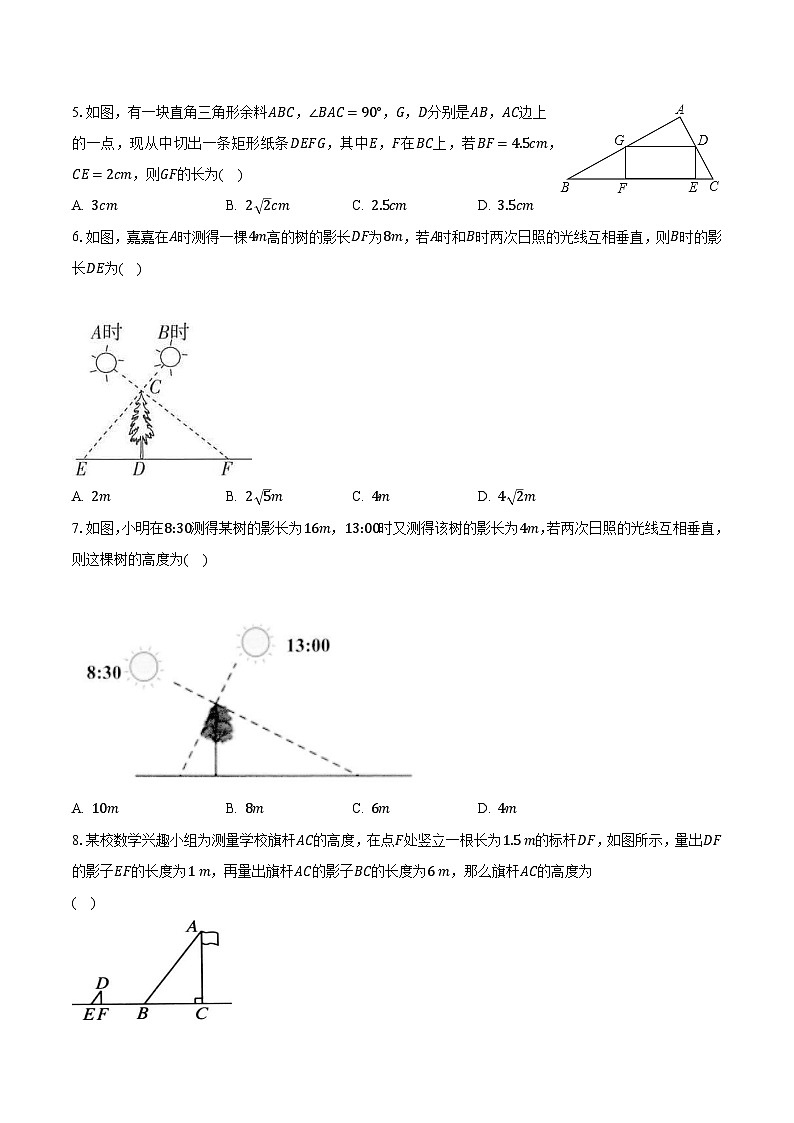
5.如图，有一块直角三角形余料ABC，∠BAC=90°，G，D分别是AB，AC边上的一点，现从中切出一条矩形纸条DEFG，其中E，F在BC上，若BF=4.5cm，CE=2cm，则GF的长为( )
A. 3cmB. 2 2cmC. 2.5cmD. 3.5cm
6.如图，嘉嘉在A时测得一棵4m高的树的影长DF为8m，若A时和B时两次日照的光线互相垂直，则B时的影长DE为( )
A. 2mB. 2 5mC. 4mD. 4 2m
7.如图，小明在8:30测得某树的影长为16m，13:00时又测得该树的影长为4m，若两次日照的光线互相垂直，则这棵树的高度为( )
A. 10mB. 8mC. 6mD. 4m
8.某校数学兴趣小组为测量学校旗杆AC的高度，在点F处竖立一根长为1.5 m的标杆DF，如图所示，量出DF的影子EF的长度为1 m，再量出旗杆AC的影子BC的长度为6 m，那么旗杆AC的高度为
( )
A. 6 mB. 7 mC. 8.5 mD. 9 m
9.如图，小树AB在路灯O的照射下形成投影BC.若树高AB=2m，树影BC=3m，树与路灯的水平距离BP=4.5m.则路灯的高度OP为
( )
A. 3mB. 4mC. 4.5mD. 5m
10.如图，小明在A时测得某树的影长为2m，B时又测得该树的影长为8m，若两次日照的光线互相垂直，则树的高度为________m.( )
A. 2B. 4C. 6D. 8
第II卷（非选择题）
二、填空题（本大题共4小题，共12.0分）
11.如图，为了测量旗杆的高度，某综合实践小组设计了以下方案：用2.5m长的竹竿做测量工具，移动竹竿，保持竹竿与旗杆平行，使竹竿、旗杆的顶端的影子恰好落在地面的同一点．此时，竹竿与这一点相距5m、与旗杆相距20m，则旗杆的高度为___米．
12.我国古代数学著作《九章算术》中记载了一个问题：“今有邑方不知大小，各开中门，出北门三十步有木，出西门七百五十步见木，问：邑方几何？”其大意是：如图，一座正方形城池，A为北门中点，从点A往正北方向走30步到B处有一树木，C为西门中点，从点C往正西方向走750步到D处正好看到B处的树木，则正方形城池的边长为_______步．
13.我国古代数学发展源远流长，成就辉煌．著作《九章算术》中就有“井深几何”问题：“今有井径五尺，不知其深，立五尺木于井上，从木末望水岸，入径四寸，问井深几何？”现在我们可以解释为：如图，矩形BCDE的边BE、CD表示井的直径，A在CB的延长线上，CD=5尺，AB=5尺，AD交BE于F，BF=0.4尺，根据以上条件，可求得井深BC为 尺．
14.如图，某时刻阳光通过窗口AB照射到室内，在地面上留下4米宽的“亮区”DE，光线与地面所成的角(如∠BEC)的正切值是12，那么窗口的高AB等于______米．
三、解答题（本大题共6小题，共48.0分。解答应写出文字说明，证明过程或演算步骤）
15.(本小题8.0分)
如图，小明用自制的直角三角形纸板DEF测量水平地面上树AB的高度，已知两直角边EF：DE=3：4，他调整自己的姿势和三角形纸板的位置，使斜边DF保持水平，并且边DE与点B在同一直线上，DM垂直于地面，测得AM=16m，边DF离地面的距离为1.5m，求树高AB．
16.(本小题8.0分)
如图是位于陕西省西安市荐福寺内的小雁塔，是中国早期方形密檐式砖塔的典型作品，并作为丝绸之路的一处重要遗址点，被列入《世界遗产名录》.小铭、小希等几位同学想利用一些测量工具和所学的几何知识测量小雁塔的高度，由于观测点与小雁塔底部间的距离不易测量，因此经过研究需要进行两次测量，于是在阳光下，他们首先利用影长进行测量，方法如下：小铭在小雁塔的影子顶端D处竖直立一根木棒CD，并测得此时木棒的影长DE=2.4米；然后，小希在BD的延长线上找出一点F，使得A、C、F三点在同一直线上，并测得DF=2.5米．已知图中所有点均在同一平面内，木棒高CD=1.72米，AB⊥BF，CD⊥BF，试根据以上测量数据，求小雁塔的高度AB．
17.(本小题8.0分)
某学习小组为了测量校园内一棵小树AB的高度，用一根长为1米的竹竿CD作为测量工具.将竹竿垂直于地面放置，移动竹竿，使其影子的顶端，小树影子的顶端在水平地面上的同一点E处重合，且B，D，E三点共线.若测得BE长为4.5米，BD长为3米，求这棵小树AB的高度．
18.(本小题8.0分)
小明利用刚学过的测量知识来测量学校内一棵古树的高度．一天下午，他和学习小组的同学带着测量工具来到这棵古树前，由于有围栏保护，他们无法到达古树的底部B，如图所示．于是他们先在古树周围的空地上选择一点D，并在点D处安装了测量器DC，测得古树的顶端A的仰角为45°；再在BD的延长线上确定一点G，使DG=5米，并在G处的地面上水平放置了一个小平面镜，小明沿着BG方向移动，当移动到点F时，他刚好在小平面镜内看到这棵古树的顶端A的像，此时，测得FG=2米，小明眼睛与地面的距离EF=1.6米，测量器的高度CD=0.5米．已知点F、G、D、B在同一水平直线上，且EF、CD、AB均垂直于FB，求这棵古树的高度AB.(小平面镜的大小忽略不计)
19.(本小题8.0分)
我国古代数学著作《九章算术》中记载了一个问题：“今有邑方不知大小，各开中门，出北门三十步有木，出西门七百五十步见木，问：邑方几何？”.其大意是：如图，一座正方形城池，A为北门中点，从点A往正北方向走30步到B出有一树木，C为西门中点，从点C往正西方向走750步到D处正好看到B处的树木，求正方形城池的边长．
20.(本小题8.0分)
在“物体的高度”活动中，某数学兴趣小组的2名同学选择了测量学校里的两棵树的高度.在同一时刻的阳光下，他们分别做了以下工作：
小芳：测得一根长为1米的竹竿的影长为0.8米，甲树的影长为4.08米(如图1)．
小丽：测量的乙树的影子除落在地面上外，还有一部分落在教学楼的第一级台阶上(如图2)，测得此影子长为0.2米，一级台阶高为0.3米，落在地面上的影长为4.4米．
(1)在横线上直接填写甲树的高度为______ 米.
(2)求出乙树的高度(画出示意图)．
答案和解析
1.【答案】C
【解析】【分析】
本题考查了相似三角形的实际应用，读懂题意，得出关系式是解题的关键．
设AB为树高，BC为树在地面上的影子，CD和DE为树在台阶上的影子，如果我们把BC平移到FD的位置，易知四边形FBCD是矩形，然后根据题意即可列出关系式．
【解答】
解：如图，
设AB为树高，BC为树在地面上的影子，CD和DE为树在台阶上的影子．
如果我们把BC平移到FD的位置，易知四边形FBCD是矩形，
因此FD=BC，则EF=FD+DE=4.6米．
设AB=x(x>0)米，则AF=(x−0.3)米．
根据题意，得10.4=x−0.34.6，解得x=11.8．
则树高为11.8米．
故选C．
2.【答案】C
【解析】解：延长AE、BF交于一点H，如图所示：
设FH=xm，由题意可知：DH=(1+x)m，BH=(6+x)m，
∵EF/​/CD/​/AB，
∴△EFH∽△CDH，△EFH∽△ABH，
∴FHDH=EFCD=，FHBH=EFAB，
∴x1+x=1317，
解得：x=134，
经检验x=134是方程的解，
∴FH=134m,BH=374m，
∵FHBH=EFAB，
∴AB=EF⋅BHFH=1.3×374134=3.7m；
故选：C．
延长AE、BF交于一点H，然后根据相似三角形的性质与判定可进行求解．
本题主要考查相似三角形的性质与判定，熟练掌握相似三角形的性质与判定是解题的关键．
3.【答案】C
【解析】【解析】
本题考查了相似的应用，属于基础题．
根据同时同地物高与影长成正比列式计算即可得解．
【解答】
解：设旗杆高度为x米，
由题意得，1.83=x25，
解得：x=15．
故选C．
4.【答案】A
【解析】解：当小红的眼睛的位置到F′时，C，A，F′共线，
∵AB⊥l，CD⊥l，
∴AB/​/CD，
∴△F′AH∽△F′CK，
∴F′H：F′K=AH：CK，
∵AH=AB−BH=8−1.6=6.4(m)，CK=CD−KD=12−1.6=10.4(m)，
∴F′H：(F′H+5)=6.4：10.4，
∴F′H=8(m)，
在前进的过程中，小红发现看不到右边较高的树的顶端C，此时，她与左边较低的树AB的水平距离小于8m．
故选：A．
当小红的眼睛的位置到F′时，C，A，F′共线，此时由△F′AH∽△F′CK得到F′H：F′K=AH：CK，求出F′H即可解决问题．
本题考查相似三角形的应用，关键是从问题中抽象出相似三角形，由相似三角形的性质来解决问题．
5.【答案】A
【解析】解：∵∠BAC=90°，
∴∠AGD+∠ADC=90°，
∵四边形GFDE是矩形，
∴∠GDE=90°，∠GFB=∠DEC=90°，GD/​/BC，GF=DE，
∴∠ADG+∠EDC=90°，∠AGD=∠B，
∴∠AGD=∠EDC，
∴∠B=∠EDC，
∴△BFG∽△DEC，
∴DE：BF=CE：GF，
∵BF=4.5cm，CE=2cm，
∴GF：4.5=2：GF，
∴GF=3cm，
故选：A．
根据题意推知△BFG∽△DEC，由该相似三角形的对应边成比例，求得GF的长度即可．
本题考查了相似三角形的应用和矩形的性质．利用数学知识解决实际问题是中学数学的重要内容．解决此问题的关键在于正确理解题意的基础上建立数学模型，把实际问题转化为数学问题．
6.【答案】A
【解析】由题意得CE⊥CF，CD=4m，FD=8m，∴∠ECF=90∘，∴∠ECD+∠DCF=90∘．∵CD⊥EF，∴∠CDE=∠CDF=90∘，∴∠CFD+∠DCF=90∘，∴∠ECD=∠CFD，∴Rt△CDE∽Rt△FDC，∴EDCD=CDFD，即CD2=ED⋅FD，∴42=8ED，解得ED=2m，即B时的影长DE为2m.故选A．
7.【答案】B
【解析】【分析】
本题考查了相似三角形的判定与性质的应用，属于基础题.根据题意，画出示意图，易得Rt△ECD∽Rt△CFD，进而可得EDDC=DCFD，即DC2=ED·FD，代入数据可得答案．
【解答】
解：根据题意，作△EFC；
树高为CD，且∠ECF=90°，ED=4m，FD=16m；
∵∠E+∠ECD=∠E+∠CFD=90°，
∴∠ECD=∠CFD，
∴Rt△EDC∽Rt△CDF，
∴EDDC=DCFD，
即DC2=ED·FD，
∵ED=4m，DF=16m，
∴DC2=64，
∴DC=8m，(负值舍去)
故选B.
8.【答案】D
【解析】【分析】
本题考查了相似三角形在测量高度时的应用，解题时关键是找出相似的三角形，然后根据对应边成比例列出方程，建立适当的数学模型来解决问题．在同一时刻的两个物体，影子，经过物体顶部的太阳光线三者构成的两个直角三角形相似．根据相似三角形的对应边的比相等，即可求解．
【解答】
解：∵标杆的高标杆的影长=旗杆的高旗杆的影长
即1.51=AC6，
∴AC=6×1.5=9米．
故选D．
9.【答案】D
【解析】【分析】
本题考查中心投影，相似三角形的判定和性质等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．利用相似三角形的性质求解即可．
【解答】
解：∵AB//OP，
∴△CAB∽△COP，
∴CBCP=ABOP，
∴37.5=2OP，
∴OP=5(m)，
故选：D．
10.【答案】B
【解析】【分析】
本题主要考查相似三角形的判定和性质，正确找出相似三角形是解题的关键．
先根据已知条件证明Rt△EDC∽Rt△CDF，列出比例式，即可得出答案．
【解答】
解：如图：过点C作CD⊥EF，
由题意得：△EFC是直角三角形，∠ECF=90°，
∴∠EDC=∠CDF=90°，
∴∠E+∠ECD=∠ECD+∠DCF=90°，
∴∠E=∠DCF，
∴Rt△EDC∽Rt△CDF，
∴EDDC=DCFD；即DC2=ED⋅FD，
代入数据可得DC2=16，
DC=4；
故选B．
11.【答案】12.5
【解析】【分析】
本题考查了相似三角形在测量高度时的应用，解题时关键是找出相似的三角形，然后根据对应边成比例列出比例式，建立适当的数学模型来解决问题．
根据题意，综合实践小组移动竹竿，旗杆、竹竿和影子及经过旗杆和竹竿顶端的光线构成两个直角三角形，且两三角形相似．利用相似三角形对应边成比例解题．
【解答】
解：因为竹竿和旗杆均垂直于地面，
所以构成两个相似三角形，
设旗杆高x米，
则2.5x=55+20，
∴x=12.5．
故答案为12.5．
12.【答案】300
【解析】【分析】
本题考查了相似三角形的应用，解题的关键是构建三角形相似，利用相似比计算对应的线段长．
设正方形城池的边长为x步，则AE=CE=12x，证明Rt△BEA∽Rt△EDC，利用相似比得到3012x=12x750，然后利用比例性质求出x即可．
【解答】
解：设正方形城池的边长为x步，
则AE=CE=12x，
∵AE//CD，∴∠BEA=∠EDC，
∴Rt△BEA∽Rt△EDC，
∴ABEC=AECD，即3012x=12x750，
∴x=300，
即正方形城池的边长为300步．
故答案为300．
13.【答案】57.5
【解析】【分析】
利用相似三角形的判定和性质，构建方程求解即可．
本题考查相似三角形的应用，矩形的性质等知识，解题的关键是学会利用参数构建方程解决问题，属于中考常考题型．
【解答】
解：设BC=x尺．
∵四边形BCDE是矩形，
∴BF//CD，
∴△AFB∽△ADC，
∴FBDC=ABAC，
∴0.45=55+x，
解得x=57.5，
经检验：x=57.5是分式方程的解．
∴BC=57.5(尺)．
故答案为：57.5．
14.【答案】2
【解析】解：由题意知tan∠BEC=BCCE=ACCD=12，DE=4，
∴CE=2BC，CD=2AC，
∴CD=DE+CE=4+2BC，
∵AD/​/BE，
∴△BCE∽△ACD，
∴BCAC=CECD，
∴BCBC+AB=2BC4+2BC=BC2+BC，
∴BC+AB=2+BC，
∴AB=2，
故答案为：2．
由题意知CE=2BC，CD=2AC，进而得到CD=DE+CE=4+2BC，由BE//AD得到△BCE∽△ACD，根据相似三角形的性质得到BCBC+AB=2BC4+2BC=BC2+BC，化简即可求出AB．
本题考查的是相似三角形的应用，熟知相似三角形的对应边成比例是解答此题的关键．
15.【答案】解：∵∠DEF=∠BCD=90°，∠D=∠D
∴△DEF∽△DCB
∴EFDE=BCCD=34，
∵AM=CD=16m，
∴BC=12m，
∴AB=AC+BC
=1.5+12
=13.5(m)．
【解析】本题考查了相似三角形的应用，解题的关键是从实际问题中整理出相似三角形的模型．
利用直角三角形DEF和直角三角形BCD相似，求得BC的长后加上小明同学的身高即可求得树高AB．
16.【答案】解：由题意得，∠ABD=∠CDE=90°，∠ADB=∠CED，
∴△CDE∽△ABD，
∴CDAB=DEBD，
∵∠F=∠F，
∴△CDF∽△ABF，
∴CDAB=DFBF，
∴DEBD=DFBF，
即2.4BD=2.5BD+2.5，
∴BD=60，
∴1.72AB=2.460，
∴AB=43，
答：小雁塔的高度AB是43米．
【解析】根据相似三角形的性质得到CDAB=DEBD，CDAB=DFBF，等量代换得到DEBD=DFBF，代入数据即可得到结论．
本题主要考查了相似三角形的判定与性质，正确得出△AEC∽△ADB是解题关键．
17.【答案】解：由题意得，CD⊥BE，AB⊥BE，DE=BE−BD=1.5米，
∴AB/​/CD，
∴△EDC∽△EBA，
∴ABCD=BEDE，即AB1=4.51.5，
∴AB=3米，
∴这棵小树AB的高度为3米．
【解析】先求出DE=1.5米，然后证明△EDC∽△EBA得到ABCD=BEDE，然后代值计算即可得到答案．
本题主要考查了相似三角形的应用，证明△EDC∽△EBA得到ABCD=BEDE是解题的关键．
18.【答案】解：如图，过点C作CH⊥AB于点H
则CH=BD，BH=CD=0.5 m
在Rt△ACH中，∠ACH=45°
∴AH=CH=BD
∴AB=AH+BH=BD+0.5
∵EF⊥FB，AB⊥FB
∴∠EFG=∠ABG=90°
又∵∠EGF=∠AGB
∴△EFG∽△ABG
∴EFAB=FGBG，即1.6BD+0.5=25+BD
解得BD=17.5
经检验：BD=17.5是原方程的解
∴AB=17.5+0.5=18(m)
∴这棵古树的高AB为18m
【解析】本题考查了相似三角形的应用，过点C作CH⊥AB于点H，则CH=BD，BH=CD=0.5，由等腰直角三角形的性质，得出AH=CH=BD，那么AB=AH+BH=BD+0.5，再证明△EFG∽△ABG，根据相似三角形对应边成比例求出BD=17.5，进而求出AB即可．
19.【答案】解：设正方形城池的边长为x步，
由题意可得，Rt△ABE∽Rt△CED，
∴ABCE=AECD，
即3012x=12x750，
解得，x1=300，x2=−300(不合题意，舍去)，
答：正方形城池的边长为300步．
【解析】根据题意，可知Rt△ABE∽Rt△CED，从而可以得到对应边的比相等，从而可以求得正方形城池的边长．
本题考查相似三角形的应用、数学常识、正方形的性质，解答本题的关键是明确题意．利用相似三角形的性质和数形结合的思想解答．
20.【答案】5.1
【解析】(1)设甲树高x米，根据题意得：
10.8=x4.08，
解得：x=5.1(米)，
故答案为：5.1．
(2)如图，设AB为乙树的高度，EF=0.2米，CE=0.3米，BC=4.4米，
由题意得：DEEF=DE0.2=10.8，BGBC=BG4.4=10.8，
解得DE=0.25，BG=5.5，
∴CD=CE+DE=0.3+0.25=0.55，
∵四边形AGCD是平行四边形，
∴AG=CD=0.55，
则乙树的高度AB=AG+BG=0.55+5.5=6.05(米)．
(1)根据测得一根长为1米的竹竿的影长为0.8米，利用比例式直接得出树高；
(2)根据相似三角形的判定和性质定理，即可求出答案．
此题主要考查了相似三角形的应用，根据同一时刻影长与高成比例以及假设没有墙或台阶时求出影长是解决问题的关键．