青海省西宁市大通县2024届高三上学期开学摸底考试数学（文）试卷(含答案)

这是一份青海省西宁市大通县2024届高三上学期开学摸底考试数学（文）试卷(含答案)，文件包含专题一近代中国人民的反侵略斗争同步练习教师版2023-2024部编版历史八年级上册docx、专题一近代中国人民的反侵略斗争同步练习学生版2023-2024部编版历史八年级上册docx等2份试卷配套教学资源，其中试卷共19页， 欢迎下载使用。


一、选择题
1、设集合,则( )
A.B.C.D.
2、已知,则在复平面内所对应的点位于( )
A.第一象限B.第二象限C.第三象限D.第四象限
3、已知x,y满足约束条件则目标函数的最大值为( )
A.B.C.4D.5
4、乒乓球是中国的国球, 拥有广泛的群众基础, 老少皆宜, 特别适合全民身体段炼. 某小学体育课上, 老师让小李同学从7个乒乓球(其中3只黄色和4只白色) 中随机选取2个,则他选取的乒乓球恰为1黄1白的概率是( )
A.B.C.D.
5、已知为第四象限角,且,则( )
A.B.C.D.
6、在等差数列中,,是方程的两个根,则的前23项的和为( )
A.-184B.-92C.92D.184
7、已知,是两个不重合的平面, 且直线,则“”是“”的( )
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
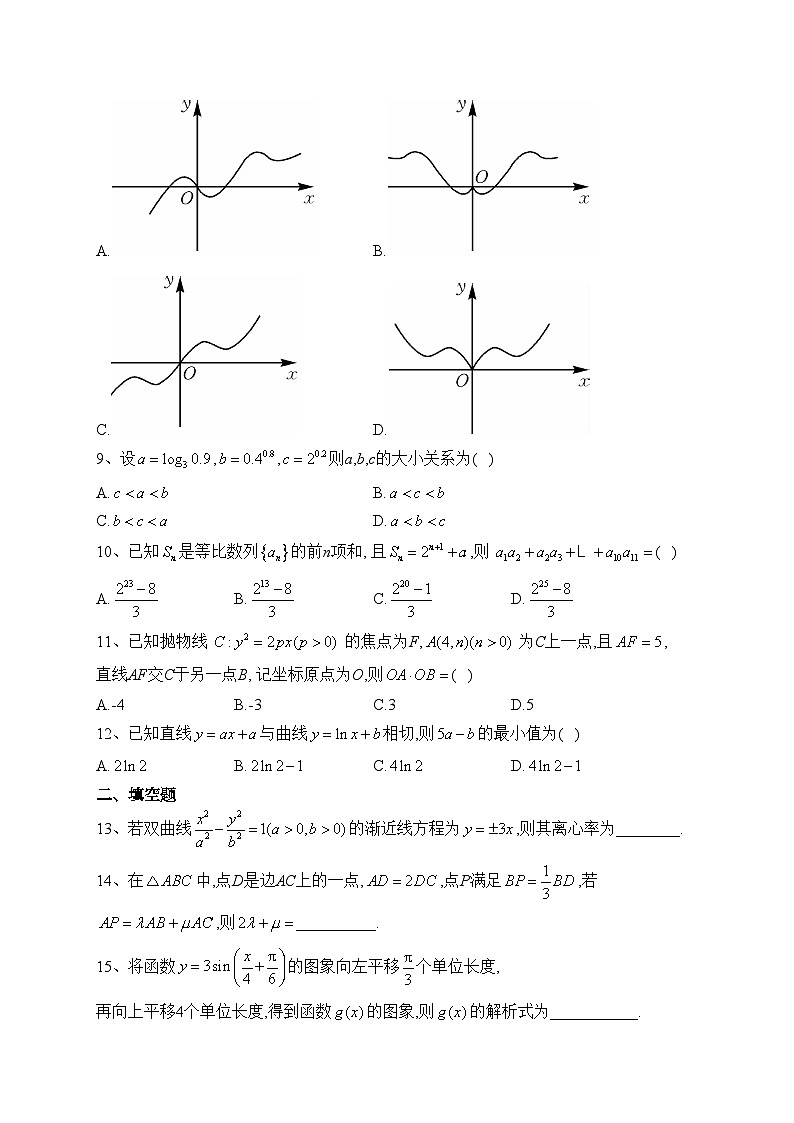
8、函数的图象有可能是( )
A.B.
C.D.
9、设,,则a,b,c的大小关系为( )
A.B.
C.D.
10、已知是等比数列的前n项和, 且,则 ( )
A.B.C.D.
11、已知抛物线 的焦点为F, 为C上一点,且, 直线AF交C于另一点B, 记坐标原点为O,则( )
A.-4B.-3C.3D.5
12、已知直线与曲线相切,则的最小值为( )
A.B.C.D.
二、填空题
13、若双曲线的渐近线方程为,则其离心率为________.
14、在中,点D是边AC上的一点,,点P满足,若,则__________.
15、将函数的图象向左平移个单位长度, 再向上平移4个单位长度,得到函数的图象,则的解析式为___________.
16、某几何体的直观图如图所示，是由一个圆柱体与两个半球对接而成的组合体，其中圆柱体的底面半径为2，高为4.现要加工成一个圆柱，使得圆柱的两个底面的圆周落在半球的球面上，则圆柱的最大体积为___________.
三、解答题
17、如图是M市某爱国主义教育基地宣传栏中标题为“2015-2022年基地接待青少年人次”的统计图.根据该统计图提供的信息解决下列问题.
(1)求M市爱国主义教育基地所统计的8年中接待青少年人次的平均值和中位数;
(2)由统计图可看出,从2019年开始,M市爱国主义教育基地接待青少年的人次呈直线上升趋势,请你用线性回归分析的方法预测2024年基地接待青少年的人次.
①参考公式:对于一组数据,,···其回归直线的斜率和截距的最小二乘法公式分别为,.
②参考数据:
18、记的内角A,B,C的对边分别为a,b,c,,.
(1)求的面积;
(2)若,求b.
19、如图所示,在直三棱柱中,,D,E分别为棱AC,的中点,.
(1)求证:平面;
(2)求多面体的体积.
20、已知椭圆E的中心为坐标原点,对称轴为x轴、y轴,且过,两点.
(1)求E的方程;
(2)若,过的直线l与E交于M,N两点,求证:.
21、已知函数.
(1)讨论的单调性;
(2)若有两个极值点,证明:.
22、在平面直角坐标系xOy中,以O为极点,x轴的正半轴为极轴建立极坐标系,曲线,的极坐标方程分别为,.
(1)求曲线,的直角坐标方程;
(2)若曲线与x轴交于点P,曲线和曲线的交点为A,B,求的值.
23、已知函数.
(1)解不等式;
(2)若的最小值为m,且,求的最小值.
参考答案
1、答案：B
解析：因为,所以.故选B.
2、答案：D
解析：因为,所以,所以在复平面内所对应的点为,位于第四象限.故选D.
3、答案：C
解析：画出满足约束条件的平面区域,如图所示,平移直线,当经过直线与的交点时,目标函数z取得最大值,即.故选C.
4、答案：A
解析：根据古典概型,从7个乒乓球中随机选取2个,基本事件总数有21个,其中恰为1黄1白的基本事件有12个, 所以概率.故选A.
5、答案：C
解析：由题意可知,因为,所以,因为为第四象限角,所以,所以,所以.故选C.
6、答案：C
解析：，是方程的两个根,所以,所以的前23项的和 .故选C.
7、答案：B
解析：若,则,或, 故充分性不成立;因为，是两个不重合的平面,直线,若, 则存在直线, 满足,因为,所以, 所以,故必要性成立.所以“”是 “ ”的必要不充分条件.故选B.
8、答案：A
解析：函数的定义域为R,,可得为奇函数,其图象关于原点对称,可排除选项B、D;的导数为,当时,,单调递减;当时,,单调递增,则在处取得极小值,可排除选项C.故选A.
9、答案：D
解析：因为,，所以.故选D.
10、答案：A
解析：因为,所以,，又是等比数列,所以,即,解得,所以.当 时,,又,所以,所以.故选A.
11、答案：B
解析：由题意得,抛物线的准线为,
因为为C上一点,且,所以,,
解得,故抛物线,焦点为,
所以AF的方程为,代入,得,
整理得,解得或,因为B为C上一点,则,
所以,所以,所以.
故选B.
12、答案：A
解析：设切点为,
则解得
所以
令,所以，
令，解得,令, 解得,
所以在上单调递减,在上单调递增,
所以.故选A.
13、答案：
解析：双曲线的渐近线方程为,即,,离心率.
14、答案：
解析：因为点D是边AC上的一点,,
所以,
所以.
又,所以,所以.
15、答案：
解析：函数的图象向左平移个单位长度,可得，再向上平移 4 个单位长度,可得.
16、答案：
解析：设圆柱的底面半径为r,圆柱的高为,
则,,圆柱的体积,
,可得当时，
, 当时,,则当时,V取得最大值,这时.
17、答案：(1)平均数为:401.25
中位数为:290
(2)1365
解析:(1)平均数为:
,
中位数为:.
(2),,
则,
所以线性回归方程,
所以在2024年时,
所以,
预测2024年基地接待青少年的人次为.
18、答案：(1)
(2)
解析：(1)因为,所以,
所以,
所以,
由正弦定理得,所以,
所以.
又,所以,
,所以.
(2)由正弦定理得: ,
所以,
所以,所以.
19、答案：(1)见解析
(2)
解析：(1)证明:如图, 取的中点F,连接AF,FE,
E是的中点,,.
又,,
,,
四边形ADEF是平行四边形,.
又平面,平面.
平面.
(2)连接,.
平面,平面,.
,且,平面,,
平面.
同理可得平面.
.
20、答案：(1)
(2)见解析
解析：(1)设E的方程为,
过,
所以
解得,
所以E的方程为.
(2)证明:当直线l的斜率为0时,直线l的方程为,
所以,或,.
所以.
当直线l的斜率不为0时,设直线l的方程为,,,
由得,
所以,
,
所以,
所以
所以QP平分,所以.
21、答案：(1)见解析
(2)见解析
解析：(1),
当,即 时,在上恒成立,所以在上单调递增;
当时,令,解得或,令,解得,所以在上单调递增,在上单调递减,在上单调递增;
当时,令,解得,令,解得,
所以在上单调递减,在上单调递增.
(2)证明:,因为有两个极值点,
所以方程有两个根,所以且
解得.
由题意得
.
令,所以,
所以在上单调递减,所以,
即.
22、答案：(1)
(2)10
解析：(1)因为曲线的极坐标方程为,
又,所以,
所以曲线的直角坐标方程为.
因为曲线的极坐标方程为,
所以,
所以曲线的直角坐标方程为.
(2)由题意知,故直线的一个参数方程为(t为参数).
把的参数方程代入,得,
所以,设A,B所对应的参数分别为,
则,所以,同号,
所以.
23、答案：(1)
(2)2
解析:(1)
不等式等价于或或
解得,
故不等式的解集为.
(2)因为,当且仅当时等号成立,所以,
所以,
所以.
因为,当且仅当等号成立,所以,
当且仅当时等号成立,故的最小值为2.
0
1
2
3
-300
-120
90
330