安徽省宿州市2023年八年级上学期期中数学试卷（附答案）

这是一份安徽省宿州市2023年八年级上学期期中数学试卷（附答案），共15页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
1．以下面各组数为边长，不能构成直角三角形的是（ ）
A．3，4，5B．5，12，13
C．，，2D．6，7，8
2．下列实数中，比小的数是（ ）
A．B．C．0D．
3．根据下列表述，能确定位置的是（ ）
A．学校报告厅第三排B．巩义市人民路
C．东经113°，北纬34°D．北偏东30°
4．已知函数是正比例函数，则常数k的值为（ ）
A．-2B．0C．2D．±2
5．下列计算中，正确的是（ ）
A．B．
C．D．
6．如图，小石同学在正方形网格中确定点A的坐标为（﹣1，1），点B的坐标为（2，0），则点C的坐标为（ ）
A．（1，﹣2）B．（﹣2，1）
C．（﹣1，﹣2）D．（1，﹣1）
7．对于一次函数y＝﹣2x+4，下列结论正确的是（ ）
A．函数的图象与y轴的交点坐标是（4，0）
B．函数的图象不经过第三象限
C．函数的图象向上平移4个单位长度得y＝﹣2x的图象
D．若A（x1，y1），B（x2，y2）两点在该函数图象上，且x1＜x2，则y1＜y2
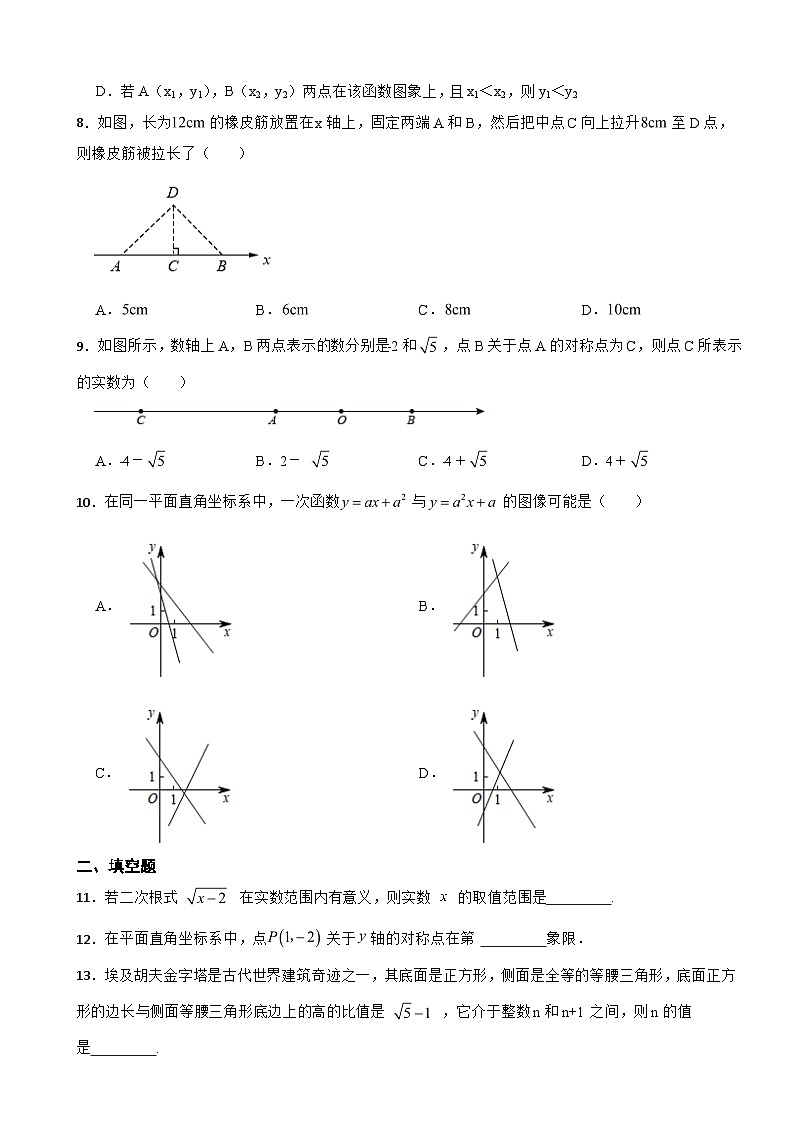
8．如图，长为的橡皮筋放置在x轴上，固定两端A和B，然后把中点C向上拉升至D点，则橡皮筋被拉长了（ ）
A．B．C．D．
9．如图所示，数轴上A，B两点表示的数分别是﹣2和，点B关于点A的对称点为C，则点C所表示的实数为（ ）
A．﹣4－B．2－ C．﹣4＋D．4＋
10．在同一平面直角坐标系中，一次函数与的图像可能是（ ）
A．B．
C．D．
二、填空题
11．若二次根式 在实数范围内有意义，则实数 的取值范围是 .
12．在平面直角坐标系中，点关于轴的对称点在第 象限．
13．埃及胡夫金字塔是古代世界建筑奇迹之一，其底面是正方形，侧面是全等的等腰三角形，底面正方形的边长与侧面等腰三角形底边上的高的比值是 ，它介于整数n和n+1之间，则n的值是 .
14．如图，每个小正方形的边长为1，则∠ABC的度数为 度．
15．如图，杆秤是利用杠杆原理来称物品质量的简易衡器，其秤砣到秤纽的水平距离cm与所挂物重kg之间满足一次函数关系．若不挂重物时秤砣到秤纽的水平距离为cm，挂kg物体时秤砣到秤纽的水平距离为cm．则当秤砣到秤纽的水平距离为cm时，秤钩所挂物重为 ．
16．计算： ．
17．若直角三角形的两条边长为a，b，且满足，则该直角三角形的斜边长为 ．
18．如图，平面直角坐标系中，A（4，4），B为y轴正半轴上一点，连接AB，在第一象限作AC＝AB，∠BAC＝90°，过点C作直线CD⊥x轴于D，直线CD与直线y＝x交于点E，且ED＝5EC，则直线BC解析式为 ．
三、解答题
19．计算：
（1）；
（2）．
20．如图，在平面直角坐标系中，，，．
（1）在图中作出关于轴对称的；
（2）写出点，，的坐标；
（3）求的面积．
21．在中，D是BC上一点，AC=10，CD=6，AD=8，AB=17，求BC的长．
22．小丽根据学习“数与式”积累的经验，想通过“由特殊到一般”的方法探究下面二次根式的运算规律.
下面是小丽的探究过程，请补充完整：
（1）具体运算，发现规律，
特例：
特例：
特例：
特例： 填写一个符合上述运算特征的例子；
（2）观察、归纳，得出猜想.
如果为正整数，用含的式子表示上述的运算规律为： ；
（3）证明你的猜想；
（4）应用运算规律化简： .
23．一条笔直的公路上依次有A、B、C三地，甲车从A地驶往C地，乙车从A地驶往B地，两车同时出发并以各自的速度匀速行驶．乙车中途因汽车故障停下来修理，修好后立却以原速的两倍继续前进到达B地：如图是甲、乙两车与A地的距离y（千米）与出发时间x（小时）之间的大致图象．
（1）求B、C两地之间的距离．
（2）什么时候乙追上甲
（3）当两车相距40千米时，甲车行驶了多长时间？
1．D
2．A
3．C
4．C
5．B
6．A
7．B
8．C
9．A
10．D
11．x≥2
12．三
13．1
14．45
15．5kg
16．
17．2或
18．y＝﹣x+10
19．（1）解：
（2）解：
20．（1）解：如图：
（2）解：由图可知

（3）解：
21．解：∵，
∴，
∵，
∴，
∴，
∴，
∴，
∴．
22．（1）；
（2）；
（3）解：等式左边右边，
故猜想成立
（4）
23．（1）解：（千米），
即B、C两地之间的距离为60千米
（2）解：甲的速度：千米/小时，
乙开始的速度：千米/小时，
乙后来的速度：千米/小时，
由题意得
，
解得，
∴4.5小时后乙追上甲；
（3）解：当时，由题意得
，
解得，不合题意，舍去；
①当时，
设甲距离A地的距离y（千米）与出发时间x（小时）之间的关系式为，
代入可得，
∴，
，解得；
②当时，
由（1）可得，A、B两地之间的距离为：（km），
设乙与A地距离与出发时间x之间的函数关系式为，
代入和，得：
，
解得，
∴，
解方程得（不合题意，舍去），
解方程得；
③当时，
解方程得．
答：当两车相距40千米时，甲车行驶了小时或3.5小时或小时．