吉林省四平市2023年八年级上学期期中数学试题（附答案）

这是一份吉林省四平市2023年八年级上学期期中数学试题（附答案），共15页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
1．已知三角形两边长分别为7、10，那么第三边的长可以是（ ）
A．2B．3C．17D．5
2．n 边形的每个外角都为 15°，则边数 n 为（ ）
A．20B．22C．24D．26
3．如图，要测量湖两岸相对两点A，B的距离，可以在AB的垂线BF上取两点C，D，使CD＝BC，再在BF的垂线DG上取点E，使点A，C，E在一条直线上，可得．判定全等的依据是（ ）
A．B．C．D．
4．已知，如图所示，AD=AC，BD=BC，O为AB上一点，那么，图中共有（ ）对全等三角形．
A．1B．2C．3D．4
5．如图， 中， ， 是 中点，下列结论中错误的是（ ）．
A．B．
C． 平分 D．
6．和点P（﹣3，2）关于x轴对称的点是（ ）
A．（3，2）B．（﹣3，2）
C．（3，﹣2）D．（﹣3，﹣2）
二、填空题
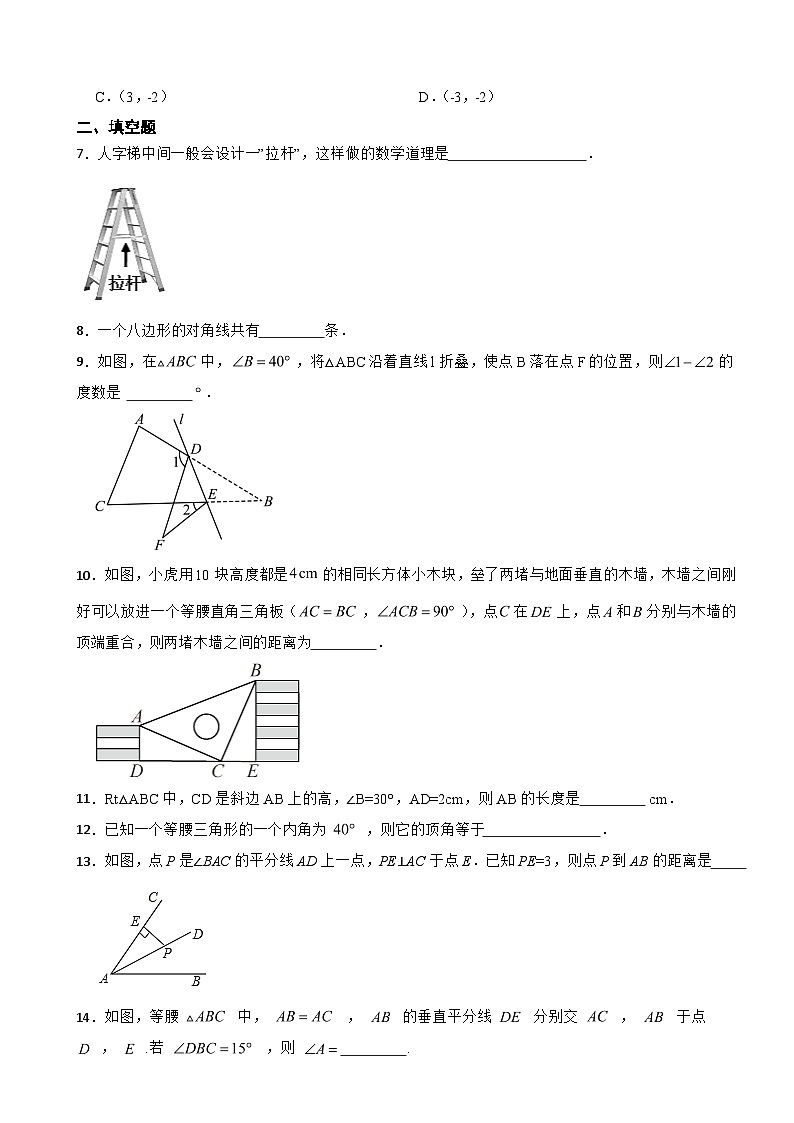
7．人字梯中间一般会设计一”拉杆”，这样做的数学道理是 ．
8．一个八边形的对角线共有 条．
9．如图，在中，，将△ABC沿着直线l折叠，使点B落在点F的位置，则的度数是 ．
10．如图，小虎用10块高度都是的相同长方体小木块，垒了两堵与地面垂直的木墙，木墙之间刚好可以放进一个等腰直角三角板（，），点在上，点和分别与木墙的顶端重合，则两堵木墙之间的距离为 ．
11．Rt△ABC中，CD是斜边AB上的高，∠B=30°，AD=2cm，则AB的长度是 cm．
12．已知一个等腰三角形的一个内角为 ，则它的顶角等于 ．
13．如图，点P是∠BAC的平分线AD上一点，PE⊥AC于点E．已知PE=3，则点P到AB的距离是
14．如图，等腰 中， ， 的垂直平分线 分别交 ， 于点 ， .若 ，则 .
三、解答题
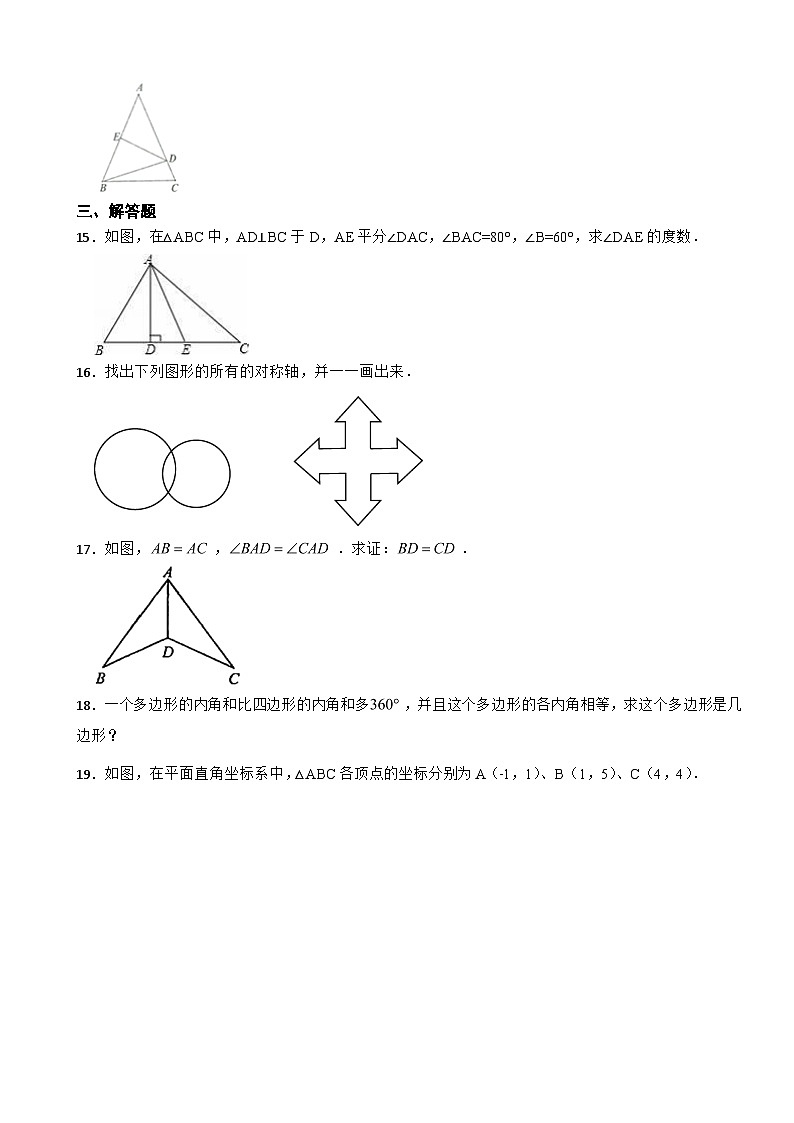
15．如图，在△ABC中，AD⊥BC于D，AE平分∠DAC，∠BAC=80°，∠B=60°，求∠DAE的度数．
16．找出下列图形的所有的对称轴，并一一画出来．
17．如图，，．求证：．
18．一个多边形的内角和比四边形的内角和多，并且这个多边形的各内角相等，求这个多边形是几边形？
19．如图，在平面直角坐标系中，△ABC各顶点的坐标分别为A（﹣1，1）、B（1，5）、C（4，4）．
（1）作出△ABC关于y轴对称的图形△A1B1C1，并写出顶点的坐标．
（2）求△A1B1C1的面积．
20．如图，已知AB=DC，AC=DB．求证：∠1=∠2．
21．如图，中，，于E，F在上，且，，求证：是的平分线．
22．如图，是线段的中点，平分，平分，．
（1）求证：≌；
（2）若=50°，求的度数．
23．如图：已知等边中，D是AC的中点，E是BC延长线上的一点，且，，垂足为M．求证：
（1） ；
（2）M是BE的中点．
24．如图，△ABC 中，AD 是∠BAC 的平分线，DE⊥AB，DF⊥AC，E、F 为垂足，连接 EF 交 AD于G.
（1）求证：AE＝AF.
（2）试判断 AD 与 EF 的位置关系，并说明理由.
25．如图，在中，，，为边的中点，过点A作交的延长线于点平分交于点，为边上一点，连接，且．求证：
（1） ；
（2） ．
26．如图，是等边三角形，，分别是，的中点，连接．
（1）求证：；
（2）在线段的延长线上取点，，使，直线，交于点．
①求证：；
②请判断的形状，并说明理由．
1．D
2．C
3．A
4．C
5．D
6．D
7．三角形的稳定性
8．20
9．80
10．40 cm
11．8
12．40°或100°
13．3
14．50°
15．解：在△ABC中，∵∠BAC+∠B+∠C=180°，
∴∠C=180°﹣80°﹣60°=40°，
∵AD⊥BC于D，
∴∠ADC=90°，在△ADC中，∠DAC=90°﹣∠C=90°﹣40°=50°，
∵AE平分∠DAC，
∴∠DAE= ∠DAC=25°
16．解：所画对称轴如下所示：
17．证明：在和中，，
，
．
18．解：设这个多边形边数为 ，依题意得：
，
解得： ，
答：这个多边形是六边形．
19．（1）解：如图所示：
由图可知，顶点的坐标为（-1，5）；
（2）解：．
20．证明：在△ABC和△DCB中，
，
∴△ABC≌△DCB（SSS），
∴∠1=∠2．
21．证明：在Rt△CDF和Rt△EDB中，，
∴Rt△CDF≌Rt△EDB，
∴DC＝DE，
∵DC⊥AC，DE⊥AB，
∴AD是∠BAC的平分线．
22．（1）解：点 是线段 的中点，
∴ ，
又∵ 平分 ， 平分 ，
∴∠1=∠2，∠2=∠3，
∴∠1=∠3
在 和 中，
∴ ≌
（2）解：∴∠1+∠2+∠3=180°
∴∠1=∠2=∠3=60°
∵ ≌
∴ 50°
∴ ．
23．（1）解：∵三角形ABC是等边△ABC，
∴∠ACB＝∠ABC＝60°，
又∵CE＝CD，
∴∠E＝∠CDE，
又∵∠ACB＝∠E＋∠CDE，
∴∠E＝ ∠ACB＝30°，
∵ ，
∴△EDM是直角三角形，
∴ ；
（2）证明：连接BD，
∵等边△ABC中，D是AC的中点，
∴∠DBC＝ ∠ABC＝ ×60°＝30°
由（1）知∠E＝30°
∴∠DBC＝∠E＝30°
∴DB＝DE
又∵DM⊥BC
∴M是BE的中点．
24．（1）证明：∵△ABC中，∠BAC的平分线交BC于点D，DE⊥AB，DF⊥AC，
∴DF=DE，
在Rt△ADF和Rt△ADE中，
，
∴Rt△ADF≌Rt△ADE，
∴AF=AE
（2）解：AD垂直平分EF；
理由如下：
∵DF=DE，AF=AE，
∴点D在EF的垂直平分线上，点A在EF的垂直平分线上，
∴AD垂直平分EF
25．（1）证明： ， ，
，
平分 ，
，
，
在 与 中，
，
；
（2）证明： 为 边的中点，
，
，
，
，
，
，
，
在 与 中，
，
，
，
由（1）可得： ，
，
．
26．（1）证明： 是等边三角形，
， ，
∵ ， 分别是 ， 的中点，
， ，
，
，
是等边三角形，
，
，
．
（2）①证明： ，
，
在 和 中，
，
；
②解： 是等腰三角形，
理由：∵ ，
∴ ，
，
，
．
即 是等腰三角形．