江西省南昌市2023年八年级上学期期中数学试卷（附答案）

这是一份江西省南昌市2023年八年级上学期期中数学试卷（附答案），共15页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
1．第24届冬奥会于2022年2月4日至20日在北京和张家口举办，北京是全世界唯一同时举办过夏季和冬季奥运会的城市，下列四个图分别是第24届冬奥会部分图标，其中是轴对称图形的为（ ）
A．B．
C．D．
2．如图，在中，，，则的长为（ ）
A．2B．3C．4D．5
3．下列计算正确的是（ ）
A．B．
C．D．
4．如图，已知∠AOB，用直尺、圆规作∠AOB 的角平分线，作法如下：
① 以点O 为圆心，适当长为半径画弧，交OA于点M，交OB 于点N；② 分别以点M，N为圆心，大于 MN 的长为半径画弧，两弧在∠AOB 内部交于点C；③ 画射线OC，OC即为所求．根据上面的作法，可得△OMC≌△ONC，其判定的依据是（ ）
A．SSSB．SASC．ASAD．AAS
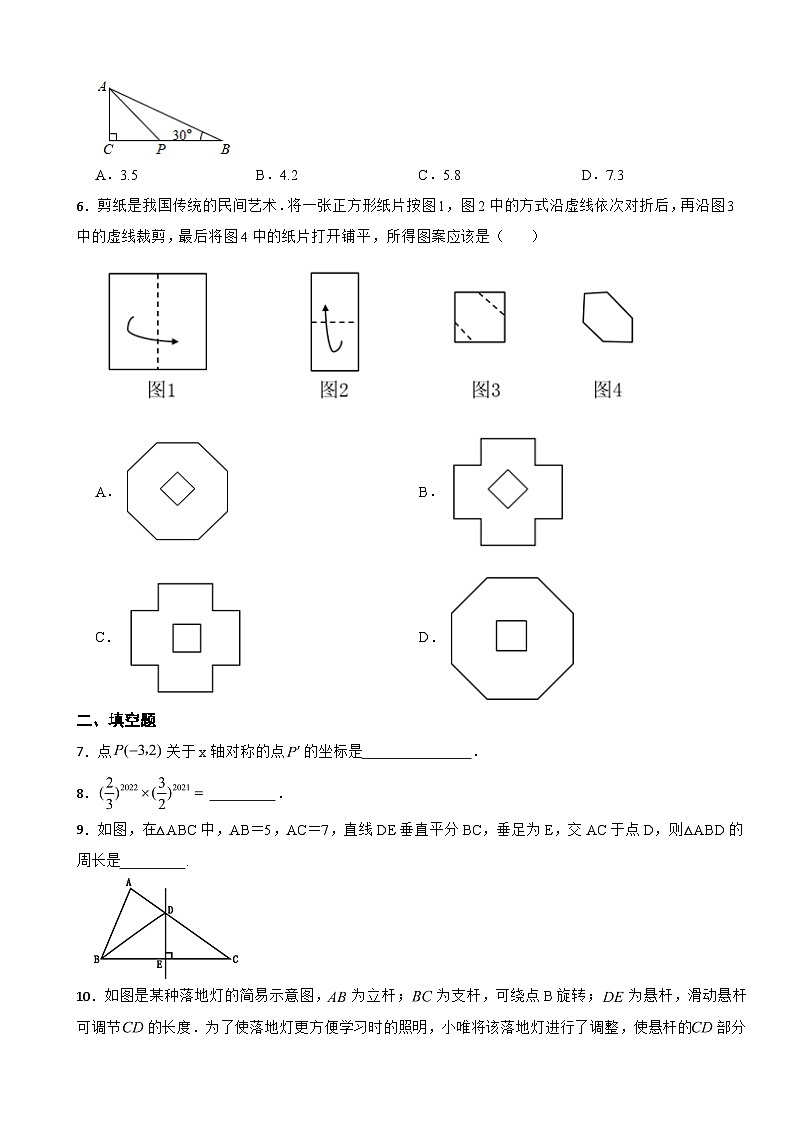
5．如图，△ABC中，∠C＝90°，AB＝8，∠B＝30°，点P是BC边上的动点，则AP长不可能是（ ）
A．3.5B．4.2C．5.8D．7.3
6．剪纸是我国传统的民间艺术．将一张正方形纸片按图1，图2中的方式沿虚线依次对折后，再沿图3中的虚线裁剪，最后将图4中的纸片打开铺平，所得图案应该是（ ）
A．B．
C．D．
二、填空题
7．点关于x轴对称的点的坐标是 ．
8． ．
9．如图，在△ABC中，AB＝5，AC＝7，直线DE垂直平分BC，垂足为E，交AC于点D，则△ABD的周长是 .
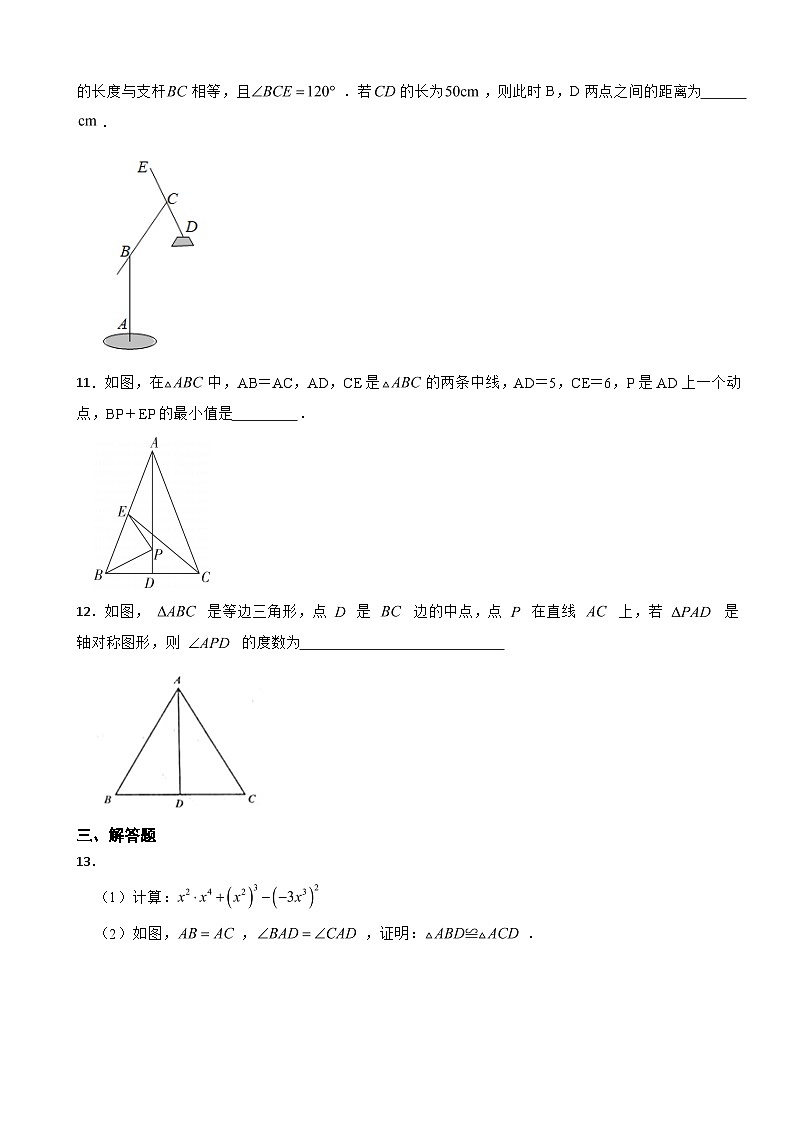
10．如图是某种落地灯的简易示意图，为立杆；为支杆，可绕点B旋转；为悬杆，滑动悬杆可调节的长度．为了使落地灯更方便学习时的照明，小唯将该落地灯进行了调整，使悬杆的部分的长度与支杆相等，且．若的长为，则此时B，D两点之间的距离为 ．
11．如图，在中，AB＝AC，AD，CE是的两条中线，AD＝5，CE＝6，P是AD上一个动点，BP＋EP的最小值是 ．
12．如图， 是等边三角形，点 是 边的中点，点 在直线 上，若 是轴对称图形，则 的度数为
三、解答题
13．
（1）计算：
（2）如图，，，证明：．
14．已知am=2，an=4，求下列各式的值
（1）am+n
（2）a3m+2n．
15．如图，在中，边的垂直平分线相交于点P．
（1）求证；
（2）点P是否也在边的垂直平分线上？由此你还能得出什么结论？
16．如图，在边长为1个单位长度的正方形方格图中，△ABC的顶点都在格点上．按下述要求画图并解答问题：
（1）已知△ABC，直线m，画出△ABC关于直线m对称的图形；分别标出A、B、C三点的对称点D、E、F．
（2）若∠A＝45°，∠B＝64°，求∠F的度数．
17．请仅用无刻度的直尺分别按下列要求画图（保留画图痕迹，不写画法）．
（1）如图1，△ABC中，AB＝AC，点D，E分别在AB，AC边上，且AD＝AE，作出∠BAC的角平分线AF；
（2）如图2，四边形BCED中，BD＝CE，∠B＝∠C，M为BC边上一点，在BC边上作一点N，使CN＝BM．
18．如图，某市有一块长方形地块用来建造住宅、广场和商厦．住宅用地是长为米，宽为米的长方形，广场是长为米，宽为米的长方形．
（1）这块用地的总面积是多少平方米？
（2）求出当时商厦的用地面积．
19．如图，中，，D为上一点，，于点E，于点F，、相交于点G，
（1）求的度数；
（2）求证：．
20．图①中所示的遮阳伞，伞柄垂直于地面，其示意图如图②．当伞收紧时，点P与点A重合；当伞慢慢撑开时，动点P由A向B移动；当点P到过点B时，伞张得最开．已知伞在撑开的过程中，总有PM＝PN＝CM＝CN＝6.0分米，CE＝CF＝18.0分米，BC＝2.0分米．
（1）求AP长的取值范围；
（2）当∠CPN＝60°时，求AP的值．
21．阅读材料：
我们定义：如果两个实数的差等于这两个实数的商，那么这两个实数就叫做“差商等数对”．即：如果，那么α与b就叫做“差商等数对”，记为．例如：；；则称数对，是“差商等数对”．
根据上述材料，解决下列问题：
（1）下列数对中，“差商等数对”是 （填序号）；
①②③
（2）如果是“差商等数对”，请求出a的值；
（3）在（2）的条件下，先化简再求值：．
22．如图，在中，，点D在斜边AB上，，设，．
（1）填写表格：
（2）猜想y与x的数量关系，并说明理由．
（3）在图1的条件下，点E在边上，且，如图2．求的度数．
23．通过对下面数学模型的研究学习，解决下列问题：
（1）【模型呈现】
如图1，，过点B作于点C，过点D作于点E．由，得．又，可以推理得到．进而得到AC＝ ，BC＝ ．我们把这个数学模型称为“K字”模型或“一线三等角”模型；
（2）【模型应用】
①如图2，，连接，且于点F，与直线交于点G．求证：点G是的中点；
②如图3，在平面直角坐标系xOy中，点A的坐标为，点B为平面内任一点．若是以为斜边的等腰直角三角形，请直接写出点B的坐标．
1．D
2．B
3．B
4．A
5．A
6．A
7．（-3，-2）
8．
9．12
10．50
11．6
12．15°或30°或75°或120°
13．（1）解：
=
=
（2）证明：在和中
∴
14．（1）解：∵am=2，an=4，
∴am+n=am×an=2×4=8
（2）解：∵am=2，an=4，
∴a3m+2n=（am）3×（an）2=8×16=128
15．（1）解：∵点P是的垂直平分线上的点，
∴．
同理．
∴．
（2）解：∵PA=PC，
∴点P在边AC的垂直平分线上（和一条线段的两个端点的距离相等的点，在这条线段的垂直平分线上）
还可得出结论：①三角形三边的垂直平分线相交于一点．②这个点与三顶点距离相等．
点P也在边的垂直平分线上，由此可以得出，三角形三条边的垂直平分线相交于一点．
16．（1）解：如图，△DEF即为所求；
（2）解：在△ABC中，∠A=45°，∠B=64°，
∴∠C=180°-∠A-∠B=180°-45°-64°=71°，
∵△ABC与△DEF关于直线m对称，
∴∠F=∠C=71°
17．（1）解：如图所示，AF为∠BAC的角平分线：
（2）解：如图所示，点N即为所求作：
18．（1）解：用地总面积
；
（2）解：商厦的用地面积
．
当时，
原式．
19．（1）解：，，
，
，
，
，
．
（2）证明：，
，
，
，，
，
在和中，
，
，
，
在中，，，
，
．
20．（1）解：∵BC=2分米，AC=CN+PN=12分米，
∴AB=AC﹣BC=10分米．
∴AP的取值范围是：0≤AP≤10；
（2）解：根据题意得CN=PN，∠CPN＝60°，
∴∆CPN为等边三角形，
∴CP=CN=PN=6分米，
∵AC=CN+PN=12分米，
∴AP=AC-CP=6分米．
21．（1）①③
（2）解：由题意得：a−2＝，
解得a＝4；
（3）解：
=
=
=
=
代入a=4，原式=-12．
22．（1）10；20；30
（2）解：猜想：，理由如下：
∵，
∴，
∵，
∴，
∵，
∴；
（3）解：中，，，
∴，
∵，
∴，
∴．
23．（1）DE；AE
（2）解：①如图2，作于M，于N，
∵，
∴，
∵，
∴，
∴，
在与中，，
，
∴（AAS），
∴，
同理，，
∴，
∵，
∴，
在与中，
∴（AAS），
∴，即点G是的中点；
②如图3，和是以为斜边的等腰直角三角形，
过点B作轴于点C，过点A作轴于点E，两直线交于点D，
则四边形为矩形，
∴，
由①可知，，
∴，
∴，
∴，
解得，，
∴点B的坐标为，
同理，点的坐标为，
综上所述，是以为斜边的等腰直角三角形，点B的坐标为或．20
40
60
…



…