山东省菏泽市2023年八年级上学期期中数学试题（附答案）

这是一份山东省菏泽市2023年八年级上学期期中数学试题（附答案），共15页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
1．如图，已知，添加下列一个条件后，仍无法判定的是（ ）
A．B．
C．D．
2．如图下面镜子里哪个是他的像？（ ）
A．B．
C．D．
3．等腰三角形是轴对称图形，它的对称轴是（ ）
A．底边上的高B．底边上的中线
C．顶角的平分线D．底边的垂直平分线
4．如图在中，，若，平分交于点D，且，则点D到线段的距离的长为（ ）
A．4B．8C．10D．12
5．等腰三角形的一边长等于2，另一边长等于5，则其周长为（ ）
A．9B．12C．9或12D．7
6．下列命题中错误的是（ ）
A．全等三角形的对应边相等B．全等三角形的面积相等
C．全等三角形的周长相等D．周长相等的两个三角形全等
7．命题：①对顶角相等；②经过直线外一点，有且只有一条直线与已知直线平行；③相等的角是对顶角；④同位角相等．其中假命题的个数是（ ）
A．1个B．2个C．3个D．4个
8．下列能断定△ABC为等腰三角形的是（ ）
A．∠A=30º、∠B=60ºB．∠A=50º、∠B=80º
C．AB=AC=2，BC=4D．AB=3、BC=7，周长为13
二、填空题
9．如图，若，，，，则的周长为 ．
10．如图，AD为∠BAC的平分线，请你添加一个适当的条件 ，使得．
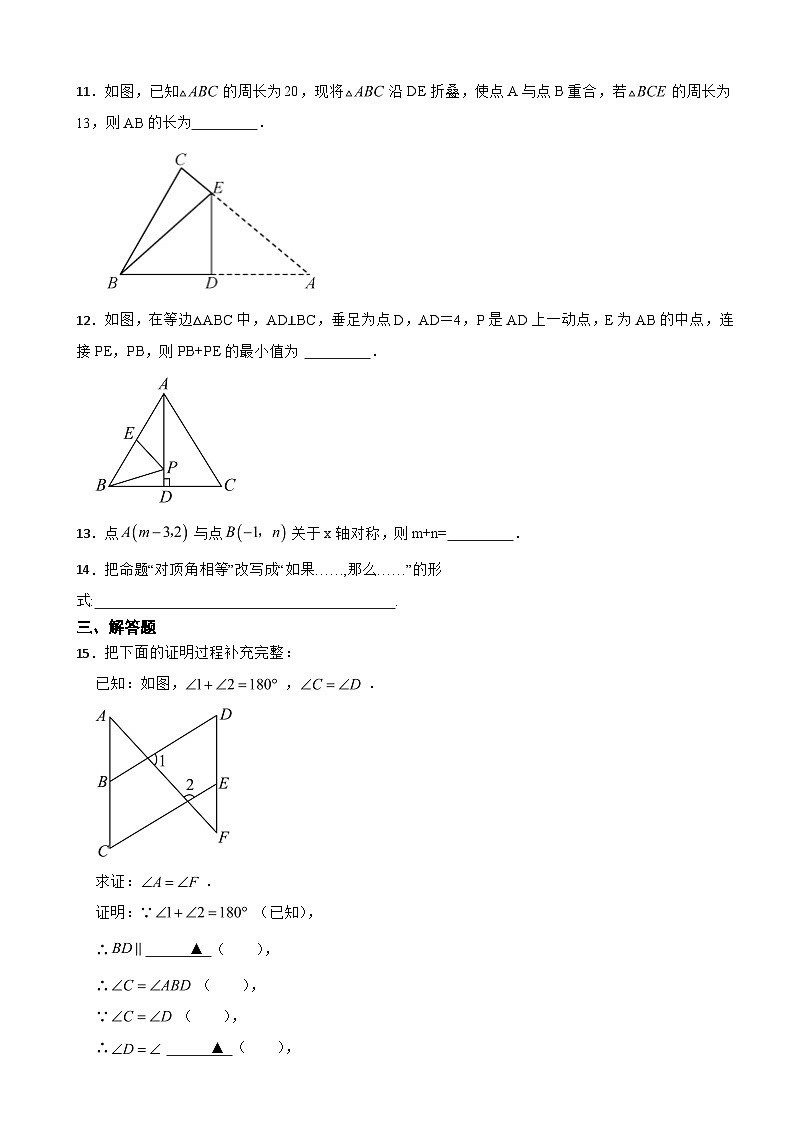
11．如图，已知的周长为20，现将沿DE折叠，使点A与点B重合，若的周长为13，则AB的长为 ．
12．如图，在等边△ABC中，AD⊥BC，垂足为点D，AD＝4，P是AD上一动点，E为AB的中点，连接PE，PB，则PB+PE的最小值为 ．
13．点与点关于x轴对称，则m+n= ．
14．把命题“对顶角相等”改写成“如果……,那么……”的形式: .
三、解答题
15．把下面的证明过程补充完整：
已知：如图，，．
求证：．
证明：∵（已知），
∴ ▲ （ ），
∴（ ），
∵（ ），
∴ ▲ （ ），
∴（ ），
∴（ ）．
16．如图，工人师傅要检查三角形工件ABC的和是否相等，但他手边没有量角器，只有一个刻度尺，他是这样操作的：
①分别在BA和CA上取
②在BC上取
③连接DE、FG，量出DE的长为a米，FG的长为b米．
若，则说明和是相等的，他的这种做法合理吗？为什么？
17．尺规作图：已知△ABC，在△ABC下方作△ABD，使得△ABD≌△ABC（保留作图痕迹，不写作法）．
18．已知命题“如果，那么．”
（1）写出此命题的条件和结论；
（2）写出此命题的逆命题；
（3）判断此命题的逆命题是真命题还是假命题，如果是假命题，请举出一个反例进行说明．
19．如图，等边中，是中点，过作，且，求证：．
20．如图，在中，的垂直平分线交于点E，交于点F，点D为的中点，连接，此时，．求证：．
21．如图，∠B=∠C=90°，E是BC的中点，DE平分∠ADC．求证：AE是∠DAB的平分线．
22．证明：等腰三角形的两底角相等
23．已知，如图，为等边三角形，，AD、BE相交于点P．
（1）求证：；
（2）求证：．
1．B
2．B
3．D
4．B
5．B
6．D
7．B
8．B
9．12
10．AB=AC（答案不唯一）
11．7
12．4
13．0
14．如果两个角是对顶角，那么这两个角相等
15．解：∵（已知），
∴（同旁内角互补两直线平行），
∴（两直线平行同位角相等），
∵（已知），
∴（等量代换），
∴（内错角相等两直线平行），
∴（两直线平行内错角相等）
16．解：这种做法合理．
理由：在和中，
因为，，．
所以．
所以．
17．解：如图，即为所求．
18．（1）解：此命题的条件为：，
结论为：；
（2）解：此命题的逆命题为：如果，那么
（3）解：此命题的逆命题是假命题，
当为相反数时，它们的绝对值相等，但本身不相等，
如时，，而．
19．证明：∵等边三角形ABC中，D是AC中点，
∴AB＝CA，BD是等边三角形ABC的高，
∵AE⊥CE，
∴∠ADB＝∠E=90°，
∵CEAB，
∴∠BAD＝∠ACE，
在△BAD与△ACE中
∵
∴△BAD≌△ACE（AAS）
∴BD＝AE．
20．证明：连接，
∵，，
∴，
∴，
∵点D为的中点，
∴，
∴AD是线段CE的垂直平分线，
∴，
∵EF垂直平分，
∴，
∴．
21．证明：过点E作EF⊥AD，垂足为F．
∵∠B=∠C=90°，
∴BC⊥CD，CB⊥AB．
∵DE平分∠ADC，
∴EC=EF．
∵E为BC的中点，
∴EC=EB，
∴EF=EB，
∵EF⊥AD，CB⊥AB，
∴AE平分∠DAB．
22．证明：已知：△ABC中，AB=AC．
求证：∠B=∠C．
证明：如图，过D作BC⊥AD，垂足为点D，则∠ADB=∠ADC=90°
∵AB=AC，AD=AD
∴Rt△ABD≌Rt△ACD（HL）
∴∠B=∠C.
23．（1）证明：∵为等边三角形，
∴，
∵，
∴
（2）证明：∵，
∴，
∴
．