上海市闵行区2023年八年级上学期期中考试数学试卷（附答案）

这是一份上海市闵行区2023年八年级上学期期中考试数学试卷（附答案），共15页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

1．下列各组二次根式中，属于同类二次根式的是（ ）
A．与B．与
C．与D．与
2．的一个有理化因式是（ ）
A．B．C．D．
3．下列选项中的数是一元二次方程的根的是（ ）
A．B．5C．D．4
4．下列计算正确的是（ ）
A．B．
C．D．
5．下列命题中，假命题的是（ ）
A．在同一平面内，垂直于同一条直线的两条直线平行
B．面积相等的两个三角形全等
C．等腰三角形的顶角平分线垂直于底边
D．三角形的一个外角大于任何一个与它不相邻的内角
6．已知a、b、c是三角形三边的长，则关于x的一元二次方程的实数根的情况是（ ）
A．有两个相等的实数根B．有两个不相等的实数根；
C．没有实数根D．无法确定
二、填空题
7．分母有理化： ．
8．化简：= ．
9．设x是实数，要使得二次根式有意义，x应满足的条件是 ．
10．比较大小： ．（填“>”“<”“=”）
11．已知是关于x的一元二次方程，那么a的取值范围为 ．
12．不等式的解集是 ．
13．方程的根是 ．
14．一种型号的电视，原来每台售价7500元，经过两次降价后，现在每台售价为4800元，如果每次降价的百分率相同，设每次降价百分率为x，那么根据题意可列出方程： ．
15．在实数范围内分解因式： .
16．已知关于x的一元二次方程的一个根是3，则该方程的另一个根是 ．
17．已知：如图，，要使，还需添加一个条件，这个条件可以是 ．写出一个即可）
18．阅读材料：在直角三角形中，斜边和两条直角边满足定理：两条直角边的平方和，等于斜边的平方，因此如果已知两条边的长，根据定理就能求出第三边的长，例如：在中，已知，，，由定理得，代入数据计算求得．
请结合上述材料和已学几何知识解答以下问题：
已知：如图，，，，，，点是的中点，那么的长为 ．
三、解答题
19．
（1）计算：；
（2）计算：（其中）．
20．
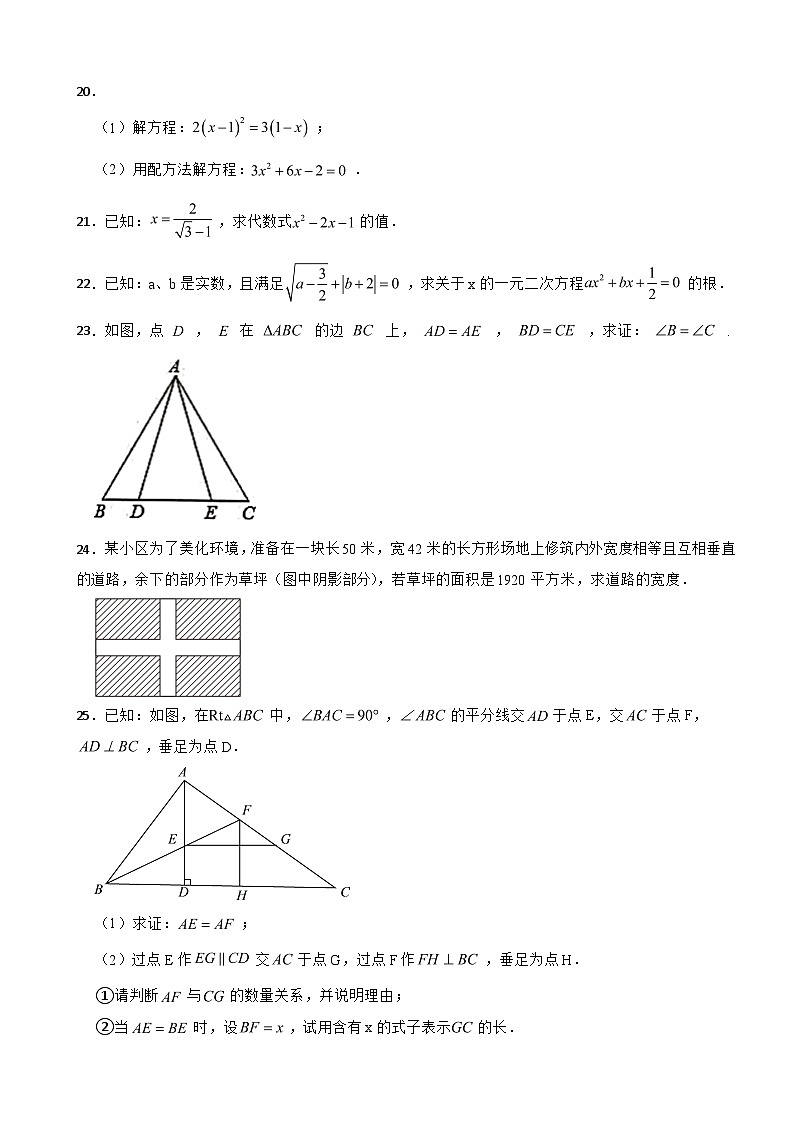
（1）解方程：；
（2）用配方法解方程：．
21．已知：，求代数式的值．
22．已知：a、b是实数，且满足，求关于x的一元二次方程的根．
23．如图，点 ， 在 的边 上， ， ，求证： .
24．某小区为了美化环境，准备在一块长50米，宽42米的长方形场地上修筑内外宽度相等且互相垂直的道路，余下的部分作为草坪（图中阴影部分），若草坪的面积是1920平方米，求道路的宽度．
25．已知：如图，在中，，的平分线交于点E，交于点F，，垂足为点D．
（1）求证：；
（2）过点E作交于点G，过点F作，垂足为点H．
①请判断与的数量关系，并说明理由；
②当时，设，试用含有x的式子表示的长．
1．B
2．A
3．C
4．C
5．B
6．C
7．
8．
9．
10．>
11．
12．
13．，
14．
15．
16．-1
17．BC=BD（答案不唯一）
18．5
19．（1）解：
（2）解：
20．（1）解：
解：移项，得
因式分解得，，
∴或，
解得，；
（2）解：，
解：方程两边同除以，得，
移项，得，
方程两边同加上一次项系数一半的平方，得，
即，
∴，
解得，．
21．解：∵，
∴
．
22．解：∵，，
∴，
∴，
∴原一元二次方程即为，整理得：，
∴，
解得．
23．证明：∵ ，∴ ，
∵ ，
∴ ，
在 和 中，
，
∴ ，
∴ .
24．解：设道路的宽度为x米，
由题意得，
∴，
解得或（不符合题意，舍去）
∴道路的宽度为2米．
25．（1）证明：∵平分，
∴，
∵，
∴，
∴，
∵，
∴，
∴；
（2）解：①，理由如下：
∵平分，，
∴，
由（1）知，
∴，
∵，
∴，，
∴，
∴，
∴；
②∵，
∴，
∵，
∴，
∴，
∴，
∴，
∴．