2023-2024学年广东省广州市荔湾区重点中学高二（上）质检数学试卷（9月份）（含解析）

这是一份2023-2024学年广东省广州市荔湾区重点中学高二（上）质检数学试卷（9月份）（含解析），共7页。试卷主要包含了单选题，多选题，填空题，解答题等内容，欢迎下载使用。
1.已知直线l： 3x+y+3=0，下列结论正确的是( )
A. 直线l的倾斜角为π3B. 直线l的法向量为( 3,−1)
C. 直线l的方向向量为(1, 3)D. 直线l的斜率为− 3
2.若{a,b,c}构成空间的一个基底，则下列向量不共面的是( )
A. b+c，b，b−cB. a，a+b，a−b
C. a+b，a−b，cD. a+b，a+b+c，c
3.关于空间向量，以下说法不正确的是( )
A. 若两个不同平面α，β的法向量分别是u,ν，且n=(1,2,−2),ν=(2,1,2)，则α⊥β
B. 若直线l的方向向量为e=(1,0,3)，平面α的法向量为n=(−2,0,23)，则直线l/​/α
C. 若对空间中任意一点O，有OP=14OA+14OB+12OC，则P，A，B，C四点共面
D. 两个非零向量与任何一个向量都不能构成空间的一个基底，则这两个向量共线
4.如图，在三棱锥O−ABC中，设OA=a，OB=b，OC=c，若AN=NB，BM=2MC，则MN=( )
A. 12a+16b−23c
B. 12a−16b+23c
C. 12a−16b−13c
D. 12a+16b+13c
5.已知△ABC的顶点A(5,5)，AC边上的高所在直线方程为3x+2y−7=0，则AC所在直线的方程为( )
A. x−2y+5=0B. 2x−3y+3=0C. x+2y−15=0D. 2x−3y+5=0
6.如图，在正三棱柱ABC−A1B1C1中，若AB= 2BB1，则AB1与BC1所成角的大小为( )
A. 60°
B. 90°
C. 105°
D. 75°
7.有很多立体图形都体现了数学的对称美，其中半正多面体是由两种或两种以上的正多边形围成的多面体，半正多面体因其最早由阿基米德研究发现，故也被称作阿基米德体.如图，这是一个棱数为24，棱长为 2的半正多面体，它的所有顶点都在同一个正方体的表面上，可以看成是由一个正方体截去八个一样的四面体所得.若点E为线段BC上的动点，则直线DE与直线AF所成角的余弦值的取值范围为( )
A. [13, 22]B. [13, 32]C. [12, 22]D. [12, 32]
8.已知直线l1：kx−y=0过定点A，直线l2：x+ky− 2+2k=0过定点B，l1与l2的交点为C，则|AC|+|BC|的最大值( )
A. 2 6B. 2 5C. 4D. 2 3
二、多选题（本大题共4小题，共20.0分。在每小题有多项符合题目要求）
9.已知空间中三点A0,1,0，B2,2,0，C−1,3,1，则下列说法正确的是
( )
A. AB与AC是共线向量
B. 与AB同向的单位向量是2 55, 55,0
C. AB和BC夹角的余弦值是 5511
D. 平面ABC的一个法向量是1,−2,5
10.已知直线l：x−my+m−1=0，则下列说法正确的是( )
A. 直线l的斜率可以等于0
B. 若直线l与y轴的夹角为30°，则m= 33或m=− 33
C. 直线l恒过点(2,1)
D. 若直线l在两坐标轴上的截距相等，则m=1或m=−1
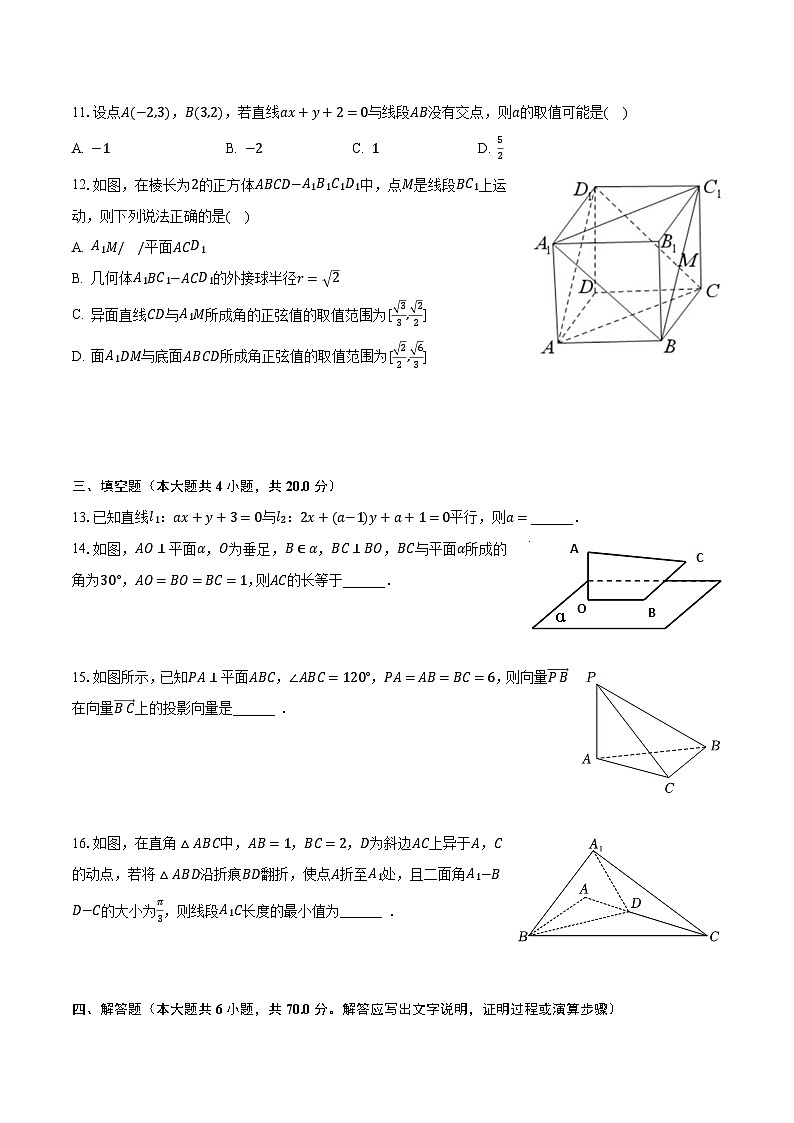
11.设点A(−2,3)，B(3,2)，若直线ax+y+2=0与线段AB没有交点，则a的取值可能是( )
A. −1B. −2C. 1D. 52
12.如图，在棱长为2的正方体ABCD−A1B1C1D1中，点M是线段BC1上运动，则下列说法正确的是( )
A. A1M/​/平面ACD1
B. 几何体A1BC1−ACD1的外接球半径r= 2
C. 异面直线CD与A1M所成角的正弦值的取值范围为[ 33, 22]
D. 面A1DM与底面ABCD所成角正弦值的取值范围为[ 22, 63]
三、填空题（本大题共4小题，共20.0分）
13.已知直线l1：ax+y+3=0与l2：2x+(a−1)y+a+1=0平行，则a=______．
14.如图，AO⊥平面α，O为垂足，B∈α，BC⊥BO，BC与平面α所成的角为30°，AO=BO=BC=1，则AC的长等于______．
15.如图所示，已知PA⊥平面ABC，∠ABC=120°，PA=AB=BC=6，则向量PB在向量BC上的投影向量是______ ．
16.如图，在直角△ABC中，AB=1，BC=2，D为斜边AC上异于A，C的动点，若将△ABD沿折痕BD翻折，使点A折至A1处，且二面角A1−BD−C的大小为π3，则线段A1C长度的最小值为______ ．
四、解答题（本大题共6小题，共70.0分。解答应写出文字说明，证明过程或演算步骤）
17.(本小题10.0分)
如图所示，已知空间四边形ABCD的每条边和对角线长都等于1，点E，F，G分别是AB，AD，CD的中点．设AB=a，AC=b，AD=c．
(1)求证EG⊥AB；
(2)求异面直线AG和CE所成角的余弦值．
18.(本小题12.0分)
求满足下列条件的直线l的一般式方程：
(1)经过直线l1：2x−y+9=0，l2：3x+2y+3=0的交点P，且经过点(2,4)；
(2)与直线l3：3x−y=0垂直，且点Q(2,−5)到直线l的距离为 10．
19.(本小题12.0分)
如图，在棱长为2的正方体ABCD−A1B1C1D1中，E，F分别是AA1，C1D1的中点．
(1)求点B1到平面DEF的距离；
(2)若G是棱AB上一点，当C1G//平面DEF时，求AG的长．
20.(本小题12.0分)
在斜三棱柱ABC−A1B1C1中，△ABC为等腰直角三角形，AB=AC，侧面BB1C1C为菱形，且∠B1BC=60°，点E为棱A1A的中点，EB1=EC，平面B1CE⊥平面BB1C1C.
(1)证明：平面BB1C1C⊥平面ABC；
(2)求二面角E−B1C−A1的余弦值．
21.(本小题12.0分)
如图，将一块直角三角形木板ABO置于平面直角坐标系中，已知AB=OB=1，AB⊥OB，点P(12,14)是三角形木板内一点，现因三角形木板中阴影部分受到损坏，要把损坏部分锯掉，可用经过点P的任一直线MN将三角形木板锯成△AMN，设直线MN的斜率为k．
(1)用k表示出直线MN的方程，并求出M、N的坐标；
(2)求锯成的△AMN的面积的最小值．
22.(本小题12.0分)
如图1，已知ABFE是直角梯形，EF/​/AB，∠ABF=90°，∠BAE=60°，C、D分别为BF、AE的中点，AB=5，EF=1，将直角梯形ABFE沿CD翻折，使得二面角F−DC−B的大小为60°，如图2所示，设N为BC的中点．

(1)证明：FN⊥AD；
(2)若M为AE上一点，且AMAE=λ，则当λ为何值时，直线BM与平面ADE所成角的正弦值为5 714．
答案和解析
1.【答案】D
【解析】解：由题意可得直线的斜率k=− 3，故直线的倾斜角2π3，AC错误，D正确；
与直线l： 3x+y+3=0垂直的直线斜率 33，
所以与l垂直的直线的一个方向向量为(1, 33)，
又( 3,−1)与(1, 33)不平行，B错误．
故选：D．
结合已知直线方程，分别求出直线的斜率，倾斜角及方向向量，法向量，然后检验各选项即可判断．
本题主要考查了直线的斜率，倾斜角及直线的方向向量及法向量的求解，属于基础题．
2.【答案】C
【解析】解：由空间向量基本定理得：
对于A选项，因为b=12(b+c)+12(b−c)，所以b+c，b，b−c三个向量共面，不符合题意；
对于B选项，因为a=12(a+b)+12(a−b)，所以a，a+b，a−b三个向量共面，不符合题意；
对于C选项，假设a+b，a−b，c共面，则c=xa+b+ya−b=x+ya+x−yb，从而可知a，b，c共面，这与已知矛盾，故a+b，a−b，c不共面，符合题意；
对于D选项，a+b+c=(a+b)+(c)，所以三个向量共面，不符合题意；
故选：C．
由空间向量基本定理判断．
本题考查空间向量基本定理以及共面向量定理的应用，属于基础题．
3.【答案】B
【解析】解：对于A，u⋅ν=2+2+(−2)×2=0，所以u⊥ν，A正确；
对于B，e⋅n=−2+0+2=0，所以e⊥n，则直线l/​/α或l⊂α，B错误；
对于C，对空间中任意一点O，有OP=14OA+14OB+12OC，满足14+14+12=1，
则P，A，B，C四点共面，可知C正确；
对于D，两个非零向量与任何一个向量都不能构成空间的一个基底，
则这两个向量共线，所以D正确．
故选：B．
由面面垂直的向量表示可判断A；由线面平行的向量表示可判断B；根据向量共线定理，可判断C；由空间向量基底的表示可判断D．
本题考查面面垂直的向量表示、线面平行的向量表示、向量共线定理、空间向量基底等基础知识，考查运算求解能力，是中档题．
4.【答案】A
【解析】解：MN=MB+BN=23CB+12BA=23(OB−OC)+12(OA−OB)=12OA+16OB−23OC=12a+16b−23c．
故选：A．
根据向量加法、减法和数乘的几何意义，以及向量的数乘运算即可用a,b,c表示出MN．
本题考查了向量加法、减法和数乘的几何意义，向量的数乘运算，考查了计算能力，属于基础题．
5.【答案】D
【解析】解：AC边上的高所在直线方程为3x+2y−7=0，斜率为−32，
则直线AC的斜率为−1−32=23，
∵AC所在直线过顶点A(5,5)，
∴y−5=23(x−5)，即2x−3y+5=0．
故选：D．
根据已知条件，结合直线垂直的性质，以及直线的点斜式公式，即可求解．
本题主要考查直线垂直的性质，以及直线的点斜式公式，属于基础题．
6.【答案】B
【解析】解：在正三棱柱ABC−A1B1C1中，向量BA,BC,BB1不共面，AB1=BB1−BA，BC1=BC+BB1，
令|BB1|=a，则|BA|=|BC|= 2a，而BB1⊥BA,BC⊥BB1，
于是得AB1⋅BC1=(BB1−BA)⋅(BC+BB1)=BB1⋅BC+BB12−BA⋅BC−BA⋅BB1=a2− 2a⋅ 2acs60°=0，
因此，AB1⊥BC1，
所以AB1与BC1所成角的大小为90°．
故选：B．
可得出AB1=BB1−BA，BC1=BC+BB1，并设|BB1|=a，然后即可求出|BA|=|BC|= 2a，并知道BB1⊥BA,BB1⊥BC，然后即可求出AB1⋅BC1的值，从而得出答案．
本题考查了用向量求异面直线所成角的方法，向量加法的平行四边形法则，向量减法的几何意义，向量的数量积的运算，考查了计算能力，属于基础题．
7.【答案】C
【解析】解：如图，
建立如图所示空间直角坐标系，则A(2,1,0)，F(2,2,1)，B(1,0,2)，
C(0,1,2)，D(1,2,2)，设CE=λCB=λ(1,−1,0)=(λ,−λ,0)(0≤λ≤1)，
则DE=DC+CE=(−1,−1,0)+(λ,−λ,0)=(λ−1,−λ−1,0)，
AF=(0,1,1)，
∴cs=DE⋅AF|DE||AF|=−λ−1 2⋅ (λ−1)2+(λ+1)2=−12 1+2λλ2+1=−12 1+2λ+1λ(λ≠0)，
当λ∈(0,1]时，cs∈[− 22,−12)，
当λ=0时，cs=−12，
∴cs∈[− 22,−12]，可得直线DE与直线AF所成角的余弦值的取值范围为[12, 22].
故选：C．
把多面体放入正方体中，建立空间直角坐标系，再由空间向量求解．
本题考查空间中异面直线所成角的求法，考查空间想象能力与思维能力，考查运算求解能力，是中档题．
8.【答案】D
【解析】解：对于直线l1：kx−y=0过定点A(0,0)，
对于直线l2：x+ky− 2+2k=0，即x− 2+k(2+y)=0，
则x− 2=02+y=0，可得x= 2，y=−2，故定点B( 2,−2)，
直线l1：kx−y=0与直线l2：x+ky− 2+2k=0中，
∵k×1+(−1)×k=0，
∴l1⊥l2，
∵l1与l2的交点为C，
∴|CA|2+|CB|2=|AB|2=2+4=6，
∴(|CA|+|CB|2)2=|CA|2+|CB|2+2|CA|⋅|CB|4≤12(|CA|2+|CB|2)=3，
∴|CA|+|CB|2≤ 3，
∴|CA|+|CB|≤2 3，
当且仅当|CA|=|CB|= 3时，|CA|+|CB|的最大值为2 3，
故选：D．
由动直线的方程可得动点A，B的坐标，并且可得两条直线互相垂直，由勾股定理可得|CA|2+|CB|2的值，再由基本不等式可得|AC|+|BC|的最大值．
本题考查的知识要点：直线的方程，定点直线系，主要考查学生的理解能力和计算能力，属于中档题．
9.【答案】BD
【解析】【分析】
利用空面向量坐标运算法则、共线向量、向量夹角公式、法向量直接求解．
本题考查命题真假的判断，考查空面向量坐标运算法则、共线向量、向量夹角公式、法向量等基础知识，考查运算求解能力等数学核心素养，是基础题．
【解答】
解：空间中三点A(0,1,0)，B(2,2,0)，C(−1,3,1)，
对于A，AB=(2,1,0)，AC=(−1,2,1)，
∴AB与AC不是共线向量，故A错误；
对于B，AB=(2,1,0)，AB|AB|=(2 55, 55,0)，故B正确；
对于C，AB=(2,1,0)，BC=(−3,1,1)，
∴AB和BC夹角的余弦值是：
cs=AB⋅BC|AB|⋅|BC|=−5 5⋅ 11=− 5511，故C错误；
对于D，AB=(2,1,0)，AC=(−1,2,1)，
设平面ABC的法向量n=(x,y,z)，
则n⋅AB=2x+y=0n⋅AC=−x+2y+z=0，取x=1，得n=(1,−2,5)，故D正确．
故选：BD．
10.【答案】BD
【解析】【分析】
本题考查直线过定点问题，直线的斜率与倾斜角的关系，直线方程的应用，属于较易题．
根据题意由直线的相关知识，逐个分析即可．
【解答】
解：当m=0时，直线l的斜率不存在，
当m≠0时，直线l的斜率为1m，不可能等于0，故A选项错误；
∵直线l与y轴的夹角为30°，
∴直线l的倾斜角为60°或120°，
∴直线l的斜率为1m，
∴1m=tan60°= 3或1m=tan120°=− 3，
∴m= 33或m=− 33，
故B选项正确；
直线l的方程可化为(x−1)−m(y−1)=0，
所以直线l过定点(1,1)，故C选项错误；
当m=0时，直线l在y轴上的截距不存在，
当m≠0时，令x=0，得y=m−1m，令y=0，得x=1−m，
令m−1m=1−m，得m=±1，故D选项正确，
故选BD．
11.【答案】AC
【解析】解：易知直线ax+y+2=0过定点P(0,−2)，kPA=3−(−2)−2−0=−52，kPB=2−(−2)3−0=43，
直线ax+y+2=0的斜率为−a，由图知−a≥43或−a≤−52，
所以a≤−43或a≥52时有交点，
因此当−43