河南省新乡市获嘉县第一初级中学2023-2024学年八年级上学期10月份月考数学试卷

这是一份河南省新乡市获嘉县第一初级中学2023-2024学年八年级上学期10月份月考数学试卷，共4页。

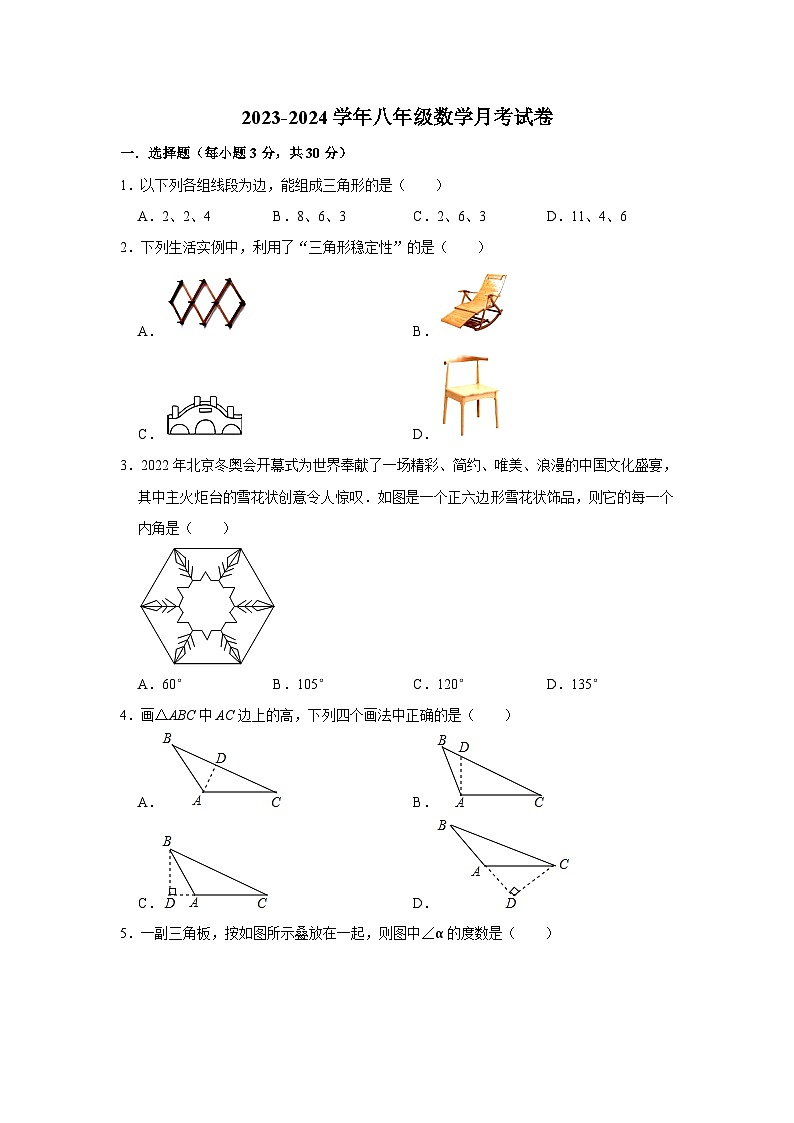
1．以下列各组线段为边，能组成三角形的是（ ）
A．2、2、4B．8、6、3C．2、6、3D．11、4、6
2．下列生活实例中，利用了“三角形稳定性”的是（ ）
A．B．
C．D．
3．2022年北京冬奥会开幕式为世界奉献了一场精彩、简约、唯美、浪漫的中国文化盛宴，其中主火炬台的雪花状创意令人惊叹．如图是一个正六边形雪花状饰品，则它的每一个内角是（ ）
A．60°B．105°C．120°D．135°
4．画△ABC中AC边上的高，下列四个画法中正确的是（ ）
A．B．
C．D．
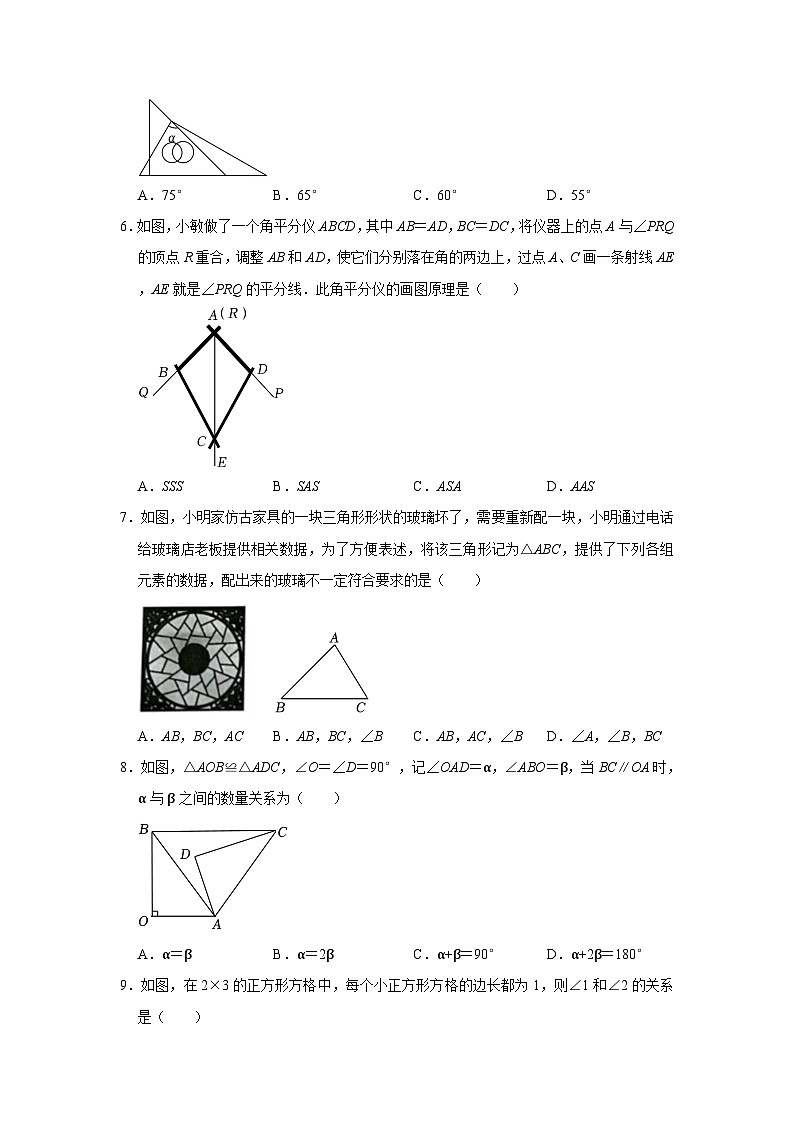
5．一副三角板，按如图所示叠放在一起，则图中∠α的度数是（ ）
A．75°B．65°C．60°D．55°
6．如图，小敏做了一个角平分仪ABCD，其中AB＝AD，BC＝DC，将仪器上的点A与∠PRQ的顶点R重合，调整AB和AD，使它们分别落在角的两边上，过点A、C画一条射线AE，AE就是∠PRQ的平分线．此角平分仪的画图原理是（ ）
A．SSSB．SASC．ASAD．AAS
7．如图，小明家仿古家具的一块三角形形状的玻璃坏了，需要重新配一块，小明通过电话给玻璃店老板提供相关数据，为了方便表述，将该三角形记为△ABC，提供了下列各组元素的数据，配出来的玻璃不一定符合要求的是（ ）
A．AB，BC，ACB．AB，BC，∠BC．AB，AC，∠BD．∠A，∠B，BC
8．如图，△AOB≌△ADC，∠O＝∠D＝90°，记∠OAD＝α，∠ABO＝β，当BC∥OA时，α与β之间的数量关系为（ ）
A．α＝βB．α＝2βC．α+β＝90°D．α+2β＝180°
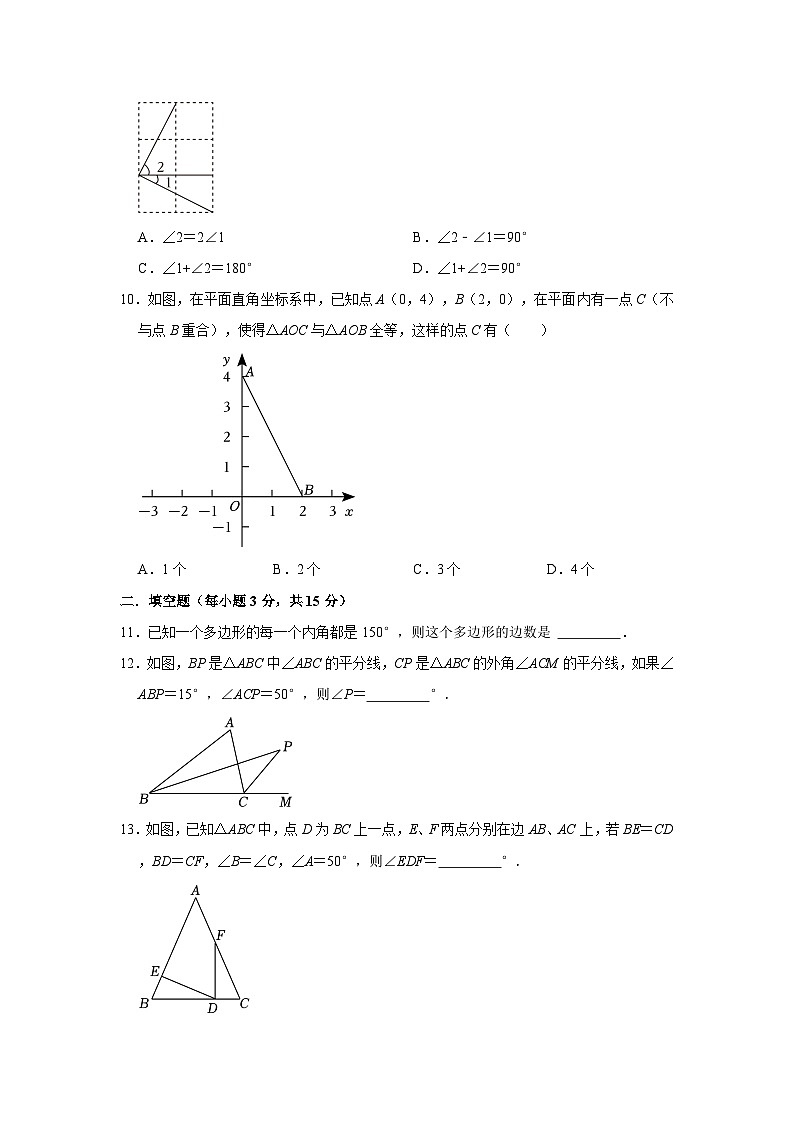
9．如图，在2×3的正方形方格中，每个小正方形方格的边长都为1，则∠1和∠2的关系是（ ）
A．∠2＝2∠1B．∠2﹣∠1＝90°
C．∠1+∠2＝180°D．∠1+∠2＝90°
10．如图，在平面直角坐标系中，已知点A（0，4），B（2，0），在平面内有一点C（不与点B重合），使得△AOC与△AOB全等，这样的点C有（ ）
A．1个B．2个C．3个D．4个
二．填空题（每小题3分，共15分）
11．已知一个多边形的每一个内角都是150°，则这个多边形的边数是 ．
12．如图，BP是△ABC中∠ABC的平分线，CP是△ABC的外角∠ACM的平分线，如果∠ABP＝15°，∠ACP＝50°，则∠P＝ °．
13．如图，已知△ABC中，点D为BC上一点，E、F两点分别在边AB、AC上，若BE＝CD，BD＝CF，∠B＝∠C，∠A＝50°，则∠EDF＝ °．
14．如图所示，若∠A+∠B+∠C+∠D+∠E+∠F＝620°，则∠G+∠H＝ ．
15．如图所示，已知△ABC的周长是20，OB，OC分别平分∠ABC和∠ACB，OD⊥BC于D，且OD＝3，则△ABC的面积是 ．
三．解答题（共8小题，共75分）
16．（9分）如图，在△ABC中，BE是△ABC角平分线，点D是AB上的一点，且满足∠DEB＝∠DBE．
（1）DE与BC平行吗？请说明理由；
（2）若∠C＝50°，∠A＝45°，求∠DEB的度数．
17．（9分）如图，AB∥EF，AC∥DE，FC＝DB，求证：AB＝EF．
18．（9分）如图，在△ABC中，AD是BC边上的高，AE是∠BAC的角平分线．
（1）若∠B＝50°，∠C＝70°求∠EAD的度数；
（2）若∠B=，∠C=，则∠EAD的度数是多少？（用含，的式子表示）．
19．（9分）如图，小刚站在河边的点A处，在河对面（小刚的正北方向）的点B处有一电线塔，他想知道电线塔离他有多远，于是他向正西方向走了30步到达一棵树C处，接着再向前走了30步到达D处，然后他左转90°直行，从点D处开始计步，当小刚看到电线塔、树与自己现处的位置E在一条直线时，他恰好走了80步，并且小刚一步大约0.5米．由此小刚估计出了在点A处时他与电线塔的距离，请问他的做法是否合理？若合理，请求出在点A处时他与电线塔的距离；若不合理，请说明理由．
20．（9分）如图，在△ABC中，AD平分∠BAC，∠C＝90°，DE⊥AB于E，BD＝DF，求证：CF＝EB．
21．（9分）如图，在△ABC中，CD⊥BD，垂足为D，且CD＝BD．BE平分∠ABC，且BE⊥AC，垂足为E，交CD于点F．
（1）求证：AE＝CE；
（2）求证：BF＝2CE．
22．（10分）定义：如果一个三角形的两个内角α与β满足2α+β＝90°，那么我们称这样的三角形为“准互余三角形”．
（1）若△ABC是“准互余三角形”，∠C＞90°，∠A＝60°，则∠B的度数是 ；
（2）若△ABC是直角三角形，∠ACB＝90°．
①如图，若AD是∠BAC的平分线，请判断△ABD是否为“准互余三角形”？并说明理由．
②点E是边BC上一点，△ABE是“准互余三角形”，若∠ABC＝24°，则∠EAC的度数是 ．
23．（11分）在△ABC中，AB＝AC，点D是射线CB上一动点（不与点B，C重合），以AD为一边在AD的右侧作△ADE，使AD＝AE，∠DAE＝∠BAC，连接CE．
（1）如图1，当点D在线段CB上时，BD与CE有何数量关系，请说明理由．
（2）在（1）的条件下，当∠BAC＝90°时，那么∠DCE＝ 度．
（3）设∠BAC＝α，∠DCE＝β．
①如图2，当点D在线段CB上，∠BAC≠90°时，请探究α与β之间的数量关系．并证明你的结论；
②如图3，当点D在线段CB的延长线上，∠BAC≠90°时，请将图3补充完整并直接写出此时α与β之间的数量关系．
2023-2024学年八年级数学月考试卷
参考答案与试题解析
一．选择题（每小题3分，共30分）
1．B．2．B．3．C．4．C．5．A．6．A．7．C．8．B．9．D．10．C．
二．填空题（每小题3分，共15分）
11．12．12．35．13．65．14．100°．15．30．
三．解答题（共8小题，共75分）
16．（9分）解：（1）DE∥BC．
理由如下：∵BE是△ABC的角平分线，
∴∠DBE＝∠EBC，
∵∠DEB＝∠DBE，
∴∠DEB＝∠EBC，
∴DE∥BC；
（2）在△ABC中，∠A+∠ABC+∠C＝180°，
∴∠ABC＝180°﹣∠A﹣∠C＝180°﹣45°﹣50°＝85°．
∵BE是△ABC的角平分线，
∴∠DBE＝∠EBC＝42.5°，
∴∠DEB＝∠EBC＝42.5°．
17．（9分）证明：∵AB∥EF，
∴∠B＝∠F，
∵AC∥DE，
∴∠ACB＝∠EDF，
∵FC＝DB，
∴FC+CD＝DB+CD，
∴FD＝BC，
在△ABC和△EFD中，
，
∴△ABC≌△EFD（ASA），
∴AB＝EF．
18．（9分）
解：（1）∵∠B＝50°，∠C＝70°，
∴∠BAC＝120°，
∵AE是∠BAC的角平分线，
∴∠EAC＝60°，
∵AD⊥BC，∠C＝70°，
∴∠DAC＝20°，
∴∠EAD＝10°，
（2）∵∠BAC＝180°﹣∠C﹣∠B，AE是∠BAC的角平分线，
∴∠EAC＝，
∵AD⊥BC，
∴∠DAC＝90°﹣∠C，
∴∠EAD＝﹣（90°﹣∠C）＝．∵∠B=，∠C=，
∴∠EAD＝.
19．（9分）解：合理．理由如下：
根据题意，得AC＝DC．
在△ABC和△DEC中，
，
∴△ABC≌△DEC（ASA）．
∴AB＝DE．
又∵小刚走完DE用了80步，一步大约0.5米，
∴AB＝DE＝80×0.5＝40（米）．
答：小刚在点A处时他与电线塔的距离为40米．
20．（9分）证明：∵AD平分∠BAC，∠C＝90°，DE⊥AB于E，
∴DE＝DC．
在△CDF与△EDB中，
，
∴Rt△CDF≌Rt△EDB（HL），
∴CF＝EB．
21．（9分）证明：（1）∵BE⊥AC，
∴∠BEC＝∠BEA＝90°，
∵BE平分∠ABC，
∴∠EBC＝∠EBA，
在△CBE和△ABE中，
，
∴△CBE≌△ABE（ASA），
∴AE＝CE；
（2）∵BE⊥AC，CD⊥AB，
∴∠CDA＝∠CDB＝∠BEA＝90°，
∴∠EBA+∠A＝90°，∠ACD+∠A＝90°，
∴∠EBA＝∠ACD，
在△BDF和△CDA中，
，
∴△BDF≌△CDA（ASA ），
∴BF＝AC，
∵AE＝CE，
∴BF＝AC＝2CE．
22．（10分）解：（1）∵△ABC是“准互余三角形”，∠C＞90°，∠A＝60°，
∴∠A+2∠B＝90°，
∴∠B＝15°，
故答案为：15°；
（2）①△ABD是“准互余三角形”，
理由：∵AD是∠BAC的平分线，
∴∠BAC＝2∠BAD，
∵∠ACB＝90°，
∴∠BAC+∠B＝90°，
∴2∠BAD+∠B＝90°，
∴△ABD是“准互余三角形”，
②∵△ABE是“准互余三角形”
∴2∠EAB+∠ABC＝90°或∠EAB+2∠ABC＝90°，
∵∠ABC＝24°，
∴∠EAB＝42°或∠EAB＝33°，
当∠EAB＝42°，∠ABC＝24°时，∠AEB＝114°，
∴∠EAC＝90°﹣∠ABC﹣∠BAE＝24°
当∠EAB＝33°，∠ABC＝24°时，∠AEB＝123°，
∴∠EAC＝90°﹣∠ABC﹣∠BAE＝33°，
∴∠EAC＝33°或24°．
故答案为：33°或24°．
23．（11分）解：（1）BD＝CE，理由：
∵∠BAD+∠DAC＝90°，∠DAC+∠CAE＝90°，
∴∠BAD＝∠CAE，
在△BAD和△CAE中，
，
∴△BAD≌△CAE（SAS），
∴BD＝CE；
（2）∵△BAD≌△CAE，
∴∠ACE＝∠B，
∵∠B+∠ACB＝90°，
∴∠DCE＝∠ACE+∠ACB＝90°；
故答案为：90；
（3）①∵∠BAD+∠DAC＝α，∠DAC+∠CAE＝α，
∴∠BAD＝∠CAE，
在△BAD和△CAE中，
，
∴△BAD≌△CAE（SAS），
∴∠ACE＝∠B，
∵∠B+∠ACB＝180°﹣α，
∴∠DCE＝∠ACE+∠ACB＝180°﹣α＝β，
∴α+β＝180°；
②作出图形，
∵∠BAD+∠BAE＝α，∠BAE+∠CAE＝α，
∴∠BAD＝∠CAE，
在△BAD和△CAE中，
，
∴△BAD≌△CAE（SAS），
∴∠AEC＝∠ADB，
∵∠ADE+∠AED+α＝180°，∠CDE+∠CED+β＝180°，
∠CED＝∠AEC+∠AED，
∴α＝β．
声明：试题解析著作权属所有，未经书面同意，不得复制发布日期：2023/11/1 11:04:14；用户：627273352；邮箱：627273352@qq.cm；学号：4633110