第02讲 三角恒等变换（和差公式、倍角公式）（5类核心考点精讲精练）-备战2024年高考数学一轮复习（新教材新高考）

这是一份第02讲 三角恒等变换（和差公式、倍角公式）（5类核心考点精讲精练）-备战2024年高考数学一轮复习（新教材新高考），共27页。试卷主要包含了 4年真题考点分布， 命题规律及备考策略等内容，欢迎下载使用。
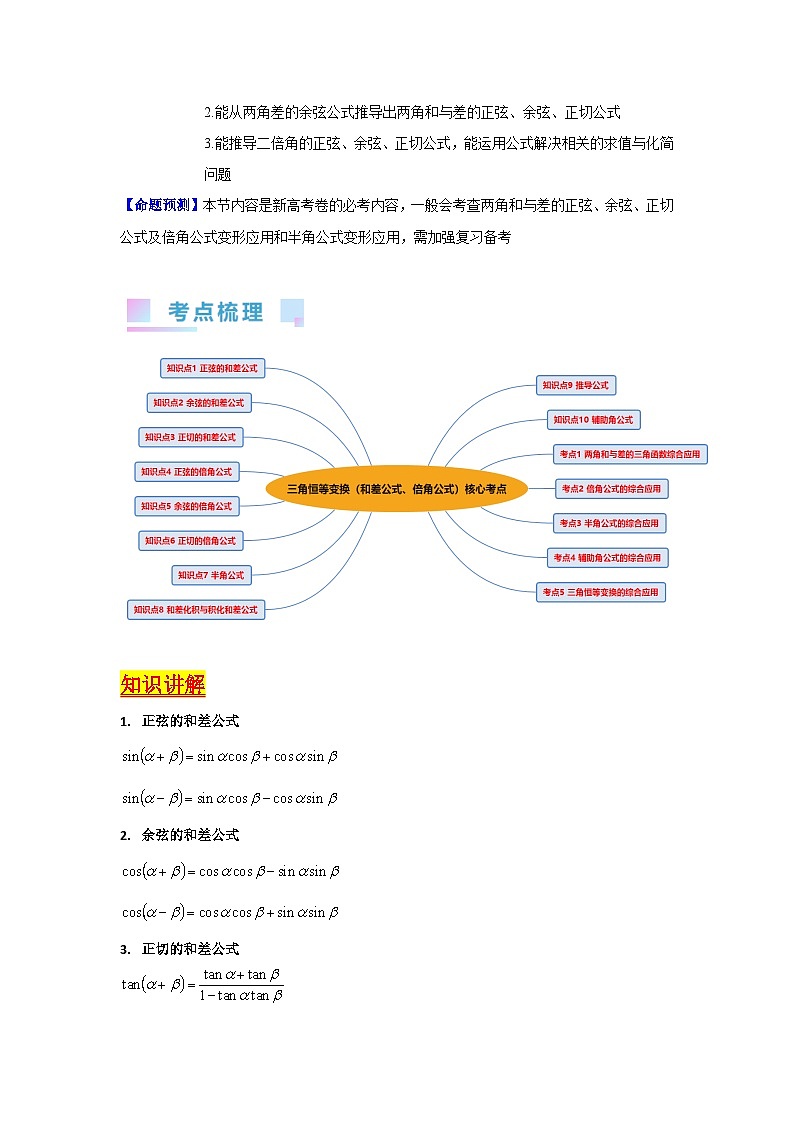
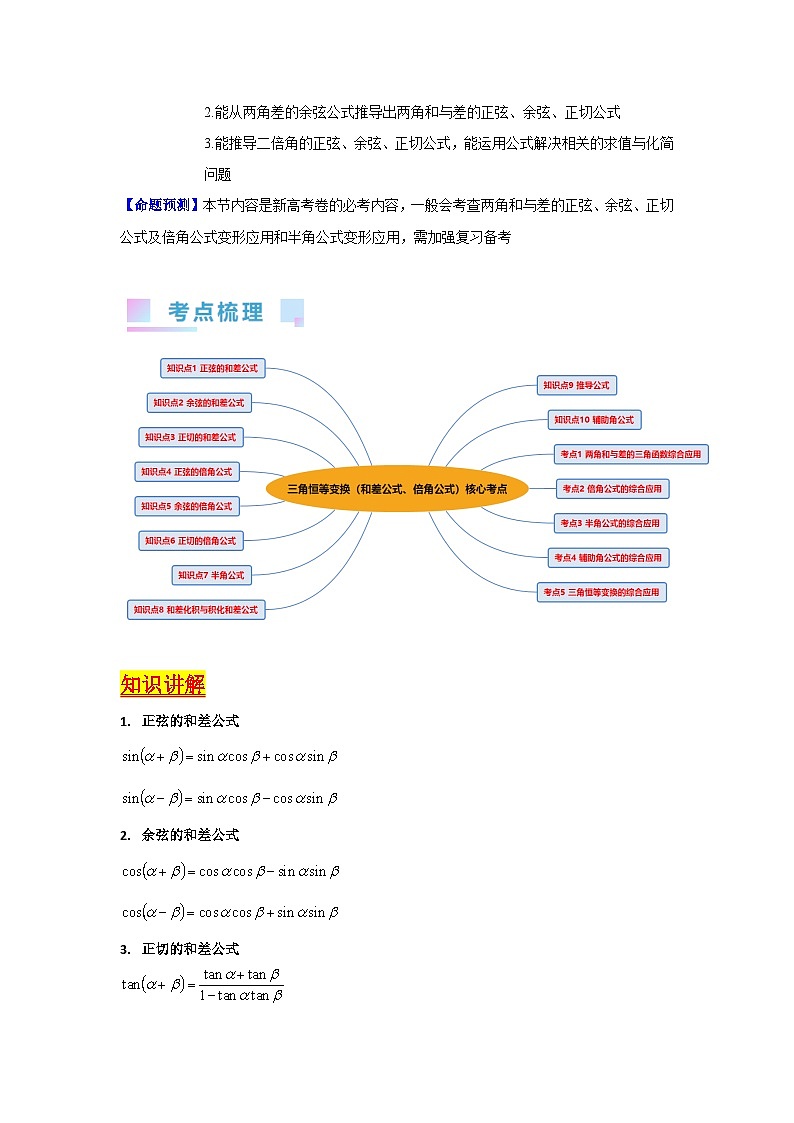
（核心考点精讲精练）
1. 4年真题考点分布
2. 命题规律及备考策略
【命题规律】本节内容是新高考卷的必考内容，设题稳定，难度较中等或偏难，分值为5分
【备考策略】1.推导两角差余弦公式，理解两角差余弦公式的意义
2.能从两角差的余弦公式推导出两角和与差的正弦、余弦、正切公式
3.能推导二倍角的正弦、余弦、正切公式，能运用公式解决相关的求值与化简问题
【命题预测】本节内容是新高考卷的必考内容，一般会考查两角和与差的正弦、余弦、正切公式及倍角公式变形应用和半角公式变形应用，需加强复习备考
知识讲解
正弦的和差公式
余弦的和差公式
正切的和差公式
正弦的倍角公式
余弦的倍角公式
升幂公式：
，
降幂公式：
，
正切的倍角公式
半角公式
(1)sin eq \f(α,2)＝± eq \r(\f(1－cs α,2)).
(2)cseq \f(α,2)＝± eq \r(\f(1＋cs α,2)).
(3)taneq \f(α,2)＝± eq \r(\f(1－cs α,1＋cs α))＝eq \f(sin α,1＋cs α)＝eq \f(1－cs α,sin α).
以上称之为半角公式，符号由eq \f(α,2)所在象限决定．
和差化积与积化和差公式
推导公式
辅助角公式
，，其中，
考点一、两角和与差的三角函数综合应用
1．（福建·高考真题）等于（ ）
A．0B．C．1D．
2．（江西·高考真题）若tanα＝3，tanβ＝，则tan(α－β)等于（ ）
A．3B．－3C．D．
3．（2022·全国·统考高考真题）若，则（ ）
A．B．
C．D．
4．（2020·全国·统考高考真题）已知，则（ ）
A．B．C．D．
1．（2023·全国·高三专题练习）（ ）
A．B．C．D．
2．（2023·云南昭通·统考模拟预测）的值为（ ）
A．B．1C．D．
3．（2020·全国·统考高考真题）已知2tanθ–tan(θ+)=7，则tanθ=（ ）
A．–2B．–1C．1D．2
4．（2023·福建厦门·统考模拟预测）已知，则（ ）
A．0B．C．D．
5．（2004·上海·高考真题）若，则 .
6．（2023·山东德州·三模）若为锐角，且，则 ．
考点二、倍角公式的综合应用
1．（2021·全国·统考高考真题）（ ）
A．B．C．D．
2．（2020·江苏·统考高考真题）已知 =，则的值是 .
3．（2021·全国·统考高考真题）若，则（ ）
A．B．C．D．
4．（2023·全国·统考高考真题）已知，则（ ）．
A．B．C．D．
5．（2021·全国·高考真题）若，则（ ）
A．B．C．D．
1．（2021·北京·统考高考真题）函数是
A．奇函数，且最大值为2B．偶函数，且最大值为2
C．奇函数，且最大值为D．偶函数，且最大值为
2．（2023·山东泰安·统考模拟预测）已知，则（ ）
A．B．C．D．
3．（2023·湖南·校联考二模）已知，则（ ）
A．B．C．D．
4．（2022·浙江·统考高考真题）若，则 ， ．
5．（2020·浙江·统考高考真题）已知，则 ； ．
考点三、半角公式的综合应用
1．（2023·全国·统考高考真题）已知为锐角，，则（ ）．
A．B．C．D．
2．（全国·高考真题）已知，求的值．
1．（2023·四川泸州·统考模拟预测）已知，若是第二象限角，则（ ）
A．B．C．D．
2．（2023·江西·校联考模拟预测）若，是第三象限的角，则＝（ ）
A．2B．C．﹣2D．
3．（2023·浙江·校联考二模）数学里有一种证明方法叫做Prfwithutwrds，也被称为无字证明，是指仅用图象而无需文字解释就能不证自明的数学命题，由于这种证明方法的特殊性，无字证时被认为比严格的数学证明更为优雅与有条理.如下图，点为半圆上一点，，垂足为，记，则由可以直接证明的三角函数公式是（ ）
A．B．
C．D．
考点四、辅助角公式的综合应用
1．（2022·北京·统考高考真题）若函数的一个零点为，则 ； ．
2．（2021·全国·统考高考真题）函数的最小正周期和最大值分别是（ ）
A．和B．和2C．和D．和2
3．（2020·北京·统考高考真题）若函数的最大值为2，则常数的一个取值为 ．
1．（2023·全国·统考高考真题）已知实数满足，则的最大值是（ ）
A．B．4C．D．7
2．（2023·湖北襄阳·襄阳四中校考模拟预测）若函数的最小值为，则常数的一个取值为 .（写出一个即可）
3．（2023·云南曲靖·曲靖一中校考模拟预测）已知则函数的最大值为 .
4．（2023·浙江宁波·统考一模）若，则 ．
考点五、三角恒等变换的综合应用
1．（2023·吉林延边·统考二模）下列化简不正确的是（ ）
A．B．
C．D．
2．（2023·江苏·校联考模拟预测）若，则（ ）
A．0B．C．1D．
3．（2023·陕西咸阳·武功县普集高级中学校考模拟预测）已知为第二象限角，，则（ ）
A．B．
C．D．
4．（2023·山西朔州·怀仁市第一中学校校考模拟预测）已知为锐角，且，则 .
1．（2023·山西吕梁·统考三模）已知，则的近似值为（ ）
A．B．C．D．
2．（2023·江苏无锡·校联考三模）已知，，若，则（ ）
A．B．C．D．
3．（2023·安徽亳州·安徽省亳州市第一中学校考模拟预测）已知，若，则（ ）
A．B．C．D．
4．（2023·河北·校联考一模）函数的最小值为 .
【基础过关】
一、单选题
1．（2023·四川成都·四川省成都市玉林中学校考模拟预测）设，则等于（ ）
A．-2B．2C．-4D．4
2．（2023·山东威海·统考二模）已知，则（ ）
A．B．C．D．
3．（2023·湖南长沙·雅礼中学校考模拟预测）已知，，则（ ）
A．4B．6C．D．
4．（2023·辽宁锦州·统考模拟预测）已知直线的倾斜角为，则（ ）
A．-3B．C．D．
5．（2023·吉林通化·梅河口市第五中学校考模拟预测）若，，则（ ）
A．1B．C．D．
6．（2023·河南·襄城高中校联考三模）已知，，则（ ）
A．B．C．D．
7．（2023·黑龙江哈尔滨·哈师大附中校考模拟预测）已知锐角，满足，则的值为（ ）
A．1B．C．D．
8．（2023·河南·襄城高中校联考模拟预测）已知，，，则（ ）
A．B．C．D．1
二、填空题
9．（2023·河北·统考模拟预测）已知，则 .
10．（2023·辽宁·朝阳市第一高级中学校联考三模）若，则的值为 ．
【能力提升】
一、单选题
1．（2023·江苏镇江·江苏省镇江第一中学校考模拟预测）已知角，满足，，则（ ）
A．B．C．D．2
2．（2023·四川宜宾·宜宾市叙州区第一中学校校考模拟预测）已知，则（ ）
A．B．C．D．
3．（2023·四川·模拟预测）设，，，则有（ ）
A．B．C．D．
4．（2023·贵州遵义·统考三模）已知锐角满足，则（ ）
A．B．C．D．1
5．（2023·湖北·荆门市龙泉中学校联考模拟预测）若，，则等于（ ）
A．B．C．D．
6．（2023·山东·潍坊一中校联考模拟预测）设，则（ ）
A．B．
C．D．
7．（2023·江苏无锡·校联考三模）设，，，则（ ）
A．B．C．D．
二、多选题
8．（2023·海南海口·统考模拟预测）已知锐角，，满足，则（ ）
A．，可能是方程的两根
B．若，则
C．
D．
三、填空题
9．（2023·上海闵行·上海市七宝中学校考二模）若函数的最小值为，则常数的一个取值为 .
10．（2023·云南保山·统考二模）已知角的顶点为坐标原点，始边与x轴的非负半轴重合，点在角的终边上，则 .
【真题感知】
一、单选题
1．（全国·高考真题）的值是（ ）
A．B．C．D．
2．（全国·高考真题）的值等于（ ）
A．B．C．D．
3．（全国·高考真题）若，则的值为（ ）
A．B．C．D．
4．（安徽·高考真题）函数的最小正周期为（ ）
A．B．C．D．
5．（全国·高考真题）函数的最小正周期是( )
A．B．C．D．
6．（湖北·高考真题）已知，，则（ ）
A．B．C．D．
7．（2023·全国·统考高考真题）过点与圆相切的两条直线的夹角为，则（ ）
A．1B．C．D．
二、多选题
8．（2021·全国·统考高考真题）已知为坐标原点，点，，，，则（ ）
A．B．
C．D．
三、填空题
9．（上海·高考真题）函数的最小正周期为
10．（2004·全国·高考真题）函数的最大值为 ．4年考情
考题示例
考点分析
关联考点
2023年新I卷，第8题,5分
用和、差角的正弦公式化简、求值
二倍角的余弦公式
三角函数求值
2023年新Ⅱ卷，第7题,5分
半角公式、二倍角的余弦公式
无
2023年新Ⅱ卷，第16题,5分
由图象确定正(余)弦型函数解析式
特殊角的三角函数值
2022年新Ⅱ卷，第6题,5分
用和、差角的余弦公式化简、求值
用和、差角的正弦公式化简、求值
无
2021年新I卷，第6题,5分
二倍角的正弦公式
正、余弦齐次式的计算
三角函数求值
2021年新I卷，第10题,5分
逆用和、差角的余弦公式化简、求值二倍角的余弦公式
数量积的坐标表示
坐标计算向量的模