2024沧州七县联考高一上学期10月期中考试数学含答案

这是一份2024沧州七县联考高一上学期10月期中考试数学含答案，共60页。试卷主要包含了选择题，多选题，填空题，解答题等内容，欢迎下载使用。
一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.
1. 已知集合，则（ ）
A. B.
C. D.
2. 命题“”的否定形式是
A. B.
C. D.
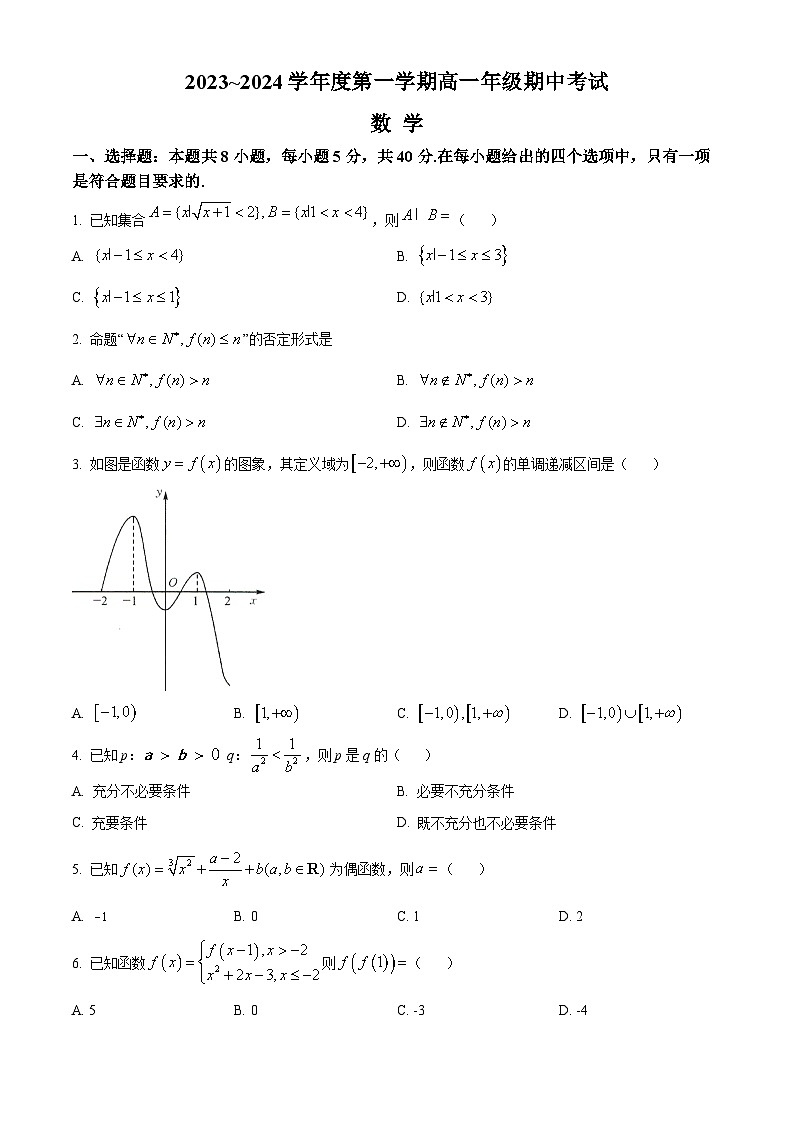
3. 如图是函数的图象，其定义域为，则函数的单调递减区间是（ ）
A. B. C. D.
4. 已知p： q：，则p是q的（ ）
A. 充分不必要条件B. 必要不充分条件
C. 充要条件D. 既不充分也不必要条件
5. 已知偶函数，则（ ）
A. B. 0C. 1D. 2
6. 已知函数则（ ）
A. 5B. 0C. -3D. -4
7. 不等式的解集为（ ）
A. B.
C. 或D. 或
8. 已知幂函数的图象经过点，则函数在区间上的最大值是（ ）
A. 2B. 1C. D. 0
二、多选题：本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，部分选对的得2分，有选错的得0分.
9. 下列函数中，表示同一个函数的是（ ）
A. 与
B 与
C 与
D. 与
10. 若集合A，B，U满足，则（ ）
A. B. C. D.
11. 已知正数满足，则下列说法一定正确的是（ ）
A. B. C. D.
12. 已知函数的定义域为A，若对任意，存在正数M，使得成立，则称函数是定义在A上的“有界函数”.则下列函数是“有界函数”的是（ ）
A. B.
C. D.
三、填空题：本题共4小题，每小题5分，共20分.
13. 函数的定义域是__________.
14. 满足的集合的个数为__________.
15 若，则f(x)＝________.
16. 已知函数是定义在上的奇函数，且，若对任意的，当时，都有成立，则不等式的解集为__________.
四、解答题：本题共6小题，共70分.解答应写出文字说明､证明过程或演算步骤.
17. 已知为实数，，．
（1）当时，求的取值集合；
（2）当时，求的取值集合.
18. 已知函数．
（1）求证：在上单调递减；在上单调递增；
（2）当时，求函数的值域．
19. 已知.
（1）当时，若同时成立，求实数的取值范围；
（2）若是的充分不必要条件，求实数的取值范围.
20. 如果向一杯糖水里加糖，糖水变甜了，这其中蕴含着著名的糖水不等式：．
（1）证明榶水不等式；
（2）已知是三角形的三边，求证：．
21. 某企业投资144万元用于火力发电项目，年内的总维修保养费用为（）万元，该项目每年可给公司带来100万元的收入．假设到第n年年底，该项目的纯利润为y万元．（纯利润＝累计收入－总维修保养费用－投资成本）
（1）写出纯利润y的表达式，并求该项目从第几年起开始盈利；
（2）随着中国光伏产业的高速发展，集群效应及技术的不断革新带来了成本的进一步降低．经过慎重考虑，该公司决定投资太阳能发电项目，针对现有火力发电项目，有以下两种处理方案：
①年平均利润最大时，以12万元转让该项目；
②纯利润最大时，以4万元转让该项目．
你认为以上哪种方案最有利于该公司的发展？请说明理由．
22. 已知是定义在上的单调递增函数，且.
（1）解不等式；
（2）若对和恒成立，求实数取值范围.2023~2024学年度第一学期高一年级期中考试
数学
一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.
1. 已知集合，则（ ）
A. B.
C D.
【答案】D
【解析】
【分析】先求出集合，再根据交集运算求.
【详解】集合，所以，
故选：D.
2. 命题“”的否定形式是
A. B.
C. D.
【答案】C
【解析】
【详解】试题分析：命题的否定是把结论否定，同时存在量词与全称量词要互换，命题“”的否定形式“”．故选C．
考点：命题的否定．
3. 如图是函数的图象，其定义域为，则函数的单调递减区间是（ ）
A. B. C. D.
【答案】C
【解析】
【分析】根据图像判断单调性，解题时需注意单调区间不能用.
【详解】若函数单调递减，则对应图象呈下降趋势，由图知，的单调递减区间为和，
故选：C.
4. 已知p： q：，则p是q的（ ）
A. 充分不必要条件B. 必要不充分条件
C. 充要条件D. 既不充分也不必要条件
【答案】A
【解析】
【分析】根据与的互相推出情况判断出属于何种条件.
【详解】当时，，所以，所以充分性满足，
当时，取，此时不满足，所以必要性不满足，
所以是的充分不必要条件，
故选：A.
5. 已知为偶函数，则（ ）
A. B. 0C. 1D. 2
【答案】D
【解析】
【分析】根据偶函数的性质，结合求解并检验即可.
【详解】解：因为为偶函数，
所以，，解得，
所以，检验，为偶函数，符合题意．
故选：D．
6. 已知函数则（ ）
A. 5B. 0C. -3D. -4
【答案】B
【解析】
【分析】代入求解即可.
【详解】.
故选：B.
7. 不等式的解集为（ ）
A. B.
C. 或D. 或
【答案】B
【解析】
【分析】由一元二次不等式的解法求解．
【详解】不等式可化为，即，解得．
故选：B
8. 已知幂函数的图象经过点，则函数在区间上的最大值是（ ）
A. 2B. 1C. D. 0
【答案】C
【解析】
【分析】根据幂函数经过的点可得，进而利用换元法，结合二次函数的性质即可求解.
【详解】设
，令，
由于在区间上单调递增，在上单调递减，
在区间上的最大值是.
故选：C.
二、多选题：本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，部分选对的得2分，有选错的得0分.
9. 下列函数中，表示同一个函数的是（ ）
A. 与
B. 与
C. 与
D. 与
【答案】CD
【解析】
【分析】根据函数的定义域以及对应关系是否相同，即可结合选项逐一求解.
【详解】对于A,的定义域为的定义域为，两函数的定义域不相同，
所以不是同一个函数，故A错误；
对于B，的定义域为的定义域为，两函数的定义域相同，
因为，所以两函数的对应关系不相同，所以两函数不是同一个函数，故B错误；
对于C，的定义域为，两函数的定义域相同，对应关系也相同，
所以是同一个函数，故C正确；
对于D，的定义域为的定义域为，两函数的定义域相同，而且两函数的对应关系相同，
所以两函数是同一个函数，故D正确.
故选:CD.
10. 若集合A，B，U满足，则（ ）
A. B. C. D.
【答案】AD
【解析】
【分析】根据韦恩图即可得之间的关系，进而结合选项即可逐一求解.
【详解】
由知：与没有共同的元素，故，故A正确，
∴，即B错误；仅当时，即C错误；，即D正确．
故选：AD．
11. 已知正数满足，则下列说法一定正确的是（ ）
A. B. C. D.
【答案】AD
【解析】
【分析】由基本不等式对选项逐一判断．
【详解】由，得．
对于A，（当且仅当，即时取等号），A正确；
对于B，（当且仅当，即），B错误；
对于C，（当且仅当，即时取等号），
，解得（当且仅当时取等号），C错误；
对于D，（当且仅当，即时取等号），由C知（当且仅当时取等号），
（当且仅当时取等号），D正确．
故选：AD
12. 已知函数的定义域为A，若对任意，存在正数M，使得成立，则称函数是定义在A上的“有界函数”.则下列函数是“有界函数”的是（ ）
A. B.
C. D.
【答案】BCD
【解析】
【分析】“有界函数”值域需要有界，化简各函数，并求出函数的值域，然后进行判断.
【详解】对于A，，由于，所以，所以，故不存在正数M，使得成立.
对于B，令，则，，所以，故存在正数1，使得成立.
对于C，令，则，易得.所以，即，故存在正数5，使得成立.
对于D，令，则，，则，易得，所以，故存在正数，使得成立.
故选：BCD.
三、填空题：本题共4小题，每小题5分，共20分.
13. 函数的定义域是__________.
【答案】
【解析】
【分析】根据解析式建立不等式求解即可.
【详解】由，即，解得，
即函数的定义域是.
故答案为：
14. 满足的集合的个数为__________.
【答案】3
【解析】
【分析】根据子集的定义以及包含关系即可列举求解.
【详解】因为，所以可以为，共计3个.
故答案为：3
15. 若，则f(x)＝________.
【答案】且
【解析】
【分析】换元法求函数的解析式，同时注意定义域问题.
【详解】令，则，
因为，所以，
又且，所以且，
所以且，
故答案为：且
16. 已知函数是定义在上的奇函数，且，若对任意的，当时，都有成立，则不等式的解集为__________.
【答案】
【解析】
【分析】根据函数为奇函数，则为偶函数，又已知得函数在上单调递减，可得函数在在上单调递增，又，可得不等式与的解集，进而得到解集.
【详解】令，则为偶函数，且，
当时，为减函数，
所以当或时，；
当或时，；
因此当时，；当时，，
即不等式的解集为.
故答案为：
四、解答题：本题共6小题，共70分.解答应写出文字说明､证明过程或演算步骤.
17. 已知为实数，，．
（1）当时，求的取值集合；
（2）当时，求的取值集合.
【答案】（1）
（2）
【解析】
【分析】（1）分、两种情况讨论，求出集合，根据可得出关于的等式，即可求得实数的值；
（2）分、、且三种情况，求出集合、，根据可得出关于的等式，即可解得实数的值.
【小问1详解】
解：因为，
所以当时，，当时，．
又，所以，此时，满足．
所以当时，的取值集合为．
小问2详解】
解：当时，，不成立；
当时，，，成立；
当且时，，，由，得，所以．
综上，的取值集合为．
18 已知函数．
（1）求证：在上单调递减；在上单调递增；
（2）当时，求函数的值域．
【答案】（1）证明见解析；
（2）.
【解析】
【分析】（1）由单调性定义求解，
（2）由换元法求解，
【小问1详解】
证明：，，且，
有．
由，，且，得，，
所以，即．
所以在上单调递减．
同理，当，，且，有．
故在上单调递增．
【小问2详解】
由（1）得在上单调递减；在上单调递增．
，，所以．
令，则，，
由（1）得在上单调递增，所以．
故函数的值域为．
19. 已知.
（1）当时，若同时成立，求实数的取值范围；
（2）若是的充分不必要条件，求实数的取值范围.
【答案】（1）
（2）
【解析】
【分析】（1）化简，当时，解出，求它们的交集即可；
（2）是的充分不必要条件，即所对应的集合所对应的集合，结合包含关系，即可求.
【小问1详解】
当时，，即，
，即，
若同时成立，则，
即实数的取值范围为.
【小问2详解】
由（1）知，，
，
即，
①当时，，
若是的充分不必要条件，则，解得；
②当时，，此时不可能是的充分不必要条件，不符合题意.
综上，实数的取值范围为.
20. 如果向一杯糖水里加糖，糖水变甜了，这其中蕴含着著名的糖水不等式：．
（1）证明榶水不等式；
（2）已知是三角形的三边，求证：．
【答案】（1）证明见解析
（2）证明见解析
【解析】
【分析】（1）由作差法证明；
（2）由糖水不等式变形证明．
【小问1详解】
，
因为，所以，
所以，即．
小问2详解】
因为是三角形的三边，所以，
由（1）知，
同理，
所以，
所以原不等式成立．
21. 某企业投资144万元用于火力发电项目，年内的总维修保养费用为（）万元，该项目每年可给公司带来100万元的收入．假设到第n年年底，该项目的纯利润为y万元．（纯利润＝累计收入－总维修保养费用－投资成本）
（1）写出纯利润y的表达式，并求该项目从第几年起开始盈利；
（2）随着中国光伏产业的高速发展，集群效应及技术的不断革新带来了成本的进一步降低．经过慎重考虑，该公司决定投资太阳能发电项目，针对现有火力发电项目，有以下两种处理方案：
①年平均利润最大时，以12万元转让该项目；
②纯利润最大时，以4万元转让该项目．
你认为以上哪种方案最有利于该公司的发展？请说明理由．
【答案】（1），第4年起开始盈利
（2）选择方案①更有利于该公司的发展，理由见解析
【解析】
【分析】（1）根据题意得到，解不等式得到答案.
（2）分别利用均值不等式和二次函数性质计算利润的最大值，再对比时间得到答案.
【小问1详解】
由题意可知，
令，得，解得，
所以从第4年起开始盈利．
【小问2详解】
若选择方案①，设年平均利润为万元，
则，
当且仅当，即时等号成立，所以当时，取得最大值12，
此时该项目共获利（万元）．
若选择方案②，纯利润，
因为，所以当或8时，取得最大值80，此时该项目共获利（万元）．
以上两种方案获利均为84万元，但方案①只需6年，而方案②至少需7年，所以仅考虑该项目的获利情况时，选择方案①更有利于该公司的发展．
22. 已知是定义在上的单调递增函数，且.
（1）解不等式；
（2）若对和恒成立，求实数的取值范围.
【答案】（1）解集为
（2）
【解析】
【分析】（1）由，不等式，化为，结合单调性，即可求；
（2） 恒成立问题较为最值问题，即在恒成立，进而转化为求在恒成立，对和讨论即可.
【小问1详解】
是定义在上的单调递增函数，且，
则，即.
有,解得，
故所求解集为.
【小问2详解】
在上单调递增，
当时，.
问题转化为，
即，对成立.
接下来求的取值范围.
设，
①若，则，对成立；
②若，则是关于的一次函数，要使，对成立，必须，且，
或.
或或，即的取值范围是.