北师大版数学八年级下册考点梳理+精讲精练专题05 全等三角形七大模型（2份打包，原卷版+含解析）

这是一份北师大版数学八年级下册考点梳理+精讲精练专题05 全等三角形七大模型（2份打包，原卷版+含解析），文件包含部编七年级上册语文第五单元教材知识点考点梳理pptx、部编七年级上册语文第五单元教材知识点考点梳理教案docx、部编七年级上册语文第五单元教材知识点考点梳理验收卷原卷版docx、部编七年级上册语文第五单元教材知识点考点梳理验收卷解析版docx等4份课件配套教学资源，其中PPT共31页， 欢迎下载使用。
K型(一线三垂直)模型 二、“手拉手”模型
三、倍长中线 四、平行线中点
五、“雨伞”模型 六、半角模型
七、胖瘦模型
一、K型(一线三垂直)模型

两条手臂之间的距离=长手十短手， 两条手臂之间的距离-长手一短手，
即DE=AD+CE， 即DE=AD-E，
一线三重直果中考考试中常见的模型，模型按照常规的方法需要找到对应三角形边角关系，进而得全等三角形，根据全等三角形再找所求的边角.但很多常见的一线三重直模型可以先尝试找到“长手"和“短手”，根据模型快速解题.
二、“手拉手”模型

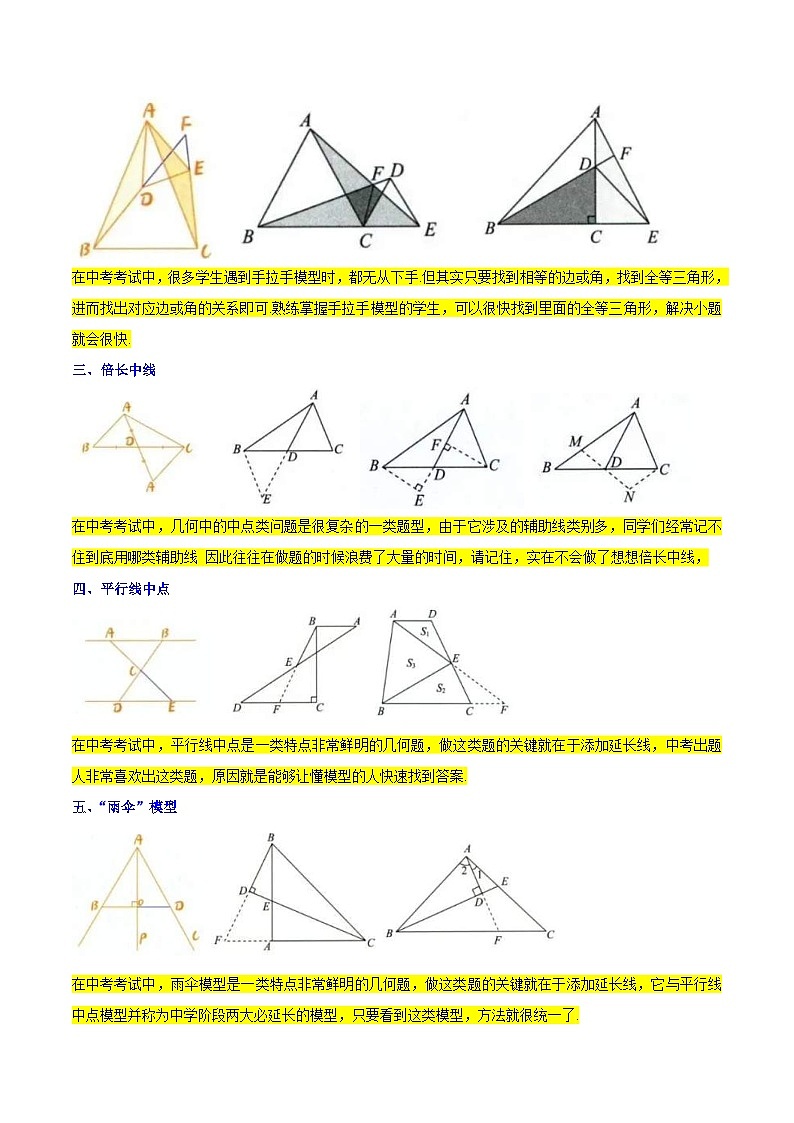
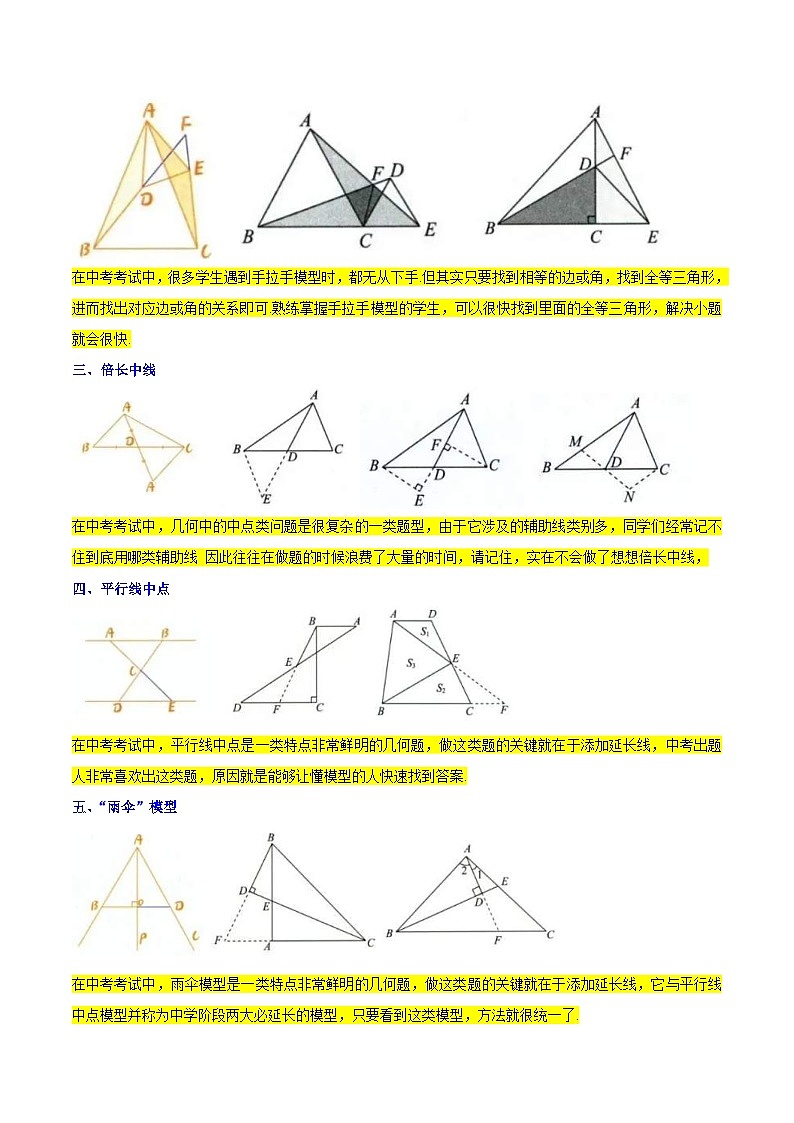
在中考考试中，很多学生遇到手拉手模型时，都无从下手.但其实只要找到相等的边或角，找到全等三角形，进而找出对应边或角的关系即可.熟练掌握手拉手模型的学生，可以很快找到里面的全等三角形，解决小题就会很快.
三、倍长中线

在中考考试中，几何中的中点类问题是很复杂的一类题型，由于它涉及的辅助线类别多，同学们经常记不住到底用哪类辅助线 因此往往在做题的时候浪费了大量的时间，请记住，实在不会做了想想倍长中线，
四、平行线中点

在中考考试中，平行线中点是一类特点非常鲜明的几何题，做这类题的关键就在于添加延长线，中考出题人非常喜欢出这类题，原因就是能够让懂模型的人快速找到答案.
五、“雨伞”模型

在中考考试中，雨伞模型是一类特点非常鲜明的几何题，做这类题的关键就在于添加延长线，它与平行线中点模型并称为中学阶段两大必延长的模型，只要看到这类模型，方法就很统一了.
六、半角模型

在中考考试中，半角模型在选择题、填空题、解答题中经常出现，我们在处理这类问题时，关键在于找到半角和全角，运用口诀进行旋转，进行边角转化，就能很快地解决此类问题.
七、胖瘦模型

全等三角形果中考必考内容，是解决有关线段、角等问题的一个出发点.胖瘦模型的特点很鲜明，但是很多学生没有进行总结，所以看到这种题果没有方向的，如果惜这类问题的解决方法，你会发现要做出答案其实果很轻松的。
K型(一线三垂直)模型
一．填空题（共2小题）
1．（2022春•武昌区期中）如图，四边形ABCD中，∠B＝∠C＝90°，点E是BC边上一点，△ADE是等边三角形，若，＝ ．
2．（2022春•朝阳区校级期中）勾股定理有着悠久的历史，它曾引起很多人的兴趣．1955年希腊发行了以勾股定理为背景的邮票．如图，在Rt△ABC中，∠BAC＝90°，AC＝3，AB＝4．分别以AB，AC，BC为边向外作正方形ABMN，正方形ACKL，正方形BCDE，并按如图所示作长方形HFPQ，延长BC交PQ于G．则长方形CDPG的面积为 ．
二．解答题（共6小题）
3．（2021秋•余干县校级期中）如图，在△ABC中，AB＝AC，BC，AB边上的高AD，CE相交于点F，且AE＝CE．
（1）求证：△AEF≌△CEB；
（2）若AF＝12，求CD的长．
4．（2021春•嘉祥县期中）如图1，以△ABC的边AB为边，向外画正方形ABDE，过点A作AM⊥BC于M，过点E作EP⊥MA交MA延长线于点P．
（1）则EP＝ ；（直接填写图中与EP相等的一条线段）
（2）如图2，若∠BAC＝90°，以AC为边再向外画正方形ACFG，连接EG交PM于点N，求证：EN＝GN；
（3）若∠BAC是钝角或锐角，请仿照图2分别在图3、图4中补画图形，并选“＞”或“＜”或“＝”其中一个符号填空，直接表示此时EN与GN的大小关系．
如图3，若∠BAC＞90°，则EN GN；
如图4，若∠BAC＜90°，则EN GN．
5．（2021春•禹州市期中）如图，在四边形ABCD中，∠ABC＝90°，AB＝8，BC＝15，CD＝17，AD＝17，连接AC，BD．
（1）证明∠ACD是直角；
（2）求对角线BD的长．
6．（2021春•丹阳市期中）通过对下面数学模型的研究学习，解决下列问题：
【模型呈现】
（1）如图1，∠BAD＝90°，AB＝AD，过点B作BC⊥AC于点C，过点D作DE⊥AC于点E．由∠1+∠2＝∠2+∠D＝90°，得∠1＝∠D．又∠ACB＝∠AED＝90°，可以推理得到△ABC≌△DAE．进而得到AC＝ ，BC＝AE．我们把这个数学模型称为“K字”模型或“一线三等角”模型；
【模型应用】
（2）如图2，∠BAD＝∠CAE＝90°，AB＝AD，AC＝AE，连接BC，DE，且BC⊥AF于点F，DE与直线AF交于点G．求证：点G是DE的中点；
【深入探究】
（3）如图3，已知四边形ABCD和DEGF为正方形，△AFD的面积为S1，△DCE的面积为S2，则有S1 S2（填“＞、＝、＜”）；
（4）如图4，分别以△DCE的三条边为边，向外作正方形，连接AF、GK、BH．当AB＝4，DE＝，∠CDE＝45°时，图中的三个阴影三角形的面积和为 ；
（5）如图5，点A、B、C、D、E都在同一条直线上，四边形ABKH、KCMG、DENM都是正方形，若该图形总面积是16，正方形KCMG的面积是4，则△HKG的面积是 ．
7．（2022春•淮阴区校级期中）（1）【问题初探】
苏科版教材八年级下册第九章《中心对称图形一一平行四边形》复习题中有这样的问题：如图1正方形ABCD的边长为2，∠EOF的顶点O在正方形ABCD两条对角线的交点处，∠EOF＝90°，将∠EOF绕点O旋转，∠EOF的两边分别与正方形ABCD的边BC和CD交于点E和点F（点F与点C，D不重合），问：在旋转过程中，四边形OECF的面积会发生变化吗？证明你的结论．
爱思考的浩浩和小航同学分别探究出了如下两种解题思路：
浩浩：如图a，充分利用正方形对角线垂直、相等且互相平分等性质证明了△OEC≌△OFD，则S△OEC＝S△OFD，那么S四边形OECF＝S△OEC+S△OCF＝S△OFD+S△OCF＝S△OCD，这样，就实现了四边形OECF的面积向△OCD面积的转化；
小航：如图b，也是考虑到正方形对角线的特征，过点O分别作OG⊥BC于点G，OH⊥CD于点H，证明△OGE≌△OHF，从而将四边形OECF的面积转化成了小正方形OGCH的面积．
通过他们的思路点拨，你认为：S四边形OECF＝ （填一个数值），其实，在这样的旋转变化过程中，线段CE与CF的和也是一个定值，为 ．
（2）【类比探究】
①如图2，矩形ABCD中，AB＝2，AD＝4，点O是AD边的中点，∠EOF＝90°，点E在AB上，点F在BC上，则四边形EBFO的面积为 ；EB+BF＝ ；
②如图3，若将（1）中的“正方形ABCD”改为“∠BCD＝120°，边长为8的菱形ABCD，其他条件不变，当∠EOF＝60°时，四边形OECF的面积还是一个定值吗？是，请求出来；不是，请说明理由；
③如图4，在②的条件下，当点O在对角线AC上运动，顶点O与B点的距离为7，且∠EOF旋转至CF＝1时，CE的长度为 ．
（3）【拓展延伸】
如图5，∠BOD＝α（α为钝角），∠CAD＝180°﹣α，∠BAC是钝角，OA平分∠BOD，OD＝，OB＝4，AB＝，OA＝1，点C是OB上一点，那么OC的长为 ．
8．（2022秋•永年区期中）在△ABC中，∠ACB＝90°，AC＝BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E，
（1）当直线MN绕点C旋转到图（1）的位置时，显然有：DE＝AD+BE；
（2）当直线MN绕点C旋转到图（2）的位置时，求证：DE＝AD﹣BE；
（3）当直线MN绕点C旋转到图（3）的位置时，试问DE、AD、BE具有怎样的等量关系？请直接写出这个等量关系．
二、“手拉手”模型
一．解答题（共9小题）
1．（2022春•开福区校级期中）如图，在△ABC和△AEF中，点E在BC边上，∠C＝∠F，AC＝AF，∠CAF＝∠BAE，EF与AC交于点G．
（1）求证：AE＝AB；
（2）若∠B＝62°，∠C＝24°，求∠EAC的度数．
2．（2021春•铜梁区校级期中）已知，如图，在▱ABCD中，点F是▱ABCD内一点，AB⊥BF，AB＝BF，过点F作FE⊥AD，垂足为点E．
（1）如图1，若BF＝3EF＝6，求四边形ABFE的面积；
（2）如图2，连接BE、CE，若BE＝CE，求证：AE+EF＝BC．
3．（2022春•章丘区期中）感知：如图①，△ABC和△AED都是等腰直角三角形，∠BAC＝∠DAE＝90°，点B在线段AD上，点C在线段AE上，我们很容易得到BD＝CE，不需证明．
探究：如图②，将△AED绕点A逆时针旋转α（0＜α＜90°），连结BD和CE，此时BD＝CE是否依然成立？若成立，写出证明过程；若不成立，说明理由．
应用：如图③，当△ADE绕点A逆时针旋转，使得点D落在BC的延长线上，连结CE．
①∠ACE的度数为 度；
②线段BC、CD、CE之间的数量关系是 ；
③若AB＝AC＝，CD＝1，则线段DE的长为 ．
4．（2022春•清城区期中）如图，在平面直角坐标系中，点A的坐标为（1，0），以线段OA为边在第四象限内作等边三角形AOB，点C为x轴正半轴上动点（OC＞1），连接BC，以线段BC为边在第四象限内作等边△CBD，连接DA并延长交y轴于点E．
（1）求证：△OBC≌△ABD．
（2）在点C的运动过程中，∠CAD的度数是否会变化？如果不变，请求出∠CAD的度数；如果变化，请说明理由．
（3）以A，E，C为顶点的三角形是等腰三角形时，直接写出此时点C的坐标和CD的长度．
5．（2022春•和平区校级期中）已知：点D是△ABC边BC所在直线上的一个动点（点D与点B，C不重合），∠BAC＝90°，AB＝AC＝2，连接DA，点D绕点A顺时针转90°得到点E，连接BE，AE，DE．
（1）如图1，当点D在线段CB的延长线上时，请你判断线段BE与线段CD之间的关系，并证明你判断的结论．
（2）如图2，当点D在线段BC上，且BD＝2CD时，直接写出四边形AEBC的面积．
（3）点D绕点A逆时针转90°得到点F，连接CF，AF，DF，当∠EAB＝15°时，直接写出线段CF的长．
6．（2022春•介休市期中）已知△ABC和△ADE都是等腰三角形，且AB＝AC，AD＝AE，∠DAE＝∠BAC．
（1）[初步感知]如图①，当点D、E分别落在边AB、AC上时，那么DB EC．（填＜、＞或＝）
（2）[发现证明]如图②，将图①中的△ADE绕点A旋转，当点D在△ABC外部，点E在△ABC内部时，求证：DB＝EC；
（3）[深入研究]如图③，如果△ABC和△ADE都是等边三角形，且点C、E、D在同一条直线上，则∠CDB的度数为 ；线段CE、BD之间的数量关系为 ；
（4）[拓展应用]如图④，如果△ABC和△ADE都是等腰直角三角形，∠BAC＝∠DAE＝90°，点C、D、E在同一直线上，作AM⊥DE，若AB＝，BD＝，求AM的长．
7．（2022春•吉安期中）如图，在平面直角坐标系中，点A的坐标（2，0），点C是y轴上的动点，当点C在y轴上移动时，始终保持△ACP是等边三角形（点A、C、P按逆时针方向排列）；当点C移动到O点时，得到等边三角形AOB（此时点P与点B重合）．
（1）点B的坐标为 ，直线AB的表达式为 ．
（2）点C在y轴上移动过程中，当等边三角形ACP的顶点P在第二象限时，连接BP，求证：△AOC≌△ABP；
（3）当点C在y轴上移动时，点P也随之运动，探究点P在移动过程中有怎样的规律？请将这个规律用函数关系式表达出来；
（4）点C在y轴上移动过程中，当△OBP为等腰三角形时，直接写出点P的坐标．
8．（2021春•将乐县期中）（1）如图1，△ABC与△ADE均是顶角为40°的等腰三角形，BC、DE分别是底边，求证：BD＝CE；
（2）如图2，△ACB和△DCE均为等边三角形，点A、D、E在同一直线上，连接BE．
填空：∠AEB的度数为 ；线段BE与AD之间的数量关系是 ．
（3）拓展探究
如图3，△ACB和△DCE均为等腰直角三角形，∠ACB＝∠DCE＝90°，点A、D、E在同一直线上，CM为△DCE中DE边上的高，连接BE．请判断∠AEB的度数及线段CM、AE、BE之间的数量关系，并说明理由．
9．（2022春•椒江区校级期中）我们规定：有一组邻边相等，且这组邻边的夹角为60°的凸四边形叫做“准筝形”．
（1）如图1，在四边形ABCD中，∠A+∠C＝270°，∠D＝30°，AB＝CB，求证：四边形ABCD是“准筝形”；
（2）小军同学研究“准筝形”时，思索这样一道题：如图2，“准筝形”ABCD，AD＝BD，∠BAD＝∠BCD＝60°，BC＝5，CD＝3，求AC的长．
小军研究后发现，可以CD为边向外作等边三角形，构造手拉手全等模型，用转化的思想来求AC．请你按照小军的思路求AC的长．
（3）如图3，在△ABC中，∠A＝45°，∠ABC＝120°，BC＝2，设D是△ABC所在平面内一点，当四边形ABCD是“准筝形”时，请直接写出四边形ABCD的面积．
三、倍长中线
一．填空题（共1小题）
1．（2022春•游仙区校级期中）如图，在△ABC中，BC＝10，点D是BC边上一动点，BE⊥AD交AD于点E，当BE＝4时，△ABD的面积恰好等于△ADC的面积，连接CE，则此时CE＝ ．
二．解答题（共4小题）
2．（2021春•玉林期中）如图，在▱ABCD中，点E是CD的中点，点F是BC边上的一点，且EF⊥AE．
求证：AE平分∠DAF．
李华同学读题后有一个想法，延长FE，AD交于点M，要证AE平分∠DAF，只需证△AMF是等腰三角形即可．请你参考李华的想法，完成此题的证明．
3．（2021秋•甘南县校级期中）如图，AD是△ABC的中线，E、F分别在AB、AC上，且DE⊥DF 求证：BE+CF＞EF．
4．（2019春•玄武区期中）课外兴趣小组活动时，老师提出了如下问题：
（1）如图1，在△ABC中，若AB＝5，AC＝3，求BC边上的中线AD的取值范围．
小明在组内经过合作交流，得到了如下的解决方法：延长AD到E，使得DE＝AD，再连接BE（或将△ACD绕点D逆时针旋转180°得到△EBD），把AB、AC、2AD集中在△ABE中，利用三角形的三边关系可得2＜AE＜8，则1＜AD＜4．
[感悟]解题时，条件中若出现“中点”“中线”字样，可以考虑构造以中点为对称中心的中心对称图形，把分散的已知条件和所求证的结论集中到同一个三角形中．
（2）解决问题：受到（1）的启发，请你证明下列命题：如图2，在△ABC中，D是BC边上的中点，DE⊥DF，DE交AB于点E，DF交AC于点F，连接EF．
求证：BE+CF＞EF，若∠A＝90°，探索线段BE、CF、EF之间的等量关系，并加以证明．
5．（2019春•秦淮区期中）阅读理解：课外兴趣小组活动时，老师提出了如下问题：
如图1，△ABC中，若AB＝5，AC＝3，求BC边上的中线AD的取值范围．
小明在组内经过合作交流，得到了如下的解决方法：延长AD到E，使得DE＝AD，再连接BE（或将△ACD绕点D逆时针旋转180°得到△EBD），把AB、AC、2AD集中在△ABE中，利用三角形的三边关系可得2＜AE＜8，则1＜AD＜4．
感悟：解题时，条件中若出现“中点”“中线”字样，可以考虑构造以中点为对称中心的中心对称图形，把分散的已知条件和所求证的结论集中到同一个三角形中．
（1）问题解决：受到（1）的启发，请你证明下面命题：如图2，在△ABC中，D是BC边上的中点，DE⊥DF，DE交AB于点E，DF交AC于点F，连接EF．
①求证：BE+CF＞EF；②若∠A＝90°，探索线段BE、CF、EF之间的等量关系，并加以证明；
（2）问题拓展：如图3，在平行四边形ABCD中，AD＝2AB，F是AD的中点，作CE⊥AB，垂足E在线段AB上，联结EF、CF，那么下列结论①∠DCF＝∠BCD；②EF＝CF；③S△BEC＝2S△CEF；④∠DFE＝3∠AEF．其中一定成立是 （填序号）．
四、平行线中点
一．选择题（共2小题）
1．（2021春•鄞州区校级期中）矩形ABCD与ECFG如图放置，点B，C，F共线，点C，E，D共线，连接AG，取AG的中点H，连接EH．若AB＝CF＝4，BC＝CE＝2，则EH＝（ ）
A．B．2C．D．
2．（2022春•鄞州区期中）如图，在平行四边形ABCD中，AD＝2，AB＝，∠B是锐角，AE⊥BC于点E，F是AB的中点，连接DF、EF．若∠EFD＝90°，则AE长为（ ）
A．2B．C．D．
二．填空题（共1小题）
3．（2022春•清江浦区校级期中）如图，在△ACD中，∠CAD＝90°，AC＝6，AD＝10，AB∥CD，E是CD上一点，BE交AD于点F，若AB＝DE，则图中阴影部分的面积为 ．
三．解答题（共2小题）
4．（2021春•扶沟县期中）如图，已知AB＝12，AB⊥BC于B，AB⊥AD于A，AD＝5，BC＝10．点E是CD的中点，求AE的长．
5．（2022春•澄迈县期中）（1）方法回顾证明：三角形中位线定理．
已知：如图1，DE是△ABC的中位线．求证： ．
证明：
（2）问题解决：如图2，在正方形ABCD中，E为AD的中点，G、F分别为AB、CD边上的点，若AG＝3，DF＝4，∠GEF＝90°，求GF的长．
五、“雨伞”模型
一．选择题（共1小题）
1．（2022秋•新洲区期中）如图，BP是∠ABC的平分线，AP⊥BP于P，连接PC，若△ABC的面积为1cm2，则△PBC的面积为（ ）
A．0.4cm2B．0.5cm2C．0.6cm2D．不能确定
二．填空题（共1小题）
2．（2022春•芙蓉区校级期中）如图，在Rt△ABC中，∠B＝90°，AD平分∠BAC交BC于点D，DE垂直平分AC，垂足为点E，若BD＝1，则BC的长为 ．
三．解答题（共3小题）
3．（2021春•高州市期中）如图，在△ABC中，已知D是BC的中点，过点D作BC的垂线交∠BAC的平分线于点E，EF⊥AB于点F，EG⊥AC于点G．
（1）求证：BF＝CG；
（2）若AB＝12，AC＝8，求线段CG的长．
4．（2021春•驿城区校级期中）如图，在△ABC中，AD平分∠BAC，∠C＝90°，DE⊥AB于点E，点F在AC上，BD＝DF．
（1）求证：CF＝EB．
（2）若AB＝20，AC＝16，求AF的长．
5．（2021春•黄骅市期中）如图，在△ABC中，点D为边BC的中点，点E在△ABC内，AE平分∠BAC，CE⊥AE，点F在AB上，且BF＝DE．
（1）求证：四边形BDEF是平行四边形；
（2）线段AB，BF，AC之间具有怎样的数量关系？证明你所得到的结论．
六、半角模型
一．选择题（共1小题）
1．（2021春•牡丹区期中）如图，在Rt△ABC中，AB＝AC，D、E是斜边BC上两点，且∠DAE＝45°，将△ADC绕点A顺时针旋转90°后，得到△AFB，连接EF，下列结论：
①△AED≌△AEF；②∠FAD＝90°；③BE+DC＝DE④BE2+DC2＝DE2，其中一定正确的是（ ）
A．①③B．①②④C．①②③④D．②④
二．解答题（共7小题）
2．（2021秋•同江市期中）已知：正方形ABCD中，∠MAN＝45°，∠MAN绕点A顺时针旋转，它的两边分别交CB、DC（或它们的延长线）于点M、N．当∠MAN绕点A旋转到BM＝DN时（如图1），易证BM+DN＝MN．
（1）当∠MAN绕点A旋转到BM≠DN时（如图2），线段BM、DN和MN之间有怎样的数量关系？写出猜想，并加以证明；
（2）当∠MAN绕点A旋转到如图3的位置时，线段BM、DN和MN之间又有怎样的数量关系？请直接写出你的猜想．
3．（2021春•丽水期中）已知正方形ABCD中，M，N是边BC，CD上任意两点，∠MAN＝45°，连结MN．
（1）如图①，请直接写出BM，DN，MN三条线段的数量关系： ；
（2）如图②，过点A作AH⊥MN于点H，求证：AB＝AH；
（3）如图③，已知∠MAN＝45°，AH⊥MN于点H，且MH＝2，NH＝3，求AH的长．
4．（2021春•福田区校级期中）探究：
（1）如图1，在正方形ABCD中，E、F分别是BC、CD上的点，且∠EAF＝45°，试判断BE、DF与EF三条线段之间的数量关系，直接写出判断结果： ；
（2）如图2，若把（1）问中的条件变为“在四边形ABCD中，AB＝AD，∠B+∠D＝180°，E、F分别是边BC、CD上的点，且∠EAF＝∠BAD”，则（1）问中的结论是否仍然成立？若成立，请给出证明，若不成立，请说明理由；
（3）在（2）问中，若将△AEF绕点A逆时针旋转，当点分别E、F运动到BC、CD延长线上时，如图3所示，其它条件不变，则（1）问中的结论是否发生变化？若变化，请给出结论并予以证明．
5．（2022秋•市南区期中）已知正方形ABCD中，∠MAN＝45°，∠MAN绕点A顺时针旋转，它的两边分别交CB，DC（或它们的延长线）于点M，N，AH⊥MN于点H．
（1）如图①，当∠MAN绕点A旋转到BM＝DN时，请你直接写出AH与AB的数量关系： ；
（2）如图②，当∠MAN绕点A旋转到BM≠DN时，（1）中发现的AH与AB的数量关系还成立吗？如果不成立请写出理由，如果成立请证明；
（3）如图③，已知∠MAN＝45°，AH⊥MN于点H，且MH＝2，AH＝6，求NH的长．（可利用（2）得到的结论）
6．（2022春•鄞州区校级期中）已知，正方形ABCD中，∠MAN＝45°，∠MAN绕点A顺时针旋转，它的两边分别交CB、DC（或它们的延长线）于点M、N，AH⊥MN于点H．
（1）如图①，当∠MAN绕点A旋转到BM＝DN时，请你直接写出AH与AB的数量关系： ；
（2）如图②，当∠MAN绕点A旋转到BM≠DN时，（1）中发现的AH与AB的数量关系还成立吗？如果不成立请写出理由，如果成立请证明；
（3）如图③，已知∠MAN＝45°，AH⊥MN于点H，且MH＝2，NH＝3，求AH的长．（可利用（2）得到的结论）
7．（2021秋•千山区期中）（1）如图1，正方形ABCD中，点E，F分别在边BC，CD上，∠EAF＝45°，延长CD到点G，使DG＝BE，连接EF，AG．求证：EF＝FG．
（2）如图2，等腰直角三角形ABC中，∠BAC＝90°，AB＝AC，点M，N在边BC上，且∠MAN＝45°，若BM＝1，CN＝3，求MN的长．
8．（2015春•平度市期中）已知：△ABC是等边三角形，△BDC是等腰三角形，其中∠BDC＝120°，过点D作∠EDF＝60°，分别交AB于E，交AC于F，连接EF．
（1）若BE＝CF，求证：①△DEF是等边三角形；②BE+CF＝EF．
（2）若BE≠CF，即E、F分别是线段AB，AC上任意一点，BE+CF＝EF还会成立吗？请说明理由．
七、胖瘦模型
一．选择题（共1小题）
1．（2022春•清江浦区校级期中）如图，D是AB上一点，DF交AC于点E，DE＝FE，FC∥AB，若AB＝6，CF＝4，则BD的长是（ ）
A．1.5B．2C．2.5D．3
二．填空题（共2小题）
2．（2021春•灌阳县期中）如图，在Rt△ABC和Rt△DEF中，∠B＝∠E＝90°，AC＝DF，AB＝DE，若∠A＝55°，则∠DFE＝ ．
3．（2022春•镇海区校级期中）如图，已知△ABC是边长为6的等边三角形，点D是边BC上的一点，且BD＝2，以AD为边作等边△ADE，过点E作EF∥BC，交AC于点F，连接BF，则S四边形BDEF＝ ．
三．解答题（共2小题）
4．（2021春•扶沟县期中）如图，在△ABC中，∠ACB＝90°，AC＝BC，点P在斜边AB上，以PC为直角边作等腰直角三角形PCQ，∠PCQ＝90°，则PA2，PB2，PC2三者之间的数量关系是 ，请说明理由．（提示：连接BQ）
5．（2022春•崇义县期中）定义：一组邻边相等且对角互补的四边形叫做“等补四边形”．
如图1，四边形ABCD中，AD＝CD，∠A+∠C＝180°，则四边形ABCD叫做“等补四边形”．
（1）概念理解
①在以下四种图形中，一定是“等补四边形”的是 ．
A．平行四边形
B．菱形
C．矩形
D．正方形
②等补四边形ABCD中，若∠B：∠C：∠D＝2：3：4，则∠A＝ ．
（2）知识运用
如图1，在四边形ABCD中，BD平分∠ABC，AD＝CD，BC＞BA．求证：四边形ABCD是等补四边形．
（3）探究发现
如图2，在等补四边形ABCD中，AB＝AD，连接AC，AC是否平分∠BCD？请说明理由．