第02讲 圆的方程及直线与圆、圆与圆的位置关系（5类核心考点精讲精练）-备战2024年高考数学一轮复习（新教材新高考）

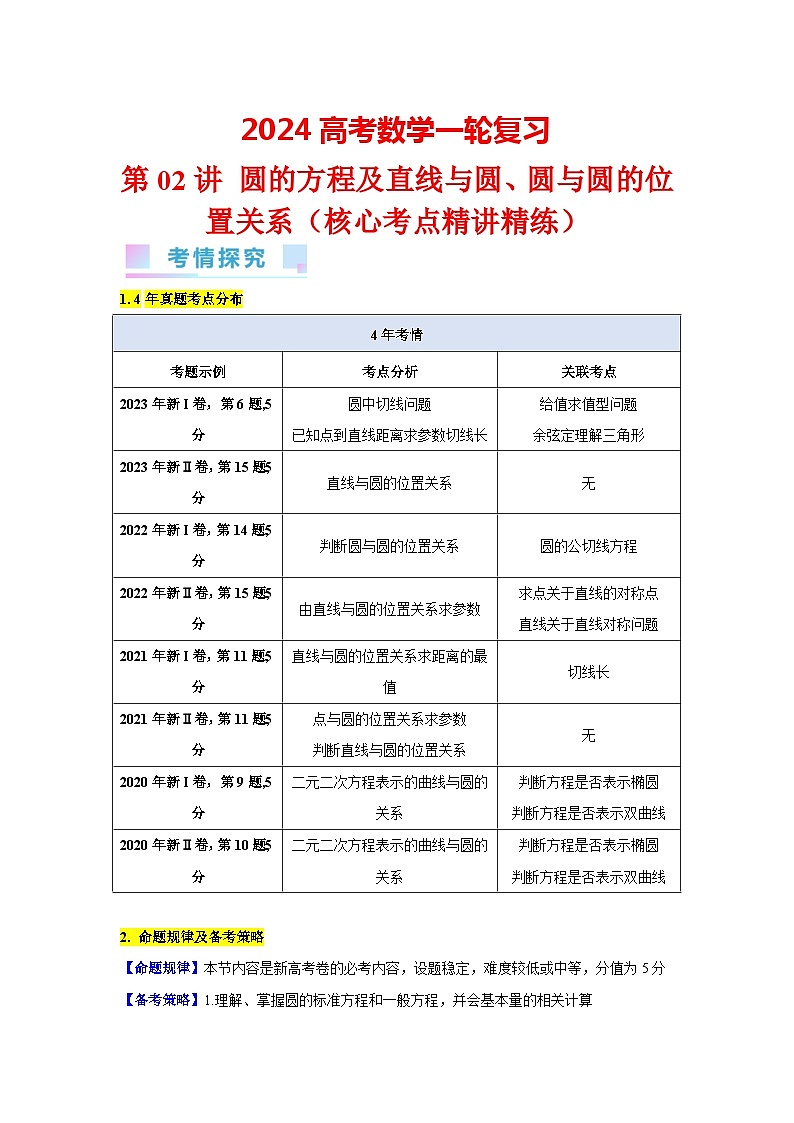
这是一份第02讲 圆的方程及直线与圆、圆与圆的位置关系（5类核心考点精讲精练）-备战2024年高考数学一轮复习（新教材新高考），共4页。试卷主要包含了 4年真题考点分布， 命题规律及备考策略，能利用圆中关系进行相关参数求解，会解决圆中的最值问题等内容，欢迎下载使用。
2024高考数学一轮复习
第02讲 圆的方程及直线与圆、圆与圆的位置关系（核心考点精讲精练）

1. 4年真题考点分布
4年考情
考题示例
考点分析
关联考点
2023年新I卷，第6题,5分
圆中切线问题
已知点到直线距离求参数切线长
给值求值型问题
余弦定理解三角形
2023年新Ⅱ卷，第15题,5分
直线与圆的位置关系
无
2022年新I卷，第14题,5分
判断圆与圆的位置关系
圆的公切线方程
2022年新Ⅱ卷，第15题,5分
由直线与圆的位置关系求参数
求点关于直线的对称点
直线关于直线对称问题
2021年新I卷，第11题,5分
直线与圆的位置关系求距离的最值
切线长
2021年新Ⅱ卷，第11题,5分
点与圆的位置关系求参数
判断直线与圆的位置关系
无
2020年新I卷，第9题,5分
二元二次方程表示的曲线与圆的关系
判断方程是否表示椭圆
判断方程是否表示双曲线
2020年新Ⅱ卷，第10题,5分
二元二次方程表示的曲线与圆的关系
判断方程是否表示椭圆
判断方程是否表示双曲线

2. 命题规律及备考策略
【命题规律】本节内容是新高考卷的必考内容，设题稳定，难度较低或中等，分值为5分
【备考策略】1.理解、掌握圆的标准方程和一般方程，并会基本量的相关计算
2.能正确处理点与圆、直线与圆及圆与圆的位置关系求解
3.能利用圆中关系进行相关参数求解
4.会解决圆中的最值问题
【命题预测】本节内容是新高考卷的必考内容，一般考查直线与圆和圆与圆的几何综合，需强化练习



知识讲解
1. 圆的标准方程
，其中圆心坐标为，半径为
2. 圆的一般方程
（）
配方可得：，
圆心坐标为，半径为
3. 表示圆的充要条件

4. 点与圆的位置关系
已知点，圆的方程为：
若，点在圆内
若，点在圆上
若，点在圆外
5. 直线与圆的位置关系
直线，圆
代数关系，其中为联立方程根的个数，
几何关系，其中为圆心到直线的距离

6. 圆与圆的位置关系
设圆的半径为，设圆的半径为，两圆的圆心距为
若，两圆外离，若，两圆外切，若，两圆内切
若，两圆相交，若，两圆内含，若，同心圆
两圆外离，公切线的条数为4条；两圆外切，公切线的条数为3条；
两圆相交，公切线的条数为2条；两圆内切，公切线的条数为1条；
两圆内含，公切线的条数为0条；

7. 弦长公式
设，，
则
或：
8. 圆上一点到圆外一点的距离的最值

9. 圆上一点到圆上一点的距离的最值

10. 圆上一点到直线距离的最值

11. 过圆内一点的最长弦和最短弦
最长弦：直径；最短弦：垂直于直径

考点一、圆的标准方程

1．（2023·全国·高三专题练习）已知的顶点，，，则其外接圆的方程为（    ）
A． B．
C． D．
【答案】A
【分析】先设圆的方程为，根据题意，列出方程组求解，即可求出结果.
【详解】设的外接圆的方程为，
因为的顶点，，，
所以，解得，
因此即为所求圆的方程.
故选：A.
【点睛】本题主要考查求圆的标准方程，利用待定系数法求解即可，属于基础题型.
2．（2023·全国·高三专题练习）已知圆心为的圆与直线相切，则该圆的标准方程是（    ）
A． B．
C． D．
【答案】A
【分析】由圆心到切线的距离等于半径，求出圆的半径，即可得到本题答案.
【详解】因为圆心为的圆与直线相切，所以圆心到直线的距离等于半径，即，
所以该圆的标准方程是．
故选：A
3．（2023·全国·高三专题练习）求过两点，且圆心在直线上的圆的标准方程是（    ）
A． B．
C． D．
【答案】D
【分析】由圆心在直线x﹣2y﹣2＝0上，可设圆心C（2b+2，b），再根据圆心到两点A（0，4）、B（4，6）的距离相等，求出b的值，即得圆心和半径，从而求得圆的标准方程．
【详解】设圆心坐标为C（2b+2，b），由圆过两点A（0，4），B（4，6），可得|AC|=|BC|，
即，解得，
可得圆心为（4，1），半径为5，则所求圆的方程为．
故选：D．
4．（2023·全国·高三专题练习）已知圆的圆心为，其一条直径的两个端点恰好在两坐标轴上，则这个圆的方程是（    ）
A． B．
C． D．
【答案】A
【分析】根据中点坐标公式求出直径两端点的坐标，然后求出半径，再求出圆的方程即可.
【详解】设直径的两个端点分别，
圆心C为点由中点坐标公式，得，解得
∴半径，
∴圆的方程是即
故选：A.
5．（2023·全国·高三专题练习）经过直线与圆的两个交点，且面积最小的圆的方程是（    ）
A． B．
C． D．
【答案】C
【分析】当所求圆的直径就是圆与直线相交的弦时，所求圆的面积最小．然后将结合图形求解圆心和半径即可求解；
【详解】  
由题可知，当所求圆的直径就是圆与直线相交的弦时，所求圆的面积最小．
圆，即圆，
所以圆心坐标为，半径为3，
弦心距，弦长为，则所求圆的半径为2,
接下来求解所求圆的圆心位置P：
所以，
过圆的圆心和直线垂直的直线方程为：，即．
最小圆的圆心为与直线的交点，
解方程组可得，
所求面积最小的圆方程为．
故选：C．


1．（2023·全国·高三专题练习）若的三个顶点坐标分别为，，，则外接圆的圆心坐标为（    ）
A． B． C． D．
【答案】C
【分析】求出线段的中点的坐标即得解.
【详解】解：由题得是直角三角形，且.
所以的外接圆的圆心就是线段的中点，
由中点坐标公式得.
故选：C
2．（2023·全国·高三专题练习）过，，三点的圆的一般方程是（    ）
A． B．
C． D．
【答案】D
【分析】设所求的圆的方程为，代入已知点得方程组，求解可得圆的方程.
【详解】解：设所求的圆的方程为，因为，，三点在圆上，所以解得于是所求圆的一般方程是.
故选：D.
3．（2023·全国·高三专题练习）若圆经过点，，且圆心在直线：上，则圆的方程为（    ）
A． B．
C． D．
【答案】A
【分析】求解的中垂线方程，然后求解圆的圆心坐标，求解圆的半径，然后得到圆的方程.
【详解】圆经过点，，
可得线段的中点为，又，
所以线段的中垂线的方程为，
即，
由，解得，
即，圆的半径，
所以圆的方程为.
故选：A.
4．（2023·贵州铜仁·统考模拟预测）过、两点，且与直线相切的圆的方程可以是（    ）
A． B．
C． D．
【答案】C
【分析】分析可知，圆心在直线上，设圆心为，根据圆与直线相切以及圆过点可得出关于的等式，解出的值，即可得出所求圆的方程.
【详解】因为、，则线段的垂直平分线所在直线的方程为，
设圆心为，则圆的半径为，
又因为，所以，，
整理可得，解得或，
当时，，此时圆的方程为；
当时，，此时圆的方程为.
综上所述，满足条件的圆的方程为或.
故选：C.
5．（2023·宁夏·六盘山高级中学校考一模）圆心在直线上，且过点的圆的标准方程为 ．
【答案】
【分析】先求得点与点确定线段的中垂线，再根据直线上，两方程联立求得圆心，从而得到圆的半径即可.
【详解】解：点与点确定直线的斜率为，其中点为，
所以线段的中垂线方程为，即，
又圆心在直线上，
由，解得，
所以圆心为，，
所以圆的标准方程为，
故答案为：


考点二、圆的一般方程

1．（2023·全国·高三专题练习）若圆：过坐标原点，则实数的值为（    ）
A．2或1 B．-2或-1 C．2 D．-1
【答案】C
【分析】根据圆的一般方程的定义，结合过原点列方程即可求解.
【详解】∵表示圆，
∴
∴.
又圆过原点，
∴，
∴或（舍去）；
.
故选:C.
2．（2023·全国·高三专题练习）已知方程表示圆，则实数m的取值范围为（    ）
A． B． C． D．
【答案】D
【分析】根据题意得到，再解不等式即可.
【详解】因为方程表示圆，
所以，解得.
故选：D
3．（2023·甘肃定西·统考模拟预测）若点在圆的外部，则a的取值范围是（    ）
A． B． C． D．
【答案】C
【分析】利用表示圆的条件和点和圆的位置关系进行计算.
【详解】依题意，方程可以表示圆，则，得；
由点在圆的外部可知：，得.
故.
故选：C


1．（2023·贵州·校联考模拟预测）已知曲线的方程，则“”是“曲线是圆”的（    ）
A．必要不充分条件 B．充分不必要条件
C．充要条件 D．既不充分也不必要条件
【答案】A
【分析】根据二元二次方程表示圆的条件、必要不充分条件的定义可得答案.
【详解】，即，
∴曲线是圆，∴“”是“”的必要不充分条件.
故选：A.
2．（2023·全国·高三专题练习）若点在圆C：的外部，则实数k的取值范围是（    ）
A． B．
C． D．
【答案】C
【分析】由题意可得，解不等式组即可得实数k的取值范围.
【详解】因为点在圆C：的外部，
所以，解得.
故实数k的取值范围是.
故选:C.
3．（2023·江西吉安·宁冈中学校考一模）已知点是圆上的动点，则的最大值为（    ）
A． B． C．6 D．5
【答案】A
【分析】根据圆的标准方程，设x、y的参数方程，利用辅助角公式及正弦型函数的性质求最值即可.
【详解】由，令，则，
所以当时，的最大值为.
故选：A


考点三、直线与圆的位置关系

1．（2021·北京·统考高考真题）已知直线（为常数）与圆交于点，当变化时，若的最小值为2，则    
A． B． C． D．
【答案】C
【分析】先求得圆心到直线距离，即可表示出弦长，根据弦长最小值得出
【详解】由题可得圆心为，半径为2，
则圆心到直线的距离，
则弦长为，
则当时，取得最小值为，解得.
故选：C.
2．（2020·全国·统考高考真题）若过点（2，1）的圆与两坐标轴都相切，则圆心到直线的距离为（    ）
A． B． C． D．
【答案】B
【分析】由题意可知圆心在第一象限，设圆心的坐标为，可得圆的半径为，写出圆的标准方程，利用点在圆上，求得实数的值，利用点到直线的距离公式可求出圆心到直线的距离.
【详解】由于圆上的点在第一象限，若圆心不在第一象限，
则圆与至少与一条坐标轴相交，不合乎题意，所以圆心必在第一象限，
设圆心的坐标为，则圆的半径为，
圆的标准方程为.
由题意可得，
可得，解得或，
所以圆心的坐标为或，
圆心到直线的距离均为；
圆心到直线的距离均为
圆心到直线的距离均为；
所以，圆心到直线的距离为.
故选：B.
【点睛】本题考查圆心到直线距离的计算，求出圆的方程是解题的关键，考查计算能力，属于中等题.
3．（2023·全国·统考高考真题）过点与圆相切的两条直线的夹角为，则（    ）
A．1 B． C． D．
【答案】B
【分析】方法一：根据切线的性质求切线长，结合倍角公式运算求解；方法二：根据切线的性质求切线长，结合余弦定理运算求解；方法三：根据切线结合点到直线的距离公式可得，利用韦达定理结合夹角公式运算求解.
【详解】方法一：因为，即，可得圆心，半径，
过点作圆C的切线，切点为，
因为，则，
可得，
则，
，
即为钝角，
所以；
法二：圆的圆心，半径，
过点作圆C的切线，切点为，连接，
可得，则，
因为
且，则，
即，解得，
即为钝角，则，
且为锐角，所以；
方法三：圆的圆心，半径，
若切线斜率不存在，则切线方程为，则圆心到切点的距离，不合题意；
若切线斜率存在，设切线方程为，即，
则，整理得，且
设两切线斜率分别为，则，
可得，
所以，即，可得，
则，
且，则，解得.
故选：B.
    
4．（2021·全国·统考高考真题）（多选）已知直线与圆，点，则下列说法正确的是（    ）
A．若点A在圆C上，则直线l与圆C相切 B．若点A在圆C内，则直线l与圆C相离
C．若点A在圆C外，则直线l与圆C相离 D．若点A在直线l上，则直线l与圆C相切
【答案】ABD
【分析】转化点与圆、点与直线的位置关系为的大小关系，结合点到直线的距离及直线与圆的位置关系即可得解.
【详解】圆心到直线l的距离，
若点在圆C上，则，所以，
则直线l与圆C相切，故A正确；
若点在圆C内，则，所以，
则直线l与圆C相离，故B正确；
若点在圆C外，则，所以，
则直线l与圆C相交，故C错误；
若点在直线l上，则即，
所以，直线l与圆C相切，故D正确.
故选：ABD.
5．（2021·全国·统考高考真题）（多选）已知点在圆上，点、，则（    ）
A．点到直线的距离小于
B．点到直线的距离大于
C．当最小时，
D．当最大时，
【答案】ACD
【分析】计算出圆心到直线的距离，可得出点到直线的距离的取值范围，可判断AB选项的正误；分析可知，当最大或最小时，与圆相切，利用勾股定理可判断CD选项的正误.
【详解】圆的圆心为，半径为，
直线的方程为，即，
圆心到直线的距离为，
所以，点到直线的距离的最小值为，最大值为，A选项正确，B选项错误；
如下图所示：

当最大或最小时，与圆相切，连接、，可知，
，，由勾股定理可得，CD选项正确.
故选：ACD.
【点睛】结论点睛：若直线与半径为的圆相离，圆心到直线的距离为，则圆上一点到直线的距离的取值范围是.
6．（2022·全国·统考高考真题）设点，若直线关于对称的直线与圆有公共点，则a的取值范围是 ．
【答案】
【分析】首先求出点关于对称点的坐标，即可得到直线的方程，根据圆心到直线的距离小于等于半径得到不等式，解得即可；
【详解】解：关于对称的点的坐标为，在直线上，
所以所在直线即为直线，所以直线为，即；
圆，圆心，半径，
依题意圆心到直线的距离，
即，解得，即；
故答案为：
7．（2020·浙江·统考高考真题）设直线与圆和圆均相切，则 ；b= ．
【答案】
【分析】由直线与两圆相切建立关于k，b的方程组，解方程组即可.
【详解】设，，由题意，到直线的距离等于半径，即，，
所以，所以（舍）或者，
解得.
故答案为：
【点晴】本题主要考查直线与圆的位置关系，考查学生的数学运算能力，是一道基础题.


1．（2023·湖南永州·统考一模）在平面直角坐标系中，过直线上一点作圆的两条切线，切点分别为，则的最大值为（    ）
A． B． C． D．
【答案】A
【分析】由题意圆的标准方程为，如图，又，所以，又由圆心到直线的距离可求出的最小值，进而求解.
【详解】如下图所示：
  
由题意圆的标准方程为，，
又因为，所以，
所以，
又圆心到直线的距离为，
所以，所以不妨设，
则，
又因为在单调递增，所以当且仅当即，即当且仅当直线垂直已知直线时，
有最大值.
故选：A.
2．（2020·全国·统考高考真题）已知⊙M：，直线：，为上的动点，过点作⊙M的切线，切点为，当最小时，直线的方程为（    ）
A． B． C． D．
【答案】D
【分析】由题意可判断直线与圆相离，根据圆的知识可知，四点共圆，且，根据 可知，当直线时，最小，求出以 为直径的圆的方程，根据圆系的知识即可求出直线的方程．
【详解】圆的方程可化为，点 到直线的距离为，所以直线 与圆相离．
依圆的知识可知，四点四点共圆，且，所以，而 ，
当直线时，， ，此时最小．
∴即 ，由解得， ．
所以以为直径的圆的方程为，即 ，
两圆的方程相减可得：，即为直线的方程．
故选：D.
【点睛】本题主要考查直线与圆，圆与圆的位置关系的应用，以及圆的几何性质的应用，意在考查学生的转化能力和数学运算能力，属于中档题．
3．（2023·全国·统考高考真题）已知实数满足，则的最大值是（    ）
A． B．4 C． D．7
【答案】C
【分析】法一：令，利用判别式法即可；法二：通过整理得，利用三角换元法即可，法三：整理出圆的方程，设，利用圆心到直线的距离小于等于半径即可.
【详解】法一：令，则，
代入原式化简得，
因为存在实数，则，即，
化简得，解得，
故 的最大值是，
法二：，整理得，
令，，其中，
则，
，所以，则，即时，取得最大值，
法三：由可得，
设，则圆心到直线的距离，
解得
故选：C.
4．（2023·河北保定·统考二模）（多选）已知直线，圆的圆心坐标为，则下列说法正确的是（    ）
A．直线恒过点
B．
C．直线被圆截得的最短弦长为
D．当时，圆上存在无数对点关于直线对称
【答案】ABD
【分析】求解直线系结果的定点判断A；圆的圆心求解、判断B；求解直线被圆截的弦长判断C，利用圆的圆心到直线的距离判断D．
【详解】直线，恒过点，所以A正确；
圆的圆心坐标为，，，所以B正确；
圆的圆心坐标为，圆的半径为2．
直线，恒过点，圆的圆心到定点的距离为：，
直线被圆截得的最短弦长为，所以C不正确；

当时，直线方程为：，经过圆的圆心，所以圆上存在无数对点关于直线对称，所以D正确．
故选：ABD．
5．（2020·天津·统考高考真题）已知直线和圆相交于两点．若，则的值为 ．
【答案】5
【分析】根据圆的方程得到圆心坐标和半径，由点到直线的距离公式可求出圆心到直线的距离，进而利用弦长公式，即可求得．
【详解】因为圆心到直线的距离，
由可得，解得．
故答案为：．
【点睛】本题主要考查圆的弦长问题，涉及圆的标准方程和点到直线的距离公式，属于基础题．
6．（2021·天津·统考高考真题）若斜率为的直线与轴交于点，与圆相切于点，则 ．
【答案】
【分析】设直线的方程为，则点，利用直线与圆相切求出的值，求出，利用勾股定理可求得.
【详解】设直线的方程为，则点，
由于直线与圆相切，且圆心为，半径为，
则，解得或，所以，
因为，故.
故答案为：.

7．（2022·天津·统考高考真题）若直线与圆相交所得的弦长为，则 ．
【答案】
【分析】计算出圆心到直线的距离，利用勾股定理可得出关于的等式，即可解得的值.
【详解】圆的圆心坐标为，半径为，
圆心到直线的距离为，
由勾股定理可得，因为，解得.
故答案为：.


考点四、圆与圆的位置关系

1．（2023·全国·高三专题练习）已知圆与圆，则圆与圆的位置关系为（    ）
A．相交 B．外切 C．外离 D．内含
【答案】B
【分析】确定两圆的圆心和半径，由圆心间的距离与半径的关系即可得解.
【详解】圆化成标准方程为，圆心，半径为，
圆，圆心，半径为，
，圆与圆的位置关系为外切，
故选：B
2．（2023·山西·校联考模拟预测）已知圆和交于A，B两点，则（    ）
A． B． C． D．
【答案】B
【分析】先求得相交弦所在直线方程，然后根据圆的弦长的求法求得.
【详解】将和相减得直线，
点到直线的距离，
所以．
故选：B
3．（2023·全国·高三专题练习）圆：与圆：公切线的条数为（    ）
A．1 B．2 C．3 D．4
【答案】C
【分析】首先根据题意得到两圆相外切，即可得到答案.
【详解】根据题意，圆：，即，
其圆心为，半径；
圆：，即，
其圆心为，半径，
两圆的圆心距，所以两圆相外切，
其公切线条数有3条．
故选：C．
4．（2023·全国·高三专题练习）若圆与圆有且仅有3条公切线，则m=（    ）
A．14 B．28 C．9 D．
【答案】A
【分析】分别求出两圆的圆心及半径，再根据圆与圆有且仅有3条公切线，可得两圆外切，则，从而可得答案.
【详解】圆的圆心，半径，
圆的圆心，半径，
因为圆与圆有且仅有3条公切线，
所以两圆外切，
则，
即，解得.
故选：A.
5．（2023·福建龙岩·统考二模）已知M是圆上一个动点，且直线：与直线：（，）相交于点P，则的最小值是（    ）
A． B． C． D．
【答案】D
【分析】根据直线过定点及垂直关系确定P轨迹，结合圆的位置关系求最值即可.
【详解】  
由两直线方程可知分别过定点，且两直线互相垂直，
设的中点为，则，
如图所示，则两直线的交点的轨迹为以为圆心为直径的圆，，
可知两圆相离，设直线交圆于E，交圆于D，
显然.
故选：D
6．（2023·广西北海·统考一模）已知圆：与：恰好有4条公切线，则实数的取值范围是（    ）
A． B．
C． D．
【答案】D
【分析】根据两圆有4条公切线，得到两圆外离，然后根据外离列不等式，解不等式即可得的取值范围.
【详解】因为圆：与：恰好有4条公切线，所以圆与外离，所以，解得或，即实数的取值范围是.
故选：D.


1．（2023·全国·高三专题练习）已知圆：，圆：，则与的位置关系是（    ）
A．外切 B．内切 C．相交 D．外离
【答案】C
【分析】算出两圆圆心的距离，然后与两圆半径之和、差比较即可.
【详解】圆的圆心为，
圆的圆心为，
所以
所以圆与的位置关系是相交.
故选: C.
2．（2022·全国·统考高考真题）写出与圆和都相切的一条直线的方程 ．
【答案】或或
【分析】先判断两圆位置关系，分情况讨论即可.
【详解】[方法一]：
显然直线的斜率不为0，不妨设直线方程为，
于是，
故①，于是或，
再结合①解得或或，
所以直线方程有三条，分别为，，
填一条即可
[方法二]：
设圆的圆心，半径为，
圆的圆心，半径，
则，因此两圆外切，

由图像可知，共有三条直线符合条件，显然符合题意；
又由方程和相减可得方程，
即为过两圆公共切点的切线方程，
又易知两圆圆心所在直线OC的方程为，
直线OC与直线的交点为，
设过该点的直线为，则，解得，
从而该切线的方程为填一条即可
[方法三]：
圆的圆心为，半径为，
圆的圆心为，半径为，
两圆圆心距为，等于两圆半径之和，故两圆外切，
如图，

当切线为l时，因为，所以，设方程为
O到l的距离，解得，所以l的方程为，
当切线为m时，设直线方程为，其中，，
由题意，解得，
当切线为n时，易知切线方程为，
故答案为：或或.

3．（2023·山西·校联考模拟预测）已知圆：的圆心到直线的距离为，则圆与圆：的公切线共有（    ）
A．0条 B．1条 C．2条 D．3条
【答案】B
【分析】先根据题意求得，从而得到两圆的圆心和半径，进而求得圆心距等于两半径的差，得知两圆内切，即可知道公切线只有1条.
【详解】圆：的圆心为，半径为a，
所以圆心到直线的距离为，解得或．
因为，所以.
所以圆：的圆心为，半径为．
圆：的标准方程为，
圆心坐标为，半径，
圆心距，所以两圆相内切．
所以两圆的公切线只有1条.
故选：B．
4．（2023·全国·模拟预测）已知圆与圆交于，两点，点在圆上，则点到直线距离的最大值为（    ）
A．6 B． C． D．7
【答案】B
【分析】由两个圆的方程相减消去平方项可得直线的方程，根据直线的方程可得直线经过定点，再求出圆心的坐标和圆的半径，求出圆心到直线的距离的最大值可得点到直线距离的最大值.
【详解】因为，所以，
由和可得直线的方程为，
变形得，由，得，
所以直线经过定点，
因为圆的圆心为，半径，
所以点到直线的距离的最大值为，
所以点到直线距离的最大值为.
故选：B
5．（2023春·吉林白山·高三统考期中）已知圆与圆外切，直线与圆C相交于A，B两点，则（    ）
A．4 B．2 C． D．
【答案】D
【分析】由两圆外切列方程求，再求圆心到直线的距离，结合弦长公式求弦长.
【详解】圆的圆心的坐标为，半径为，
圆的圆心的坐标为，半径为，
因为圆O与圆C外切，所以
所以.
设圆心到直线l的距离为d，则，
从而.
故选：D.
6．（2023·安徽滁州·安徽省定远中学校考模拟预测）已知圆与圆相交所得的公共弦长为，则圆的半径（    ）
A． B． C．或1 D．
【答案】D
【分析】两圆方程相减可得公共弦所在直线方程，后由垂径定理结合圆圆心与半径表达式可得答案.
【详解】与两式相减得，即公共弦所在直线方程.
圆方程可化为，可得圆心，半径.则圆心到的距离为，
半弦长为，则有，解得或（舍），此时
故选：.

考点五、圆中的最值问题综合

1．（2023·湖北武汉·华中师大一附中校考模拟预测）已知直线上的两点，且，点为圆上任一点，则的面积的最大值为（    ）
A． B． C． D．
【答案】A
【分析】找到圆上的点到直线距离的最大值作为的高，再由面积公式求解即可.
【详解】把圆变形为，
则圆心，半径，
圆心到直线的距离，
则圆上的点到直线的距离的最大值为，又，
∴的面积的最大值为．
故选：A．
2．（2023·福建宁德·校考一模）已知圆与直线，P，Q分别是圆C和直线l上的点且直线PQ与圆C恰有1个公共点，则的最小值是（    ）
A． B． C． D．
【答案】A
【分析】，的最小值为圆心到直线的距离，可求的最小值.
【详解】圆化为标准方程为，
则圆C的圆心为，半径，则，
直线PQ与圆C相切，有，
因为点Q在直线l上，所以，则．
即的最小值是.
故选：A
3．（2023·河北邯郸·统考三模）在平面直角坐标系内，已知，，动点满足，则（）的最小值是（    ）
A． B．2 C．4 D．16
【答案】C
【分析】由题意求出点P的轨迹方程，则可以看成圆上动点与定直线上动点的距离，求得其最小值，即可求得答案.
【详解】因为，，动点满足，
则，整理得，
可以看成圆上动点与定直线上动点的距离，
其最小值为圆心到直线的距离减去圆的半径2，即，
因此，的最小值是，
故选：C.
4．（2023·山东·模拟预测）已知动点的轨迹方程为，定点，则的最小值为（    ）
A． B． C． D．
【答案】C
【分析】取，连接，，确定，变换得到，计算得到答案.
【详解】如图所示：取，连接，，则，
  
故，故，
，
当三点共线且在线段上时等号成立，
故选：C
5．（2023·四川·校联考模拟预测）已知点，，，若点是的外接圆上一点，则点到直线：的距离的最大值为（    ）
A． B． C． D．14
【答案】C
【分析】设所求圆的方程为，根据的三个顶点分别为，，，代入求得方程，再判断直线与圆的位置关系，然后转化为点与圆的位置关系求解.
【详解】解：设所求圆的方程为，
因为的三个顶点分别为，，，
则，
解得，
所以外接圆的一般方程为，
其圆心为，半径为5，
因为直线，即，
所以点到直线的距离为，
所以直线与的外接圆相离，
所以点到直线的距离的最大值为.
故选：.
6．（2023·安徽·合肥一中校联考模拟预测）（多选）已知正三角形ABC的边长为2，点D为边BC的中点.若内一动点M满足.则下列说法中正确的有（    ）
A．线段BM长度的最大为 B．的最大值为
C．面积的最小值为 D．的最小值为
【答案】BD
【分析】以点为原点建立平面直角坐标系，求出动点的轨迹方程，再根据圆上得点到定点和定直线的距离的最值问题即可判断AC；由即可判断B；取最小值时，取最大值，也即与圆相切时，即可判断D.
【详解】如图，以点为原点建立平面直角坐标系，
则，设，
由，得，
化简得，
故动点的轨迹是一个以圆心为，半径的圆不含原点，
A项：，所以，故A错误；
B项：
，故B正确；
C项：直线，即，
圆心到直线的距离为，
则点到直线的距离的最小值为，
所以面积的最小值为，故C错误；
D项：由题意得为锐角，
则取最小值时，取最大值，
也即与圆相切时，
此时，
故，故D正确.
故选：BD.
  
【点睛】关键点点睛：以点为原点建立平面直角坐标系，求出动点的轨迹方程，是解决本题的关键.
7．（2023·海南省直辖县级单位·文昌中学校考模拟预测）（多选）已知圆和圆的交点为，直线：与圆交于两点，则下列结论正确的是（    ）
A．直线的方程为
B．圆上存在两点和，使得
C．圆上的点到直线的最大距离为
D．若，则或
【答案】CD
【分析】将两圆方程化为标准式，即可得到圆心坐标与半径，从而判断两圆相交，将两圆方程作差得到公共弦方程，即可判断A，再利用弦长公式判断B，求出到的距离，即可判断C，圆心到直线的距离为，即可得到方程，判断D.
【详解】圆的标准方程为，圆心为，半径为，
圆的标准方程为，圆心为，半径为，
所以，
所以两圆相交，所以将两圆的方程作差可得，
即直线的方程为，故A错误；
圆心到直线的距离为，所以，
对于圆上的任意两点，，故B错误；
圆上的点到直线的距离的最大值为，故C正确；
因为，所以圆心到直线的距离为，所以，
故或，故D正确.
  
故选：CD

1．（2023·甘肃酒泉·统考三模）若直线分别与轴，轴交于，两点，动点在圆上，则面积的取值范围是（    ）
A． B． C． D．
【答案】C
【分析】先求得点A、点B的坐标，进而求得，再求出圆上的点P到直线距离的最值，代入三角形面积公式即可求得结果.
【详解】如图所示，
  
因为直线与坐标轴的交点，，则，
圆的圆心C为，半径为，
则圆心到直线的距离为，
所以圆上的点P到直线的距离的最小值为，最大距离为，
所以面积的最小值为，最大值为，
即面积的取值范围为.
故选：C.
2．（2023·浙江嘉兴·统考模拟预测）已知点是直线：和：的交点，点是圆：上的动点，则的最大值是（    ）
A． B． C． D．
【答案】B
【分析】根据题意分析可知点的轨迹是以的中点，半径的圆，结合圆的性质运算求解.
【详解】因为直线：，即，
令，解得，可知直线过定点，
同理可知：直线过定点，
又因为，可知，
所以直线与直线的交点的轨迹是以的中点，半径的圆，
因为圆的圆心，半径，
所以的最大值是.
故选：B.
3．（2023·福建泉州·泉州五中校考模拟预测）已知复数满足，则的最大值为（    ）
A． B．2 C． D．3
【答案】C
【分析】设，得出的关系，结合其几何意义求解最值.
【详解】设，
因为，
所以，
因为，
所以相当于圆上的点到点距离，
所以的最大值为圆心到点距离与圆的半径的和，即.
故选：C.
  
4．（2023·云南昭通·校联考模拟预测）已知，，点为圆上任意一点，则面积的最大值为（    ）
A．5 B． C． D．
【答案】D
【分析】根据给定条件，求出直线的方程，再求出点P到直线距离的最大值作答.
【详解】圆的圆心，半径，直线的方程为：，
于是点到直线：的距离，而点在圆上，
因此点到直线距离的最大值为，又，
所以面积的最大值为.
故选：D
  

5．（2023·海南省直辖县级单位·嘉积中学校考三模）已知，是圆：上的两个不同的点，若，则的取值范围为 ．
【答案】
【分析】为和到直线距离之和的倍，是的中点到直线距离的倍，利用点轨迹，求取值范围.
【详解】由题知，圆的圆心坐标，半径为2，因为，所以．
设为的中点，所以，所以点的轨迹方程为．
点的轨迹是以为圆心半径为的圆.
设点，，到直线的距离分别为，，，

所以，，，
所以．
因为点到直线的距离为，所以，
即，所以．
所以的取值范围为．
故答案为：
【点睛】思路点睛：
利用的几何意义，问题转化为为和到直线距离之和，再转化为的中点到直线距离，由点轨迹是圆，可求取值范围.
6．（2023·辽宁抚顺·校考模拟预测）（多选）如图所示，该曲线W是由4个圆：，，，的一部分所构成，则下列叙述正确的是（    ）
  
A．曲线W围成的封闭图形面积为4+2π
B．若圆与曲线W有8个交点，则
C．与的公切线方程为
D．曲线W上的点到直线的距离的最小值为4
【答案】ACD
【分析】A选项可将曲线W围成的封闭图形可分割为一个边长为2的正方形和四个半径为1的相同的半圆，即可判断；
B选项可直接由图讨论判断对错；
C选项可由圆心到直线的距离等于半径，求出公切线；
D选项可先找到，的公切线方程为，曲线W上的点到直线的距离的最小值即为平行线间的距离.
【详解】曲线W围成的封闭图形可分割为一个边长为2的正方形和四个半径为1的相同的半圆，
所以其面积为，故A选项正确.
当时，交点为B，D，F，H；当时，交点为A，C，E，G；
当或时，没有交点；当时，交点个数为8，故B选项错误.
设与的公切线方程为，
由直线和圆相切的条件可得，
解得，（舍去），
则其公切线方程为，即，故C选项正确.
同理可得，的公切线方程为，
则两平行线的距离，故D选项正确.
故选：ACD.
7．（2023·吉林长春·东北师大附中校考模拟预测）（多选）已知圆的圆心在直线上，且与相切于点，过点作圆的两条互相垂直的弦，记线段的中点分别为，则下列结论正确的是（    ）
A．圆的方程为 B．四边形面积的最大值为
C．弦的长度的取值范围为 D．直线恒过定点
【答案】ACD
【分析】利用待定系数法求出圆E的方程，判断A；根据圆的几何性质表示出四边形面积，结合二次函数知识求得其最大值，判断B；利用圆的几何性质可求得弦的长度的取值范围，判断C；结合四边形为矩形，可判断D.
【详解】由题意可设圆心为，半径为，
故，解得，则，
故圆的方程为，A正确；
  
连接,则,
设,则,则，
故，
所以，
当时，四边形面积取到最大值，B错误；
当弦过圆心时最长，最大值为4；
当弦时最短，最小值为，
即弦的长度的取值范围为，C正确；
由题意知，，
故四边形为矩形，则为矩形的对角线，二者互相平分，
而，故过的中点，D正确，
故选：ACD


【基础过关】
一、单选题
1．（2023·北京海淀·校考三模）若直线是圆的一条对称轴，则（    ）
A． B．1 C． D．
【答案】A
【分析】首先得到圆心坐标，即可得到圆心在直线上，从而求出参数的值.
【详解】圆的圆心为，因为直线是圆的一条对称轴，
所以圆心在直线上，所以，解得.
故选：A
2．（2023·北京通州·统考三模）过直线上的一点作圆的两条切线，，切点分别为，当直线，关于对称时，线段的长为（    ）
A．4 B． C． D．2
【答案】C
【分析】根据题意画出图形，观察图形可知圆心与点的连线垂直于直线，利用这一关系即可得到切线的长.
【详解】如图所示，圆心为，连接，
  
因为直线，关于对称，所以垂直于直线，
故，而，
所以.
故选：C
3．（2023·新疆喀什·校考模拟预测）已知圆，直线，则圆C与直线l（    ）
A．相交 B．相切 C．相离 D．相交且直线过圆C的圆心
【答案】B
【分析】根据题意只需判断圆心到直线的距离与半径比较大小即可判断．
【详解】由可得，
故圆心，半径，
则圆心到直线的距离，
故直线与圆C相切．
故选：B
4．（2023·山东济宁·嘉祥县第一中学统考三模）若直线与圆：相交于，两点，则的最小值为（    ）
A． B． C． D．
【答案】B
【分析】求出直线过的定点并判断与圆的位置关系，再求出垂直于经过该定点的圆的直径的弦长作答.
【详解】直线，即恒过定点，
而，即点在圆内，
因此当且仅当时，最小，
而圆的圆心，半径，，
所以.
故选：B
  
5．（2023·河北·校联考一模）直线与圆相切，则的最大值为（    ）
A．16 B．25 C．49 D．81
【答案】C
【分析】利用圆与直线的位置关系得出的方程，根据方程分析利用表示的几何意义求解即可.
【详解】由直线与圆相切可得：
圆心到直线的距离等于圆的半径，
即，
故，即点在圆O上，
的几何意义为圆上的点与点之间距离的平方，
由圆心为，
因为，
所以点在圆外，
所以点到点的距离的最大值为圆心到的距离与圆半径之和，
即，
所以的最大值为.
故选：C.

二、填空题
6．（2023·广东深圳·校考二模）过点且被圆所截得的弦长为的直线的方程为 .
【答案】
【分析】首先将圆的方程配成标准式，即可得到圆心坐标与半径，由弦长求出圆心到直线的距离，分析可得直线的斜率存在，设直线方程为，利用点到直线的距离公式求出，即可得解.
【详解】圆，即，
圆心为，半径，
若弦长，则圆心到直线的距离，
显然直线的斜率存在，设直线方程为，即，
所以，解得，所以直线方程为.
故答案为：
7．（2023·浙江·校联考模拟预测）已知圆和圆，则过点且与都相切的直线方程为 .（写出一条即可）
【答案】或（写出一条即可）
【分析】由直线与圆的位置关系通过几何法计算即可.
【详解】若过M的切线斜率不存在，即为，此时显然与两圆都相切；
若过M的切线斜率存在，不妨设为，则到的距离分别为，
即.
综上过M与两圆都相切的直线为：或
故答案为：或（写出一个即可）
8．（2023·上海普陀·曹杨二中校考模拟预测）抛物线的准线与圆相交于A、B两点，则 ．
【答案】2
【分析】首先求抛物线的准线方程，再根据直线与圆相交的弦长公式，即可求解.
【详解】的准线方程为，圆心到直线的距离为，
所以弦长.
故答案为：2
9．（2023·安徽合肥·合肥市第六中学校考模拟预测）圆心在直线上，且与直线相切于点的圆的标准方程为 ．
【答案】
【分析】设圆心坐标为，利用点到直线距离公式和两点距离公式求解即可.
【详解】设圆心坐标为，因为圆与直线相切于点，
所以，可得：，
解得，
所以所求圆的圆心为，半径，
所以所求圆的方程为.
故答案为：.
10．（2023·陕西安康·陕西省安康中学校考模拟预测）圆心在直线上，且与直线相切的一个圆的方程为 .
【答案】（答案不唯一）
【分析】依题意可得直线与直线平行，则两平行线之间的距离即为圆的半径，再取一个点确定圆心，即可得到圆的方程.
【详解】因为直线与直线平行，
设圆心坐标为，因为圆心到直线的距离等于圆的半径r，
所以，取，则圆的方程为.
故答案为：（答案不唯一）

【能力提升】
一、单选题
1．（2023·山东泰安·统考模拟预测）已知直线与圆，过直线上的任意一点向圆引切线，设切点为，若线段长度的最小值为，则实数的值是（    ）
A． B． C． D．
【答案】A
【分析】设，则，可得，而的最小值是圆心到直线的距离，然后列方程可求出实数m的值.
【详解】圆，设，
则，则，，
则，所以圆心到直线的距离是，
，得，．
故选：A．
2．（2023·广东广州·华南师大附中校考三模）在平面直角坐标系中，若抛物线的准线与圆相切于点，直线与抛物线切于点，点在圆上，则的取值范围为（    ）
A． B．
C． D．
【答案】C
【分析】根据抛物线的准线与圆相切可求得的值，可得出抛物线的方程，求出点的坐标，设出直线的方程，将直线的方程与抛物线的方程联立，求出点的坐标，设点的坐标为，利用平面向量数量积的坐标运算结合三角恒等变换可求得的取值范围.
【详解】抛物线的准线方程为，
  
圆的圆心为，半径为，直线与圆相切，则，
因为，解得，所以，抛物线的方程为，
故抛物线的准线与圆相切于点，
若直线与轴重合，则直线与抛物线不相切，不合乎题意，
设直线的方程为，联立可得，
则，解得，
不妨设点在第一象限，则，则有，解得，
此时，即点，所以，，
因为点在圆上，设点，则，
所以，.
故选：C.
3．（2023·广东珠海·珠海市第一中学校考模拟预测）已知圆，点，若圆M上存在两点B，C，使得是等边三角形，则实数的取值范围是（    ）
A． B． C． D．
【答案】D
【分析】条件可转化为存在点B使得，然后过点A作圆M的切线，切点为T，连接MT，则，然后可求出的范围，然后可得答案.
【详解】由题知，圆M和正组成的图形关于直线AM对称，
  
若存在点B，C满足题意等价于存在点B使得，
过点A作圆M的切线，切点为T，连接MT，则，
又，所以，
则，解得．
故选：D
4．（2023·浙江·模拟预测）已知圆和点，由圆外一点向圆引切线，切点分别为，若，则的最小值是（    ）
A． B． C． D．
【答案】C
【分析】设，利用可得，再由利用配方法可得答案.
【详解】设，连接，则，可得，
所以，
即，可得，
所以，
当时，.
故选：C.
  

二、多选题
5．（2023·山东烟台·统考三模）已知点为直线与轴交点，为圆上的一动点，点，则（    ）
A．取得最小值时， B．与圆相切时，
C．当时， D．的最大值为
【答案】ABD
【分析】A：取得最小值时位于即轴上，根据三角形面积公式可得.
B：直接在直角三角形利用勾股定理可得.
C：运用向量的坐标表示和对于坐标运算可得.
D：根据正弦定理，将求的最大值转化为求外接圆半径最小，
此时，外接圆与圆相内切，根据内切半径差等于圆心距可得外接圆半径，进而可得.
【详解】因，令，得，
故，
，圆心，半径
选项A：
  
如图，根据圆的性质当位于轴上时，取得最小值，
此时，故A正确；
选项B：
  
当与圆相切时，
，
故B正确；
选项C：
  
设，
则，，
当时，，
故，
又，
得，
，，

若，则，
又得，，，
此时，
这与点在圆上矛盾，故C错误；
选项D：
  
设外接圆圆心为，半径为
由题意可得在中垂线上，可设其坐标为，
则，，
由正弦定理知，所以，
当最小，即外接圆与圆相内切时，的最大值，
此时圆心距等于两圆半径之差，则
，
两边同时平方可得，
，故D正确.
故选：ABD.
6．（2023·湖南·校联考模拟预测）已知直线：，：，圆C：，下列说法正确的是（    ）
A．若经过圆心C，则
B．直线与圆C相离
C．若，且它们之间的距离为，则
D．若，与圆C相交于M，N，则
【答案】AC
【分析】将圆心代入直线的方程，求得k，判断A；求得直线过圆内一定点，判断B；利用平行线间的距离公式可判断C；根据圆的几何性质可求得，判断D.
【详解】对于A，因为圆心在直线上，所以，解得，A正确；
对于B，因为直线恒过点，且，
即点在圆C内，所以与圆C相交，B错误；
对于C，因为，则，
故与之间的距离，所以，C正确；
对于D，时，直线：，即，
因为圆心到直线的距离，
所以，D错误，
故选：AC.
7．（2023·辽宁沈阳·沈阳二中校考模拟预测）已知，过点作圆的切线，切点分别为，则下列命题中真命题是（    ）
A．
B．直线的方程为
C．圆与共有4条公切线
D．若过点的直线与交于两点，则当面积最大时，.
【答案】ABD
【分析】由圆的方程确定圆心坐标和半径，结合切线性质求，判断A，
求过点的圆的方程，再求其与圆的公共弦可得直线的方程，判断B，
判断圆与圆的位置关系，判断C，
结合三角形面积公式求的面积的最大值，求，判断D，
【详解】因为圆的方程为，
所以圆心的坐标为，半径为，所以，
又，所以，
由已知，
所以，A正确，
因为，
所以点四点共圆，且圆心为的中点，
线段的中点坐标为，
所以圆的方程为，即，
因为，所以圆与圆相交，
又圆的方程可化为
所以圆与圆的公共弦方程为，
故直线的方程为，B正确，
  
圆的圆心的坐标为，半径为，
因为，，
所以圆与圆相交，故两圆只有2条公切线，C错误；
设，则，
的面积，
所以当时，的面积取最大值，最大值为，此时，D正确.
故选：ABD.
  
8．（2023·辽宁·辽宁实验中学校考模拟预测）已知点M，N在圆O：上运动，点，且，Q为线段M，N的中点，则（    ）
A．过点P有且只有一条直线与圆O相切
B．
C．点Q在直线上运动
D．的最大值为
【答案】BD
【分析】首先判断与圆的位置关系，数形结合判断A、B；再应用两点距离、中点公式及已知求得在直线上判断C；由几何法求得，结合点线距离求的最大值.
【详解】由，故在圆外，故过点P有两条直线与圆O相切，A错；
  
由为线段的中点，为圆的弦，故，B对；
由，又都在圆上，
所以，即，而，，
所以，即点在直线上，C错；
由，当最小时，最大，
而最小值为到的距离为，此时Q在圆的内部，
所以，D对.
故选：BD
9．（2023·广东广州·广州市从化区从化中学校考模拟预测）设，过定点的直线与过定点的直线相交于点，线段是圆的一条动弦，且，给出下列四个结论：其中所有正确结论的序号是（    ）
A．一定垂直
B．的最大值为4
C．点的轨迹方程为
D．的最小值为
【答案】AB
【分析】A选项，根据两直线垂直满足的关系式进行判断；B选项，求出和，由⊥，得到，再结合基本不等式得到答案；C选项，分析得到，点的轨迹为以为直径的圆，求出轨迹方程；D选项，设的中点为，求出，得到点轨迹方程，进而得到的最小值为圆心距减去两半径，结合求出答案.
【详解】A选项，因为，所以一定垂直，A正确；
B选项，变形得到，从而，
变形得到，从而，
由⊥，由勾股定理得，
由基本不等式可得，故，
当且仅当时，等号成立，故B正确；
C选项，由B可知，点的轨迹为以为直径的圆，其中线段的中点坐标为，半径为，
故轨迹方程为（不包含点），C错误；
D选项，的圆心为，半径为2，
设的中点为，由垂径定理得，
  
故点的轨迹方程为，
因为点轨迹方程为，
则的最小值为圆心距减去两半径，即，
其中，
所以的最小值为，D错误.
故选：AB

三、填空题
10．（2023·江苏·金陵中学校联考三模）已知抛物线：，圆：，点M的坐标为，分别为、上的动点，且满足，则点的横坐标的取值范围是 .
【答案】
【分析】利用抛物线的定义和圆的性质得到，转化为，即可解得.
【详解】因为抛物线：的焦点，准线：，所以圆心即为抛物线的焦点F，设，
∴，∴.
∵，
∴，，
∴，∴.
故答案为：

【真题感知】
一、单选题
1．（山东·统考高考真题）已知圆心为的圆与轴相切，则该圆的标准方程是（    ）
A． B．
C． D．
【答案】B
【分析】圆的圆心为，半径为，得到圆方程.
【详解】根据题意知圆心为，半径为，故圆方程为：.
故选：B.
2．（北京·统考高考真题）已知半径为1的圆经过点，则其圆心到原点的距离的最小值为（    ）．
A．4 B．5 C．6 D．7
【答案】A
【分析】求出圆心的轨迹方程后，根据圆心到原点的距离减去半径1可得答案.
【详解】设圆心，则，
化简得，
所以圆心的轨迹是以为圆心，1为半径的圆，

所以，所以，
当且仅当在线段上时取得等号，
故选：A.
【点睛】本题考查了圆的标准方程，属于基础题.
3．（2022·北京·统考高考真题）若直线是圆的一条对称轴，则（    ）
A． B． C．1 D．
【答案】A
【分析】若直线是圆的对称轴，则直线过圆心，将圆心代入直线计算求解．
【详解】由题可知圆心为，因为直线是圆的对称轴，所以圆心在直线上，即，解得．
故选：A．

4．（全国·统考高考真题）已知⊙M：，直线：，为上的动点，过点作⊙M的切线，切点为，当最小时，直线的方程为（    ）
A． B． C． D．
【答案】D
【分析】由题意可判断直线与圆相离，根据圆的知识可知，四点共圆，且，根据 可知，当直线时，最小，求出以 为直径的圆的方程，根据圆系的知识即可求出直线的方程．
【详解】圆的方程可化为，点 到直线的距离为，所以直线 与圆相离．
依圆的知识可知，四点四点共圆，且，所以，而 ，
当直线时，， ，此时最小．
∴即 ，由解得， ．
所以以为直径的圆的方程为，即 ，
两圆的方程相减可得：，即为直线的方程．
故选：D.
【点睛】本题主要考查直线与圆，圆与圆的位置关系的应用，以及圆的几何性质的应用，意在考查学生的转化能力和数学运算能力，属于中档题．
5．（全国·统考高考真题）已知圆，过点（1，2）的直线被该圆所截得的弦的长度的最小值为（    ）
A．1 B．2
C．3 D．4
【答案】B
【分析】当直线和圆心与点的连线垂直时，所求的弦长最短，即可得出结论.
【详解】圆化为，所以圆心坐标为，半径为，
设，当过点的直线和直线垂直时，圆心到过点的直线的距离最大，所求的弦长最短，此时
根据弦长公式得最小值为.
故选：B.
【点睛】本题考查圆的简单几何性质，以及几何法求弦长，属于基础题.
6．（全国·统考高考真题）若直线l与曲线y=和x2+y2=都相切，则l的方程为（    ）
A．y=2x+1 B．y=2x+ C．y=x+1 D．y=x+
【答案】D
【分析】根据导数的几何意义设出直线的方程，再由直线与圆相切的性质，即可得出答案.
【详解】设直线在曲线上的切点为，则，
函数的导数为，则直线的斜率，
设直线的方程为，即，
由于直线与圆相切，则，
两边平方并整理得，解得，（舍），
则直线的方程为，即.
故选：D.
【点睛】本题主要考查了导数的几何意义的应用以及直线与圆的位置的应用，属于中档题.
7．（2023·全国·统考高考真题）已知双曲线的离心率为，C的一条渐近线与圆交于A，B两点，则（    ）
A． B． C． D．
【答案】D
【分析】根据离心率得出双曲线渐近线方程，再由圆心到直线的距离及圆半径可求弦长.
【详解】由，则，
解得，
所以双曲线的一条渐近线不妨取，
则圆心到渐近线的距离，
所以弦长.
故选：D

二、多选题
8．（2021·全国·统考高考真题）已知点在圆上，点、，则（    ）
A．点到直线的距离小于
B．点到直线的距离大于
C．当最小时，
D．当最大时，
【答案】ACD
【分析】计算出圆心到直线的距离，可得出点到直线的距离的取值范围，可判断AB选项的正误；分析可知，当最大或最小时，与圆相切，利用勾股定理可判断CD选项的正误.
【详解】圆的圆心为，半径为，
直线的方程为，即，
圆心到直线的距离为，
所以，点到直线的距离的最小值为，最大值为，A选项正确，B选项错误；
如下图所示：

当最大或最小时，与圆相切，连接、，可知，
，，由勾股定理可得，CD选项正确.
故选：ACD.
【点睛】结论点睛：若直线与半径为的圆相离，圆心到直线的距离为，则圆上一点到直线的距离的取值范围是.
9．（海南·高考真题）已知曲线.（    ）
A．若m>n>0，则C是椭圆，其焦点在y轴上
B．若m=n>0，则C是圆，其半径为
C．若mn0，则C是两条直线
【答案】ACD
【分析】结合选项进行逐项分析求解，时表示椭圆，时表示圆，时表示双曲线，时表示两条直线.
【详解】对于A，若，则可化为，
因为，所以，
即曲线表示焦点在轴上的椭圆，故A正确；
对于B，若，则可化为，
此时曲线表示圆心在原点，半径为的圆，故B不正确；
对于C，若，则可化为，
此时曲线表示双曲线，
由可得，故C正确；
对于D，若，则可化为，
，此时曲线表示平行于轴的两条直线，故D正确；
故选：ACD.
【点睛】本题主要考查曲线方程的特征，熟知常见曲线方程之间的区别是求解的关键，侧重考查数学运算的核心素养.

三、填空题
10．（2021·天津·统考高考真题）若斜率为的直线与轴交于点，与圆相切于点，则 ．
【答案】
【分析】设直线的方程为，则点，利用直线与圆相切求出的值，求出，利用勾股定理可求得.
【详解】设直线的方程为，则点，
由于直线与圆相切，且圆心为，半径为，
则，解得或，所以，
因为，故.
故答案为：.
11．（2022·全国·统考高考真题）过四点中的三点的一个圆的方程为 ．
【答案】或或或．
【分析】方法一：设圆的方程为，根据所选点的坐标，得到方程组，解得即可；
【详解】[方法一]：圆的一般方程
依题意设圆的方程为，
（1）若过，，，则，解得，
所以圆的方程为，即；
（2）若过，，，则，解得，
所以圆的方程为，即；
（3）若过，，，则，解得，
所以圆的方程为，即；
（4）若过，，，则，解得，所以圆的方程为，即；
故答案为：或 或 或．
[方法二]：【最优解】圆的标准方程（三点中的两条中垂线的交点为圆心）
设
（1）若圆过三点，圆心在直线，设圆心坐标为，
则，所以圆的方程为；
（2）若圆过三点， 设圆心坐标为，则，所以圆的方程为；
（3）若圆过 三点，则线段的中垂线方程为，线段 的中垂线方程 为，联立得 ，所以圆的方程为；
（4）若圆过三点，则线段的中垂线方程为， 线段中垂线方程为 ，联立得，所以圆的方程为．
故答案为：或 或 或．
【整体点评】方法一；利用圆过三个点，设圆的一般方程，解三元一次方程组，思想简单，运算稍繁；
方法二；利用圆的几何性质，先求出圆心再求半径，运算稍简洁，是该题的最优解．

12．（2022·全国·统考高考真题）若双曲线的渐近线与圆相切，则 ．
【答案】
【分析】首先求出双曲线的渐近线方程，再将圆的方程化为标准式，即可得到圆心坐标与半径，依题意圆心到直线的距离等于圆的半径，即可得到方程，解得即可．
【详解】解：双曲线的渐近线为，即，
不妨取，圆，即，所以圆心为，半径，
依题意圆心到渐近线的距离，
解得或（舍去）．
故答案为：．

13．（2023·全国·统考高考真题）已知直线与交于A，B两点，写出满足“面积为”的m的一个值 ．
【答案】（中任意一个皆可以）
【分析】根据直线与圆的位置关系，求出弦长，以及点到直线的距离，结合面积公式即可解出．
【详解】设点到直线的距离为，由弦长公式得，
所以，解得：或，
由，所以或，解得：或．
故答案为：（中任意一个皆可以）．