





选择性必修 第三册第六章 计数原理6.2 排列与组合备课课件ppt
展开理解排列、排列数的概念
能正确写出一些简单问题的所有排列(列举、树状图、表格)能够求出排列数
应用排列与排列数的知识解决简单的实际问题
一般地,从n个不同元素中取出m(m≤n)个元素,并按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列(arrangement).
2.排列问题的判断方法:
(1)元素的无重复性(2)元素的有序性
判断的关键:变换元素的位置,看结果是否发生变化,有变化是有序,无变化就是无序.
引入:通过上节课中的问题1和问题2,我们学习了排列的定义,并利用分步乘法计数原理或列举法计算排列的个数,但是如果元素增多,这样的表达和计算方法会显得繁琐冗长.简化一直是数学的追求,能进一步实现对排列问题的简化运算吗?
问题1 我们现在要创设一个符号简化表示“从 n 个不同元素中取出 m ( m ≤ n )个元素,并按照一定的顺序排列成一列的所有不同排列的个数”,这个符号需考虑几个要素?
三个要素:被选取范围元素个数: n 取出元素个数:m ( m ≤ n ),顺序
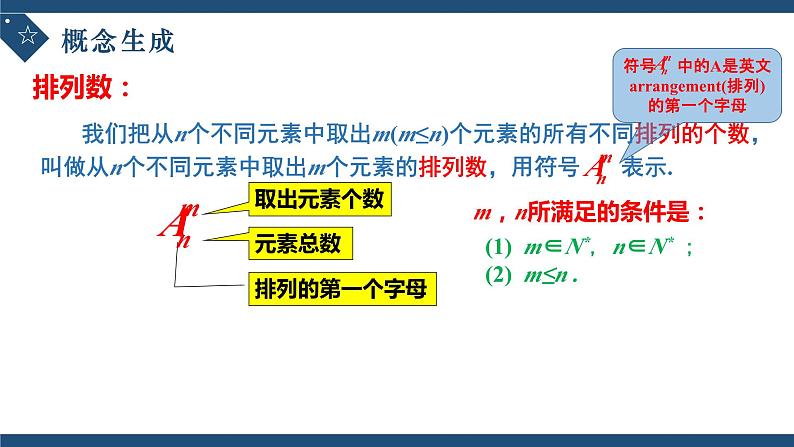
m,n所满足的条件是:
(1) m∈N*,n∈N* ;(2) m≤n .
追问2 “从n个不同元素中取出m(m≤n)个元素,并按照一定的顺序排成一列”与“从n个不同元素中取出m(m≤n)个元素的排列数”是同一回事吗?
问题1是从3个不同元素中任取2个元素的排列为3×2=6 ,可记作:
问题2是从4个不同元素中任取3个元素的排列数为4×3×2=24 ,可记作:
追问1 你能用排列数符号表示上节课中的问题1和问题2吗?
排列是指从n个不同元素中取出m(m≤n)个元素,排成一列的具体排法,也就是完成一件事的一种方法,它不是数; 排列数是指从n个不同元素中取出m(m≤n)个元素,排成一列所有排列的个数,它是一个数.
我们先从特殊情况开始探究,思考从n个不同元素中任取2个元素的排列数 是多少? 又是多少?进而归纳 是多少?
探究 研究了排列数的符号表达,是否有排列数公式便捷的求出排列个数从n个不同元素中取出m个元素的排列数 (m≤n)是多少?
问题2 观察排列数公式的结构,回答下列问题:(1)观察公式的右边,有什么特点?共有几个因数?(2)比较n与m的大小关系,并说明公式右边的最后一个因数有什么特点?(3)若m=n时, 的表达式有什么特点?
公式中是m个连续正整数的连乘积,从n开始每项逐次减1
最小因数是(n-m+1)而不是(n-m).
1. 全排列:从n个不同素中取出n个元素的一个排列称为n个不同 元素的一个全排列 .
解:根据排列数公式,可得:
追问 观察例3的运算结果,你有什么发现?能推广到一般情况吗?
追问 你能否对它进行证明呢?
因此,排列数公式还可以写成:
排列数公式的应用: 连乘形式一般用于的计算, 阶乘形式用于化简或证明.
3. 一个火车站有8股岔道,如果每股道只能停放1列火车,现要停放4列不同的火车,共有多少种不同的停放方法?
例4 用0~9这10个数字,可以组成多少个没有重复数字的三位数?
分析:在0~9这10个数字中,因为0不能在百位上,而其他9个数字可以在任意数位上,因此0是一个特殊的元素. 一般地,我们可以从特殊元素的位置入手来考虑问题。
解法1:由于三位数的百位上的数字不能是0,所以可以分两步完成:
根据分步乘法计数原理,所求的三位数的个数为:
解法2:符合条件的三位数可以分成三类:
它们的差就是用这10个数组成的没有重复数字的三位数的个数
带有限制条件的排列问题:“特殊”优先原则
以位置为主,优先考虑特殊位置
以元素为主,优先考虑特殊元素
先不考虑限制条件,计算出来所有排列数,再从中减去全部不符合条件的排列数,从而得出符合条件的排列数
变式1 用0到9这十个数字,可以组成多少个没有重复数字的三位数且是偶数?
变式2 用0到9这十个数字,可以组成多少个没有重复数字的三位数且是奇数?
排列数公式的阶乘形式:
(1) 若三个女孩要站在一起,有多少种不同的排法?
例题 七个家庭一起外出旅游,若其中四家是男孩,三家是女孩,现将这七个小孩站成一排照相留念.
(2) 若三个女孩要站在一起,四个男孩也要站在一起,有多少种不同的排法?
(3) 若三个女孩互不相邻,有多少种不同的排法?
(4) 若三个女孩互不相邻,四个男孩也互不相邻,有多少种不同的排法?
(6) 若前排站三人,后排站四人,其中的A, B两小孩必须站前排且相邻,有多少种不同的排法?
(5) 若其中的A小孩必须站在B小孩的左边,有多少种不同的排法?
(5) A在B左边的一种排法必对应着A在B右边的一种排法,而在全排列中,A在B左边与A在B右边的排法数相等,因此不同的排法有
变式 5个人站成一排: (l) 共有多少种不同的排法? (2) 其中甲必须站在中间有多少种不同排法? (3) 其中甲、乙两人必须相邻有多少种不同的排法? (4) 其中甲、乙两人不相邻有多少种不同的排法? (5) 其中甲、乙两人不站排头和排尾有多少种不同的排法? (6) 其中甲不站排头,乙不站排尾有多少种不同的排法?
解:(1)由于没有条件限制,5个人可作全排列,所以不同的排法共有
(2)由于甲的位置已确定,其余4人可任意排列,所以不同的排法有
(6)可将问题分为两类:
① 甲站在排尾,其余的人可全排列,
② 甲既不站在排尾也不站排头,乙不站排尾,其余的人可全排列,
变式 5个人站成一排: (6) 其中甲不站排头,乙不站排尾有多少种不同的排法?
人教A版 (2019)选择性必修 第三册6.2 排列与组合教学课件ppt: 这是一份人教A版 (2019)选择性必修 第三册6.2 排列与组合教学课件ppt,共24页。PPT课件主要包含了理解排列数的概念等内容,欢迎下载使用。
选择性必修 第三册第六章 计数原理6.2 排列与组合课文内容课件ppt: 这是一份选择性必修 第三册第六章 计数原理6.2 排列与组合课文内容课件ppt,共43页。PPT课件主要包含了学习目标等内容,欢迎下载使用。
高中数学人教A版 (2019)选择性必修 第三册6.2 排列与组合优秀课件ppt: 这是一份高中数学人教A版 (2019)选择性必修 第三册6.2 排列与组合优秀课件ppt,文件包含621-622排列与排列数课件-人教A版选择性必修第三册pptx、621-622排列与排列数导学案-人教A版选择性必修第三册docx、621-622排列与排列数教学设计-人教A版选择性必修第三册docx等3份课件配套教学资源,其中PPT共0页, 欢迎下载使用。














