数学选择性必修 第三册6.2 排列与组合图文课件ppt

这是一份数学选择性必修 第三册6.2 排列与组合图文课件ppt，共43页。PPT课件主要包含了学习目标等内容，欢迎下载使用。

类比与理解组合数的概念
能利用计数原理推导组合数公式
能用组合数的知识与公式求解相关问题
2.判断一个计数问题是排列问题还是组合问题的方法：
若交换某两个元素的位置对结果有影响，则是排列问题，即排列问题与选取的顺序有关.
若交换任意两个元素的位置对结果没有影响，则是组合问题，即组合问题与选取的顺序无关.
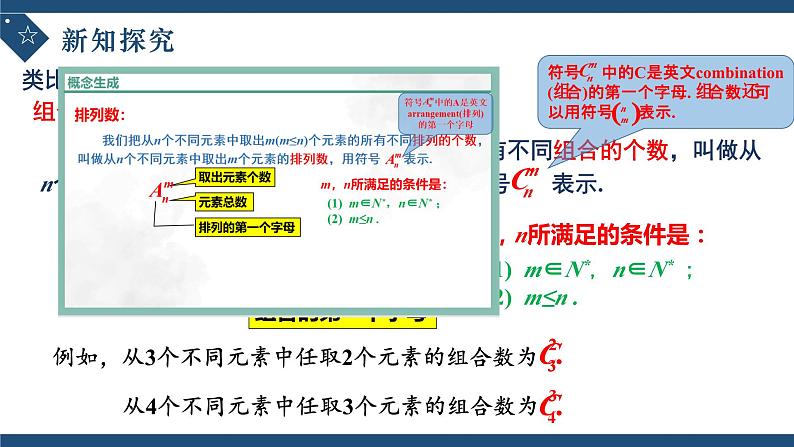
一般地，从n个不同元素中取出m(m≤n)个元素并成一组，叫做从n个不同元素中取出m个元素的一个组合．
类比排列数，我们引进组合数概念：
m，n所满足的条件是：
(1) m∈N*，n∈N* ；(2) m≤n .
例如，从3个不同元素中任取2个元素的组合数为
从4个不同元素中任取3个元素的组合数为
回顾：从甲、乙、丙3名同学中选出2名参加一项活动，有多少种不同的选法？
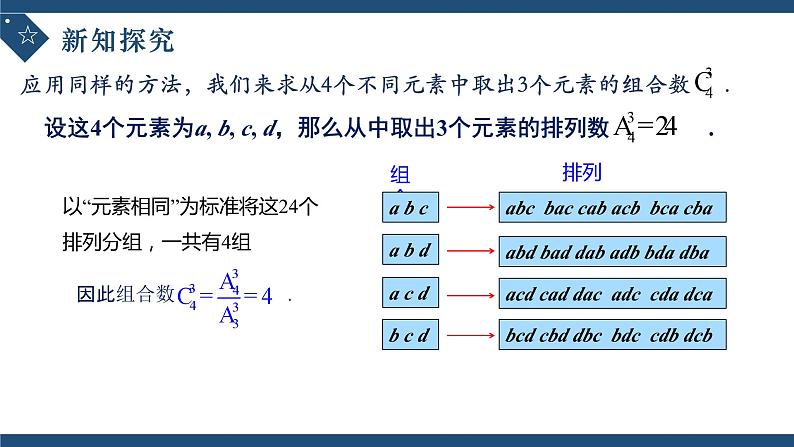
应用同样的方法，我们来求从4个不同元素中取出3个元素的组合数 .
设这4个元素为a, b, c, d，那么从中取出3个元素的排列数 .
以“元素相同”为标准将这24个排列分组，一共有4组
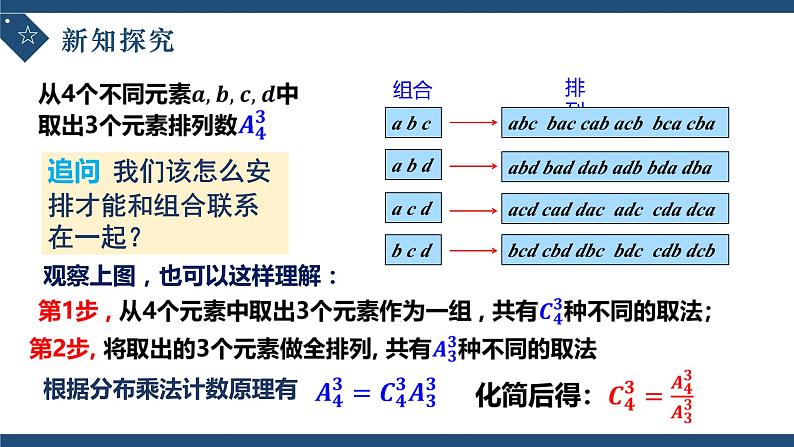
观察上图，也可以这样理解：
根据分布乘法计数原理有
所以上面的公式还可以写成
思考 此关系是否具有一般性？
问题3 对于组合数的这个性质你能给出证明与解释吗？
该性质反映了组合数的对称性. 其组合意义是从n个不同的元素中任取m个元素的组合与任取(n-m)个元素的组合是一一对应(一种取法对应一种剩法). 因为从n个不同元素中取出m个元素后，就剩下(n-m)个元素，因此从n个不同元素中取出m个元素的方法，与从n个不同元素中取出(n-m)个元素的方法是一一对应的，因此取法是一样多的，就是说从n个不同元素中取出m个元素的每一个组合，都对应着从n个不同元素中取出(n-m)个元素的唯一的一个组合，反过来也一样. 即从n个不同元素中取出m个元素的组合数 等于从n个不同元素中取出(n-m)个元素的组合数 ，也就是 .
该性质也可以根据组合数的定义与分类加法计数原理直接得出，在确定从(n+1)个不同元素中取m个元素的方法时，对于某一元素，只存在着取与不取两种可能. 如果取这一元素，则需从剩下的n个元素中再取出(m-1)个元素，所以共有 种取法；如果不取这一元素，则需从剩下的n个元素中再取出m个元素，所以共有 种取法. 由分类加法计数原理，得 .
追问：你有什么发现和猜想？
例3 在100件产品中，有98件合格品，2件次品. 从这100件产品中任意抽出3件.(1)有多少种不同的抽法？(2)抽出的3件中恰好有1件是次品的抽法有多少种？(3)抽出的3件中至少有1件是次品的抽法有多少种？
(1) 所有的不同抽法种数，就是从100件产品中抽出3件的组合数，所以抽法种数为
从100件产品抽出的3件中至少有1件是次品，包括有1件次品和有2件次品两种情况，因此根据分类加法计数原理，抽出的3件中至少有1件是次品的抽法种数为
(3)解1(直接法)：
抽出的3 件中至少有1件是次品的抽法种数，就是从100件产品中抽出3件的抽法种数减去3件都是合格品的抽法种数，即
变式：把(3)中的“至少”改为“至多”， 则抽法有多少种?
“至少”“至多”的问题，通常用分类法或间接法求解
3. 有政治、历史、地理、物理、化学、生物这6门学科的学业水平考试成绩，现要从中选3门考试成绩. (1) 共有多少种不同的选法? (2) 如果物理和化学恰有1门被选，那么共有多少种不同的选法? (3) 如果物理和化学至少有1门被选，那么共有多少种不同的选法?
1.组合数的定义和表示