

2022-2023学年江苏省无锡市市北高级中学高一(上)期中数学试卷
展开
这是一份2022-2023学年江苏省无锡市市北高级中学高一(上)期中数学试卷,共15页。试卷主要包含了单选择题,多项选择题,填空题,解答题等内容,欢迎下载使用。
1.(5分)已知R是实数集,集合A={x∈Z||x|<2},B={x|2x﹣1≥0},则A∩(∁RB)=( )
A.B.{1}C.{﹣1,0}D.
2.(5分)已知x≠0,则“”是“x>2022”的( )条件
A.必要不充分B.充分不必要
C.充分且必要D.既不充分也不必要
3.(5分)已知a,b为非零实数,且a>b,则下列不等式成立的是( )
A.a﹣c>b﹣cB.ac2>bc2C.a2>b2D.
4.(5分)若偶函数f(x)在(﹣∞,﹣1]上是增函数,则下列关系式中成立的是( )
A.B.
C.D.
5.(5分)若,,,则a,b,c的大小关系是( )
A.a>b>cB.b>a>cC.b>c>aD.c>b>a
6.(5分)已知关于x的不等式kx2﹣6kx+k+8>0对任意x∈R恒成立,则k的取值范围是( )
A.0≤k≤1B.0≤k<1C.k<0或k>1D.k≤0或k>1
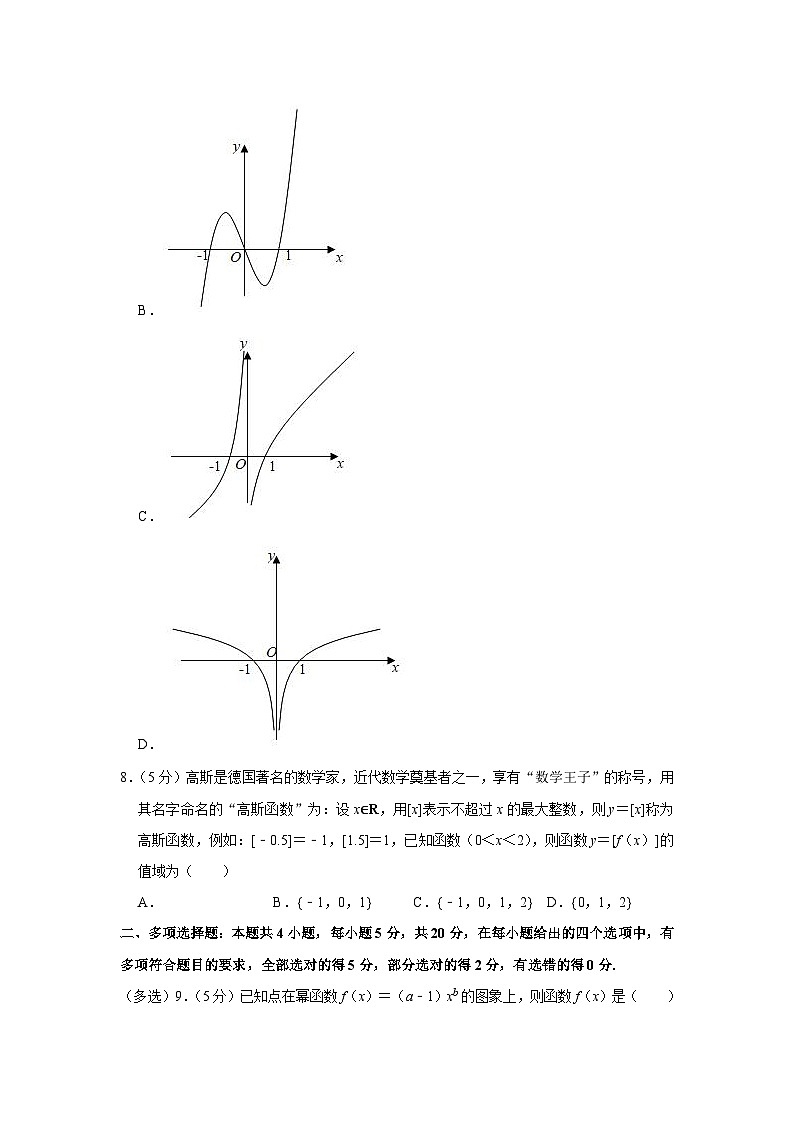
7.(5分)函数f(x)的图象大致为( )
A.
B.
C.
D.
8.(5分)高斯是德国著名的数学家,近代数学奠基者之一,享有“数学王子”的称号,用其名字命名的“高斯函数”为:设x∈R,用[x]表示不超过x的最大整数,则y=[x]称为高斯函数,例如:[﹣0.5]=﹣1,[1.5]=1,已知函数(0<x<2),则函数y=[f(x)]的值域为( )
A.B.{﹣1,0,1}C.{﹣1,0,1,2}D.{0,1,2}
二、多项选择题:本题共4小题,每小题5分,共20分,在每小题给出的四个选项中,有多项符合题目的要求,全部选对的得5分,部分选对的得2分,有选错的得0分.
(多选)9.(5分)已知点在幂函数f(x)=(a﹣1)xb的图象上,则函数f(x)是( )
A.奇函数B.偶函数
C.(0,+∞)上的增函数D.(0,+∞)上的减函数
(多选)10.(5分)下列选项中p是q的充分不必要条件的是( )
A.p:1<x<2,q:1≤x≤2
B.p:xy>1,q:x>1,y>1
C.,q:x<1
D.p:两直线平行,q:内错角相等
(多选)11.(5分)已知函数,则下列结论中正确的是( )
A.f(﹣2)=4B.若f(m)=9,则m=±3
C.f(x)是偶函数D.f(x)在R上单调递减
(多选)12.(5分)下列选项正确的是( )
A.对的最小值为1
B.若ab<0,则的最大值为﹣2
C.若a>0,b>0,则
D.若正实数x,y满足x+2y=1,则的最小值为8
三、填空题:本题共4小题,每小题5分,共20分.
13.(5分)若命题p:∃x∈R,x2﹣2x≥﹣1,则p的否定为 .
14.(5分) .
15.(5分)若在区间(1,+∞)上是增函数,则实数a的取值范围是 .
16.(5分)已知x>0,y>0且1,若x+y>m2+8m恒成立,则实数m的取值范围是 .
四、解答题:本题共6小题,共70分,解答应写出必要的文字说明、证明过程及验算步骤.
17.(10分)在①A∩B=A,②A∩(∁RB)=A,③A∩B=∅,这三个条件中任选一个,补充到下面的问题中,求解下列问题:
已知集合A={x|a﹣1<x<2a+3},B={x|x2﹣2x﹣8≤0}.
(1)当a=2时,求A∪B;
(2)若_____,求实数a的取值范围.
18.(12分)(1)已知x>3,求的最小值,并求取到最小值时x的值;
(2)已知0<x<1,求x(4﹣3x)的最大值.
19.(12分)已知关于x的不等式ax2+(a﹣1)x﹣1>0.
(1)若此不等式的解集为,求实数a的值;
(2)若a∈R,解这个关于x的不等式;
20.(12分)已知函数y=f(x)(x∈R)是偶函数.当x≥0时,f(x)=x2﹣2x.
(1)求函数f(x)的解析式;
(2)若函数f(x)在区间[a,a+2]上单调,求实数a的取值范围;
(3)当a>﹣1时,记f(x)在区间[a,a+2]上的最小值为g(a),求g(a)的表达式.
21.(12分)“绿水青山就是金山银山”,为了保护环境,某工厂在政府部门的鼓励下进行技术改进,把二氧化碳化为某种化工产品,经测算,该处理成本y(单位:万元)与处理量x(单位:吨)之间的函数关系可近似表示为y=x2﹣40x+1600,30≤x≤50,已知每处理一吨二氧化碳可获得价值20万元的某种化工产品.
(1)当处理量为多少吨时,每吨的平均处理成本最少?
(2)判断该技术改进能否获利?如果能获利,求出最大利润;如果不能获利,则国家至少需要补贴多少万元该工厂才不会亏损?
22.(12分)已知函数是定义域上的奇函数,且f(﹣1)=﹣2.
(1)求函数f(x)的解析式;
(2)若方程f(x)=m在(0,+∞)上有两个不同的根,求实数m的取值范围;
(3)令,若对都有,求实数t的取值范围.
2022-2023学年江苏省无锡市市北高级中学高一(上)期中数学试卷
参考答案与试题解析
一、单选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合要求的.
1.(5分)已知R是实数集,集合A={x∈Z||x|<2},B={x|2x﹣1≥0},则A∩(∁RB)=( )
A.B.{1}C.{﹣1,0}D.
【解答】解:由题可知:A={﹣1,0,1},
∴,即A∩(∁RB)={﹣1,0}.
故选:C.
2.(5分)已知x≠0,则“”是“x>2022”的( )条件
A.必要不充分B.充分不必要
C.充分且必要D.既不充分也不必要
【解答】解:“”⇔x<0或x,
当x>2022时,成立
故“”是“x>2022”的必要不充分条件,
故选:A.
3.(5分)已知a,b为非零实数,且a>b,则下列不等式成立的是( )
A.a﹣c>b﹣cB.ac2>bc2C.a2>b2D.
【解答】解:a,b为非零实数,且a>b,
对于A:a﹣c>b﹣c,故A正确;
对于B:若c=0,则ac2=bc2,故B错误;
对于CD:令a=1,b=﹣2,显然不成立,故CD错误;
故选:A.
4.(5分)若偶函数f(x)在(﹣∞,﹣1]上是增函数,则下列关系式中成立的是( )
A.B.
C.D.
【解答】解:∵偶函数f(x)在(﹣∞,﹣1]上是增函数,
∴函数f(x)在[1,+∞)上是减函数,
则f(2)<f()<f(1),
即f(2)<f()<f(﹣1),
故选:A.
5.(5分)若,,,则a,b,c的大小关系是( )
A.a>b>cB.b>a>cC.b>c>aD.c>b>a
【解答】解:∵y在R上是减函数,
∴,
又∵,
∴,
即b>c>a,
故选:C.
6.(5分)已知关于x的不等式kx2﹣6kx+k+8>0对任意x∈R恒成立,则k的取值范围是( )
A.0≤k≤1B.0≤k<1C.k<0或k>1D.k≤0或k>1
【解答】解:关于x的不等式kx2﹣6kx+k+8>0对任意x∈R恒成立,
当k=0时,8>0恒成立;
当k<0时,由y=kx2﹣6kx+k+8的开口向下,不等式不恒成立;
当k>0时,只需Δ<0,即(﹣6k)2﹣4k(k+8)<0,解得0<k<1.
所以k的取值范围是[0,1).
故选:B.
7.(5分)函数f(x)的图象大致为( )
A.
B.
C.
D.
【解答】解:f(﹣x)f(x),则f(x)为偶函数,图象关于y轴对称,排除B,C,
当x>0时,f(x)x为增函数,排除A,
故选:D.
8.(5分)高斯是德国著名的数学家,近代数学奠基者之一,享有“数学王子”的称号,用其名字命名的“高斯函数”为:设x∈R,用[x]表示不超过x的最大整数,则y=[x]称为高斯函数,例如:[﹣0.5]=﹣1,[1.5]=1,已知函数(0<x<2),则函数y=[f(x)]的值域为( )
A.B.{﹣1,0,1}C.{﹣1,0,1,2}D.{0,1,2}
【解答】解:令t=2x∈(1,4),则,
由二次函数的图象及性质可知,当t∈(1,4)时,,
∴[f(t)]∈{﹣1,0,1}.
故选:B.
二、多项选择题:本题共4小题,每小题5分,共20分,在每小题给出的四个选项中,有多项符合题目的要求,全部选对的得5分,部分选对的得2分,有选错的得0分.
(多选)9.(5分)已知点在幂函数f(x)=(a﹣1)xb的图象上,则函数f(x)是( )
A.奇函数B.偶函数
C.(0,+∞)上的增函数D.(0,+∞)上的减函数
【解答】解:由函数f(x)=(a﹣1)xb为幂函数可知,a﹣1=1,则a=2,所以点为,
代入f(x)=xb得,,所以b=﹣1,即.
故函数f(x)为奇函数,且在(0,+∞)上递减.
故选:AD.
(多选)10.(5分)下列选项中p是q的充分不必要条件的是( )
A.p:1<x<2,q:1≤x≤2
B.p:xy>1,q:x>1,y>1
C.,q:x<1
D.p:两直线平行,q:内错角相等
【解答】解:对于A,集合(1,2)是集合[1,2]的真子集,所以p是q的充分不必要条件,A正确;
对于B,当x,y=4时,xy,故由p不能推出q,
反之,由x>1,y>1必定可得到xy>1,所以p是q的必要不充分条件,B不正确.
对于C,由,可得0<x<1,集合(0,1)是集合(﹣∞,1)的真子集,
所以p是q的充分不必要条件,C正确;
对于D,根据平面几何中两条直线平行的判定定理和性质定理,
可知”两直线平行“是”内错角相等“的充要条件,D不正确.
故选:AC.
(多选)11.(5分)已知函数,则下列结论中正确的是( )
A.f(﹣2)=4B.若f(m)=9,则m=±3
C.f(x)是偶函数D.f(x)在R上单调递减
【解答】解:∵,
∴f(﹣2)=4,故A正确;
若f(m)=9,则m2=9且m≤0,解得m=﹣3,故B错误;
作出f(x)的图象如下:
由图可知,f(x)的图象不关于y轴对称,不是偶函数,且在R上单调递减,故C错误,D正确;
故选:AD.
(多选)12.(5分)下列选项正确的是( )
A.对的最小值为1
B.若ab<0,则的最大值为﹣2
C.若a>0,b>0,则
D.若正实数x,y满足x+2y=1,则的最小值为8
【解答】解:对于A,若x<﹣1,则x+1<0,所以x0,所以x的最小值不是1,故A错误,
对于B,∵ab<0,∴0,0,
∴[()+()]2,当且仅当,即a=﹣b时,等号成立,故B正确,
对于C,∵a>0,b>0,∴,当且仅当a=b时,等号成立,故C错误,
对于D,∵x>0,y>0,且x+2y=1,
∴(x+2y)()=44+28,当且仅当,即x,y时,等号成立,
∴的最小值为8,故D正确,
故选:BD.
三、填空题:本题共4小题,每小题5分,共20分.
13.(5分)若命题p:∃x∈R,x2﹣2x≥﹣1,则p的否定为 ∀x∈R,x2﹣2x<﹣1 .
【解答】解:因为特称命题的否定是全称命题,所以:命题p:∃x∈R,x2﹣2x≥﹣1,则p的否定为:∀x∈R,x2﹣2x<﹣1.
故答案为:∀x∈R,x2﹣2x<﹣1.
14.(5分) 18 .
【解答】解:.
故答案为:18.
15.(5分)若在区间(1,+∞)上是增函数,则实数a的取值范围是 (﹣∞,﹣1) .
【解答】解:f(x)a,
∵在区间(1,+∞)上是增函数,
∴a+1<0,
∴a<﹣1,
即实数a的取值范围是(﹣∞,﹣1).
故答案为:(﹣∞,﹣1).
16.(5分)已知x>0,y>0且1,若x+y>m2+8m恒成立,则实数m的取值范围是 (﹣9,1) .
【解答】解:因为x>0,y>0,且1,
所以x+y=(x+y)()=59,当且仅当y=2x时取等号,
要使x+y>m2+8m恒成立,即9>m2+8m恒成立,
解得﹣9<m<1,
即实数m的取值范围是(﹣9,1),
故答案为:(﹣9,1).
四、解答题:本题共6小题,共70分,解答应写出必要的文字说明、证明过程及验算步骤.
17.(10分)在①A∩B=A,②A∩(∁RB)=A,③A∩B=∅,这三个条件中任选一个,补充到下面的问题中,求解下列问题:
已知集合A={x|a﹣1<x<2a+3},B={x|x2﹣2x﹣8≤0}.
(1)当a=2时,求A∪B;
(2)若_____,求实数a的取值范围.
【解答】解:(1)当a=2时,集合A={x|1<x<7},集合B={x|﹣2≤x≤4},
所以A∪B={x|﹣2≤x<7};
(2)选择①:则A⊆B,当A=∅时,a﹣1≥2a+3,解得a≤﹣4,
当A≠∅时,只需,解得﹣1,
综上可得实数a的取值范围为(﹣∞,﹣4]∪.
选择②:A∩(∁RB)=A,则A∩B=∅,
所以当A=∅时,a﹣1≥2a+3,解得a≤﹣4,
当A≠∅时,a﹣1<2a+3,则a>﹣4,
要使A∩B=∅,只需a﹣1≥4或2a+3≤﹣3,解得a≥5或﹣4<a≤﹣3,
综上可得实数a的取值范围为[5,+∞)∪(﹣∞,﹣3].
选择③:解题过程同选择②相同.
18.(12分)(1)已知x>3,求的最小值,并求取到最小值时x的值;
(2)已知0<x<1,求x(4﹣3x)的最大值.
【解答】解:(1)因为x>3,所以x﹣3>0,
故:,
当且仅当即x=5时等号成立,
故当x=5时,y的最小值为7.
(2)因为0<x<1,故4﹣3x>0,
所以,
当且仅当3x=4﹣3x即时取等号,此时x(4﹣3x)取得最大值.
19.(12分)已知关于x的不等式ax2+(a﹣1)x﹣1>0.
(1)若此不等式的解集为,求实数a的值;
(2)若a∈R,解这个关于x的不等式;
【解答】解:(1)不等式ax2+(a﹣1)x﹣1>0可化为(ax﹣1)(x+1)>0,
因为不等式的解集为,
可得﹣1,为方程(ax﹣1)(x+1)=0(a<0)的两根,
可得,解得:a=﹣2.
(2)当a=0时,原不等式即为x+1<0,解得x<﹣1,解集为{x|x<﹣1};
当a>0时,原不等式化为,解集为;
当a<0时,原不等式化为,
①若a=﹣1,可得(x+1)2<0,解集为∅;
②若a<﹣1,,可得解集为;
③若﹣1<a<0,,可得解集为.
故:a=0时,解集为{x|x<﹣1};
a>0时,解集为;
a=﹣1时,解集为∅;
a<﹣1时,解集为;
﹣1<a<0时,解集为.
20.(12分)已知函数y=f(x)(x∈R)是偶函数.当x≥0时,f(x)=x2﹣2x.
(1)求函数f(x)的解析式;
(2)若函数f(x)在区间[a,a+2]上单调,求实数a的取值范围;
(3)当a>﹣1时,记f(x)在区间[a,a+2]上的最小值为g(a),求g(a)的表达式.
【解答】解:(1)设x<0,则﹣x>0,
因为x≥0时,f(x)=x2﹣2x,且f(x)为偶函数,
所以f(﹣x)=(﹣x)2﹣2(﹣x)=x2+2x=f(x),
所以f(x);
(2)由(1)可得其图象如图所示,
因为f(x)在区间[a,a+2]上单调,
由图象可知,a+2≤﹣1或a≥1,
所以a的取值范围(﹣∞,﹣3]∪[1,+∞);
(3)当﹣1<a≤1时,1<a+2≤3,此时g(a)=f(x)min=f(1)=12﹣2×1=﹣1,
当a>1时,f(x)在区间[a,a+2]上单调递增,此时g(a)=f(x)min=f(a)=a2﹣2a,
所以g(a).
21.(12分)“绿水青山就是金山银山”,为了保护环境,某工厂在政府部门的鼓励下进行技术改进,把二氧化碳化为某种化工产品,经测算,该处理成本y(单位:万元)与处理量x(单位:吨)之间的函数关系可近似表示为y=x2﹣40x+1600,30≤x≤50,已知每处理一吨二氧化碳可获得价值20万元的某种化工产品.
(1)当处理量为多少吨时,每吨的平均处理成本最少?
(2)判断该技术改进能否获利?如果能获利,求出最大利润;如果不能获利,则国家至少需要补贴多少万元该工厂才不会亏损?
【解答】解:(1)由题意可得,二氧化碳的平均处理成本P(x),30≤x≤50,
当30≤x≤50时,P(x) ,
当且仅当,即x=40等号成立,
故P(x)取得最小值为P(40)=40,
故当处理量为40吨时,每吨的平均处理成本最少.
(2)当30≤x≤50时,
该工厂获利S,
则S=20x﹣(x2﹣40x+1600)=﹣(x﹣30)2﹣700,
当30≤x≤50时,Smax=﹣700<0,
故该工厂不会获利,国家至少需要补贴700万元,该工厂不会亏损.
22.(12分)已知函数是定义域上的奇函数,且f(﹣1)=﹣2.
(1)求函数f(x)的解析式;
(2)若方程f(x)=m在(0,+∞)上有两个不同的根,求实数m的取值范围;
(3)令,若对都有,求实数t的取值范围.
【解答】解:(1)∵f(﹣1)=﹣2,又f(x)是奇函数,
∴f(1)=2,即,解得,
∴,
经验证,函数满足定义域{x|x≠0},成立,
∴;
(2)方程f(x)=m在(0,+∞)上有两个不同的根,
即x2﹣mx+1=0在(0,+∞)上有两个不相等的实数根,
需满足,解得m>2.
∴实数m的取值范围为(2,+∞);
(3)有题意知,
令,
因为函数在上单调递减,在[1,2]上单调递增,
∴,
∵函数y=z2﹣2tz﹣2的对称轴为z=t<0,
∴函数y=z2﹣2tz﹣2在上单调递增.
当z=2时,ymin=﹣4t+2;当时,;
即h(x)min=﹣4t+2,,
又∵对都有恒成立,
∴,
即,
解得,又∵t<0,
∴t的取值范围是[,0).
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布日期:2023/10/31 9:16:03;用户:高中数学朱老师;邮箱:rFmNt90mRiXzEYJeDrg1uSD0fc@;学号:37103942
相关试卷
这是一份2022-2023学年江苏省无锡市惠山区锡东高级中学高一(下)期中数学试卷(含解析),共23页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
这是一份2020-2021学年江苏省无锡市锡山高级中学高二(上)期中数学试卷,共25页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
这是一份2021-2022学年江苏省无锡市市北高级中学高一(上)期中数学试卷,共14页。试卷主要包含了单选题,多选题,填空题,综合题等内容,欢迎下载使用。









