

初中数学冀教版七年级上册第五章 一元一次方程5.1一元一次方程精品测试题
展开1.下列方程中,是一元一次方程的是( )
A.B.C.D.
2.下列说法中正确的是( )
A.是方程的解B.是方程的解
C.是方程的解D.是方程的解
3.下列运用等式的性质,变形不正确的是( )
A.若,则B.若,则
C.若,则D.若,则
4.在目前的疫情环境下,口罩成了人们生活中的必需品,现某口罩厂共有30名员工,每名员工每天可以生产150个罩面或600个耳绳.已知一个罩面需要配两个耳绳,为使每天生产的罩面和耳绳刚好配套,设安排名员工生产耳绳,则下面所列方程正确的是( )
A.B.
C.D.
5.方程和有相同的解,则的值为( )
A.0B.1C.D.
6.如图,按此规律,第6行最后一个数字是16,第( )行最后一个数是2020.
A.673B.674C.1008D.1010
7.方程 的解为( )
A.B.C.D.
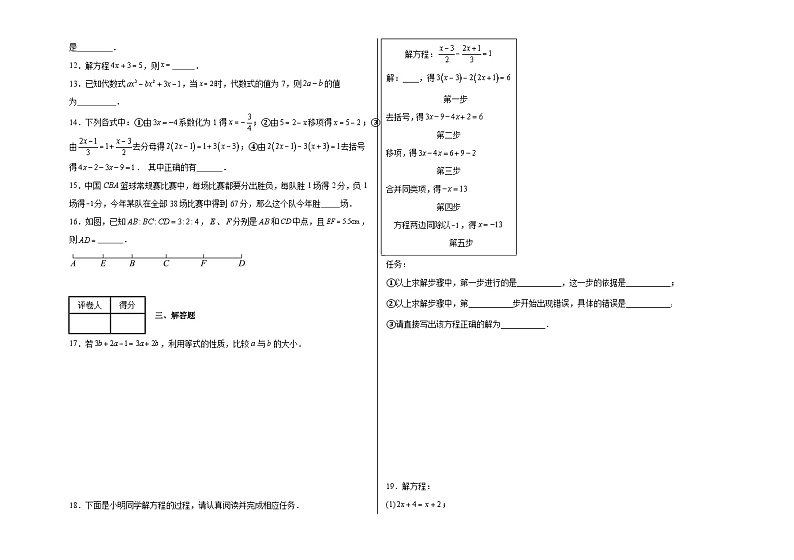
8.已知关于的一元一次方程的解为偶数,则整数的值不可能是( )
A.4B.2C.1D.0
9.习题:甲地到乙地全程是3.3km,一段上坡、一段平路、一段下坡.如果保持上坡每小时走3km,平路每小时走4km,下坡每小时走5km,那么从甲地到乙地需51min,从乙地到甲地需53min.从甲地到乙地时,上坡、平路、下坡的路程各是多少?小红将这个实际问题转化为二元一次方程组问题,设未知数,,已经列出一个方程,则另一个方程正确的是( )
A.B.
C.D.
10.在数轴上,点A对应的数为a,点B对应的数为b,且a,b满足.点P为直线上点B右边的一点,且,点Q为中点,则线段的长为( )
A.6B.8C.10D.15
11.已知关于x的方程(m+3)x|m+4|+18=0是一元一次方程,则m的值是 .
12.解方程,则 .
13.已知代数式,当时,代数式的值为7,则的值为 .
14.下列各式中:①由系数化为1得;②由移项得;③由去分母得;④由去括号得. 其中正确的有 .
15.中国CBA篮球常规赛比赛中,每场比赛都要分出胜负,每队胜1场得2分,负1场得分,今年某队在全部38场比赛中得到67分,那么这个队今年胜 场.
16.如图,已知,、分别是和中点,且,则 .
17.若,利用等式的性质,比较a与b的大小.
18.下面是小明同学解方程的过程,请认真阅读并完成相应任务.
任务:
①以上求解步骤中,第一步进行的是___________,这一步的依据是___________;
②以上求解步骤中,第___________步开始出现错误,具体的错误是___________﹔
③请直接写出该方程正确的解为___________.
19.解方程:
(1);
(2).
20.计算:.圆圆在做作业时,发现题中有一个数字被墨水污染了.
(1)如果被污染的数字是,请计算.
(2)如果计算结果等于6,求被污染的数字.
21.定义一种新运算“”,其运算方式如下:
,
,
,
,
.
观察式子的运算方式,请解决下列问题:
(1)这种运算方式是:______;用含,的式子表示
(2)试比较与的大小;
(3)若关于的方程的解为正整数,求整数的值.
22.已知数轴上两点,表示的数分别为,.
(1)动点从出发,以每秒3个单位的速度沿数轴向右匀速运动.另一动点 从出发,以每秒1个单位的速度沿数轴向右匀速运动,若点、同时出发,点运动 秒追上点,此时点在数轴上表示的数是 .
(2)若点从出发,以每秒2个单位的速度沿数轴向右匀速运动,点从出发,以每秒1个单位的速度沿数轴向左匀速运动,设点、同时出发,运动时间为 秒,试探究:为何值时,点、两点间的距离为4个单位?
23.列方程解应用题:
一商场经销的、两种商品,种商品每件进价40元,利润率为;种商品每件进价50元,售价80元.
(1)种商品每件售价为 元,每件种商品利润率为 .
(2)若该商场同时购进、两种商品共50件,恰好总进价为2100元,求购进种商品多少件?
(3)在“春节”期间,该商场只对、两种商品进行如下的优惠促销活动:
按上述优惠条件,若小华一次性购买、商品实际付款522元,求若没有优惠促销,小华在该商场购买同样商品要付多少元?
评卷人
得分
一、单选题
评卷人
得分
二、填空题
评卷人
得分
三、解答题
解方程:
解:____,得 第一步
去括号,得 第二步
移项,得 第三步
合并同类项,得 第四步
方程两边同除以,得 第五步
打折前一次性购物总金额
优惠措施
少于等于450元
不优惠
超过450元,但不超过600元
按总售价打九折
超过600元
其中600元部分八折优惠,超过600元的部分打七折优惠
参考答案:
1.A
【分析】根据一元一次方程的定义,含有1个未知数,且未知数的次数是1的整式方程,据此即可判断.
【详解】选项A、该方程是一元一次方程,故本选项符合题意;
选项B、该方程中含有2个未知数,不是一元一次方程,故本选项不符合题意;
选项C、该方程未知数项的最高次数是2,不是一元一次方程,故本选项不符合题意;
选项D、该方程不是整式方程,故本选项不符合题意.
故选:A.
【点睛】本题考查了一元一次方程的定义,能熟记一元一次方程的定义的内容是解此题的关键.
2.C
【分析】将解代入到方程中,根据等式是否成立,逐一进行判断即可.
【详解】解:A、当时,,选项错误,不符合题意;
B、当时,,选项错误,不符合题意;
C、当时,,选项正确,符合题意;
D、当时,,选项错误,不符合题意;
故选C.
【点睛】本题考查一元一次方程的解的定义.熟练掌握方程的解,是使等式成立的未知数的值,是解题的关键.
3.D
【分析】直接利用等式的基本性质进而判断得出即可.
【详解】解:A、若,则,正确,不合题意;
B、若,则,正确,不合题意;
C、若,则,正确,不合题意;
D、若,,则,故此选项错误,符合题意;
故选:D.
【点睛】此题主要考查了等式的性质,解题的关键是熟练掌握等式的性质,注意等式的性质2中是除以同一个不为0的数或式子,等式不变.等式的性质:①等式两边加同一个数(或整式)结果仍得等式;②等式两边乘同一个数或除以一个不为零的数,结果仍得等式.
4.D
【分析】根据题意,找出等量关系即可列出方程.生产的罩面数量×2=生产的耳绳数量.
【详解】解:设安排名员工生产耳绳,则安排名员工生产罩面,
根据题意可列方程∶ .
故选:D.
【点睛】本题主要考查了一元一次方程的实际应用,解题的关键是正确理解题意,根据题意找出等量关系列出方程.
5.D
【分析】解得,把代入,即可求解.
【详解】解:,
∴,
∵方程和有相同的解,
∴把代入得,,
∴,
故选:.
【点睛】本题主要考查的解一元一次方程,掌握移项、合并同类项、系数化为解一元一次方程是解题的关键.
6.B
【分析】每一行的最后一个数字分别是1,4,7,10…,易得第n行的最后一个数字为,由此建立方程求得最后一个数是2020在哪一行.
【详解】解:∵每一行的最后一个数分别是1,4,7,10…,
∴第n行的最后一个数字为,
∴,
解得.
因此第674行最后一个数是2020.
故选:B.
【点睛】本题考查数字的变化规律,根据数字的排列规律,找出数字之间的联系,得出运算规律解决问题.
7.B
【分析】方程去分母,去括号,移项,合并同类项,化系数为1,即可求解.
【详解】解:
故选:B.
【点睛】本题考查了解一元一次方程,掌握一元一次方程的解法是解本题的关键.
8.C
【分析】由得,,解得,,的值是偶数,满足条件的值分别是,,,,由此即可求解.
【详解】解:由得,,解得,,
∵的值是偶数,
的值可能为、、、时,的值分别是,,,,符合题意,
∴的值可能为,,、,
∴整数的值不可能是.
故选:.
【点睛】本题主要考查一元一次方程中未知数的取值情况,掌握一元一次方程中未知数的取值不同求参数是解题的关键.
9.C
【分析】根据小红列出的方程可知,小红设从甲地到乙地上坡为xkm,平路为ykm,下坡为km,因此从乙地到甲地上坡为km,平路为ykm,则下坡为xkm,根据从乙地到甲地需53min,列出方程即可.
【详解】解:∵小红列的方程为,
∴小红是设从甲地到乙地上坡为xkm,平路为ykm,下坡为km,
∴从乙地到甲地上坡为km,平路为ykm,则下坡为xkm,
∵从乙地到甲地需53min,
∴可以列方程为:,故C正确.
故选:C.
【点睛】本题主要考查了一元一次方程的应用,根据题意得出x、y表示的意义,找出等量关系,是解题的关键.
10.C
【分析】根据a、b满足,即可得到a、b的值,从而可以得到点A,B所表示的数;设点P表示的数为m,先根据中点的定义表示点Q,根据数轴上两点的距离表示,列方程可得结论.
【详解】解:∵,
∴,
解得,
即点A,B所表示的数分别为,3;
设点P表示的数为m,
∵点P在直线上点B右边一点,
∴,
∵点Q为的中点,
∴
∴点Q表示的数为:
∵,
∴,
∴,
∴.
故选:C.
【点睛】本题考查一元一次方程的应用、非负数的性质、数轴,解答本题的关键是明确题意,利用数轴上两点的距离表示线段的长.
11.
【分析】根据一元一次方程的概念,可得且,求解即可.
【详解】解:由题意可得且,
由可得,
由可得或
综上:
故答案为:
【点睛】此题考查了一元一次方程的概念,解题的关键是掌握一元一次方程的概念,只含有一个未知数且未知数最高次数为1的整式方程.
12./
【分析】根据解一元一次方程的基本步骤“去括号,移项,合并同类项,系数化为”逐个求解即可.
【详解】解:,
移项,得,
合并同类项,得,
系数化为,得,
故答案为:
【点睛】本题考查了解一元一次方程,熟练掌握解一元一次方程的基本步骤是解决本题的关键.
13.
【分析】把代入代数式可得,再变形即可得到答案.
【详解】解:∵代数式,当时,代数式的值为7,
∴,
∴,
∴,
故答案为:.
【点睛】本题考查的是求解代数式的值,等式的基本性质,掌握“整体法求解代数式的值”是解本题的关键.
14.④
【分析】根据解一元一次方程的各步骤的运算要求来判断各式是否正确,即可获解.
【详解】解:①由系数化为1得,故①错误,不符合题意;
②由移项得,故②错误,不符合题意;
③由去分母得,故③错误,不符合题意;
④由去括号得,故④正确,符合题意;
其中正确的有:④;
故答案为:④.
【点睛】此题考查了一元一次方程中的解法,熟练掌握解一元一次方程的去分母、去括号、移项、系数化为1等各个步骤,是解答此题的关键.
15.35
【分析】设胜了x场,那么负了场,根据“在全部38场比赛中得到67分”可列方程并求解.
【详解】解:设胜了x场,由题意得:
,
解得.
答:这个队今年胜了35场.
故答案为:35.
【点睛】本题考查了一元一次方程的应用.解决问题的关键是读懂题意,找到关键描述语,找到所求的量的等量关系.
16./9厘米
【分析】,然后分别求出,,再由得到,解方程即可得到答案.
【详解】解:设.
∵,
∴,
∴,
∵、分别是和中点,
∴,;
又∵,,
∴,
解得,,
∴.
故答案为:.
【点睛】本题主要考查了与线段中点有关的线段和差计算,一元一次方程的应用,正确得到,是解题的关键.
17.
【分析】利用等式的性质将一个字母用另一个字母表示出来,再判断即可.
【详解】解:等式两边同减去,得: ,
等式两边同减去,得: ,
等式两边再同时加上1,得:,
∵,
∴.
【点睛】本题主要考查了等式的基本性质.等式性质1:等式的两边同时加上或减去同一个数或字母,等式仍成立;等式性质2:等式的两边同时乘以或除以同一个不为0数或字母,等式仍成立,熟练运用等式的性质进行变形是解决本题的关键.
18.去分母,等式的性质2,二, 去括号时没有变号,
【分析】先去分母,再去括号,再移项,合并同类项,最后把未知数的系数化1,即可得到答案.
【详解】解:解方程:
①去分母,得 ,(依据是:等式的性质2)
②去括号,得 ,(原解法出现错误,去括号,没有改变符号)
移项,得 ,
合并同类项,得 ,
③方程两边同除以,得.
【点睛】本题考查的是一元一次方程的解法,掌握“解一元一次方程的步骤”是解本题的关键.
19.(1);
(2).
【分析】(1)先移项、再合并同类项即可;
(2)先去分母,再去括号、移项、合并同类项、把x的系数化为1.
【详解】(1)解:,
移项得,,
合并同类项得,;
(2)解:,
去分母得,,
去括号得,,
移项得,,
合并同类项得,,
x的系数化为1得,.
【点睛】本题考查的是解一元一次方程,熟知解一元一次方程的一般步骤是解题的关键.
20.(1)-9
(2)3
【分析】(1)根据有理数混合运算法则计算即可;
(2)设被污染的数字为x,由题意,得,解方程即可;
【详解】(1)解:;
(2)设被污染的数字为x,
由题意,得,解得,
所以被污染的数字是3.
【点睛】本题主要考查有理数的混合运算、一元一次方程的应用,掌握相关运算法则和步骤是接替的关键.
21.(1);
(2);
(3)1或3.
【分析】(1)根据题意给出的算法规律即可求出答案.
(2)根据新定义运算法则进行化简,然后作差比较大小即可求出答案.
(3)由题意将化简,再根据解为正整数,为整数即可求出答案.
【详解】(1)解:由题意给出的规律可知:
(2)解:
,
.
(3)解:
,
,
,
是正整数,是整数,
或
【点睛】本题考查新定义运算和整式的运算,解题的关键是正确理解新定义运算法则.
22.(1),
(2)秒或秒
【分析】(1)用含的代数式表示,运动后表示的数,列方程可得答案;
( 2)用含的代数式表示,运动后表示的数,列方程可得答案.
【详解】(1)解:设点、运动时间是秒,则运动后表示的数是,运动后表示的数是,
根据题意得:,
解得,
∴点运动秒追上点,此时点在数轴上表示的数是,
故答案为:3,5;
(2)当点、运动时间为秒时,点在数轴上表示的数是,点R在数轴上表示的数是,
根据题意得:,
化简得:或,
解得或,
答:当秒或秒时,点、两点间的距离为4个单位.
【点睛】本题考查一元一次方程的应用,解题的关键是能用含的代数式表示点运动后表示的数.
23.(1)60;60;
(2)购进种商品40件;
(3)小华在该商场购买同样商品要付580元或660元
【分析】(1)根据利润等于进价乘以利润率,利润等于售价减进价,列式计算即可;
(2)设购进甲种商品件,则购进乙种商品件,根据总进价为2100元,列出方程,进行求解即可;
(3)设小华打折前应付款为元,分①打折前购物金额超过450元,但不超过600元,②打折前购物金额超过600元,两种情况,分别列方程进行求解即可.
【详解】(1)设种商品每件售价为元,
则,
解得:.
故种商品每件售价为60元;
每件种商品利润率为.
故答案为:60;60;
(2)设购进种商品件,则购进种商品件,
由题意得,
解得:.
故购进种商品40件;
(3)设小华打折前应付款为元,
①打折前购物金额超过450元,但不超过600元,
由题意得,
解得:;
②打折前购物金额超过600元,
,
解得:.
综上可得,小华在该商场购买同样商品要付580元或660元.
【点睛】本题考查一元一次方程的应用.熟练掌握:利润等于进价乘以利润率,利润等于售价减进价,折扣价等于原售价乘以折扣率,是解题的关键.注意分类讨论.
冀教版数学七年级上册第五章一元一次方程章节提升练习: 这是一份冀教版数学七年级上册第五章一元一次方程章节提升练习,共6页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
冀教版数学七年级上册第五章一元一次方程章节基础练习: 这是一份冀教版数学七年级上册第五章一元一次方程章节基础练习,共6页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
冀教版数学七年级上册第五章一元一次方程章节拔高练习: 这是一份冀教版数学七年级上册第五章一元一次方程章节拔高练习,共6页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。













