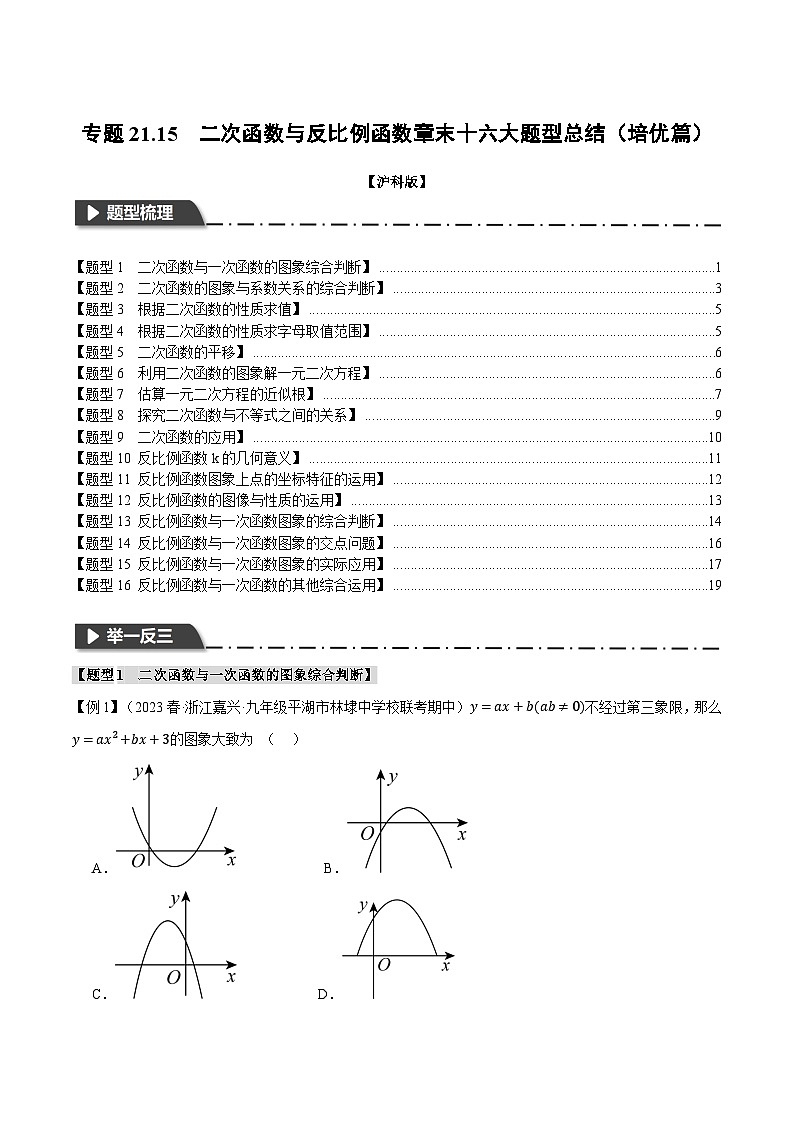
初中数学沪科版九年级上册21.5 反比例函数优秀一课一练

这是一份初中数学沪科版九年级上册21.5 反比例函数优秀一课一练，文件包含专题228相似形章末拔尖卷沪科版原卷版docx、专题228相似形章末拔尖卷沪科版解析版docx等2份试卷配套教学资源，其中试卷共41页， 欢迎下载使用。


TOC \ "1-3" \h \u
\l "_Tc18842" 【题型1 二次函数与一次函数的图象综合判断】 PAGEREF _Tc18842 \h 1
\l "_Tc31647" 【题型2 二次函数的图象与系数关系的综合判断】 PAGEREF _Tc31647 \h 3
\l "_Tc31856" 【题型3 根据二次函数的性质求值】 PAGEREF _Tc31856 \h 5
\l "_Tc31055" 【题型4 根据二次函数的性质求字母取值范围】 PAGEREF _Tc31055 \h 5
\l "_Tc30964" 【题型5 二次函数的平移】 PAGEREF _Tc30964 \h 6
\l "_Tc31406" 【题型6 利用二次函数的图象解一元二次方程】 PAGEREF _Tc31406 \h 6
\l "_Tc2353" 【题型7 估算一元二次方程的近似根】 PAGEREF _Tc2353 \h 7
\l "_Tc8577" 【题型8 探究二次函数与不等式之间的关系】 PAGEREF _Tc8577 \h 9
\l "_Tc20538" 【题型9 二次函数的应用】 PAGEREF _Tc20538 \h 10
\l "_Tc21376" 【题型10 反比例函数k的几何意义】 PAGEREF _Tc21376 \h 11
\l "_Tc30735" 【题型11 反比例函数图象上点的坐标特征的运用】 PAGEREF _Tc30735 \h 12
\l "_Tc10541" 【题型12 反比例函数的图像与性质的运用】 PAGEREF _Tc10541 \h 13
\l "_Tc31649" 【题型13 反比例函数与一次函数图象的综合判断】 PAGEREF _Tc31649 \h 14
\l "_Tc19527" 【题型14 反比例函数与一次函数图象的交点问题】 PAGEREF _Tc19527 \h 16
\l "_Tc22018" 【题型15 反比例函数与一次函数图象的实际应用】 PAGEREF _Tc22018 \h 17
\l "_Tc2746" 【题型16 反比例函数与一次函数的其他综合运用】 PAGEREF _Tc2746 \h 19
【题型1 二次函数与一次函数的图象综合判断】
【例1】（2023春·浙江嘉兴·九年级平湖市林埭中学校联考期中）y=ax+b(ab≠0)不经过第三象限，那么y=ax2+bx+3的图象大致为 （ ）
A． B．
C． D．
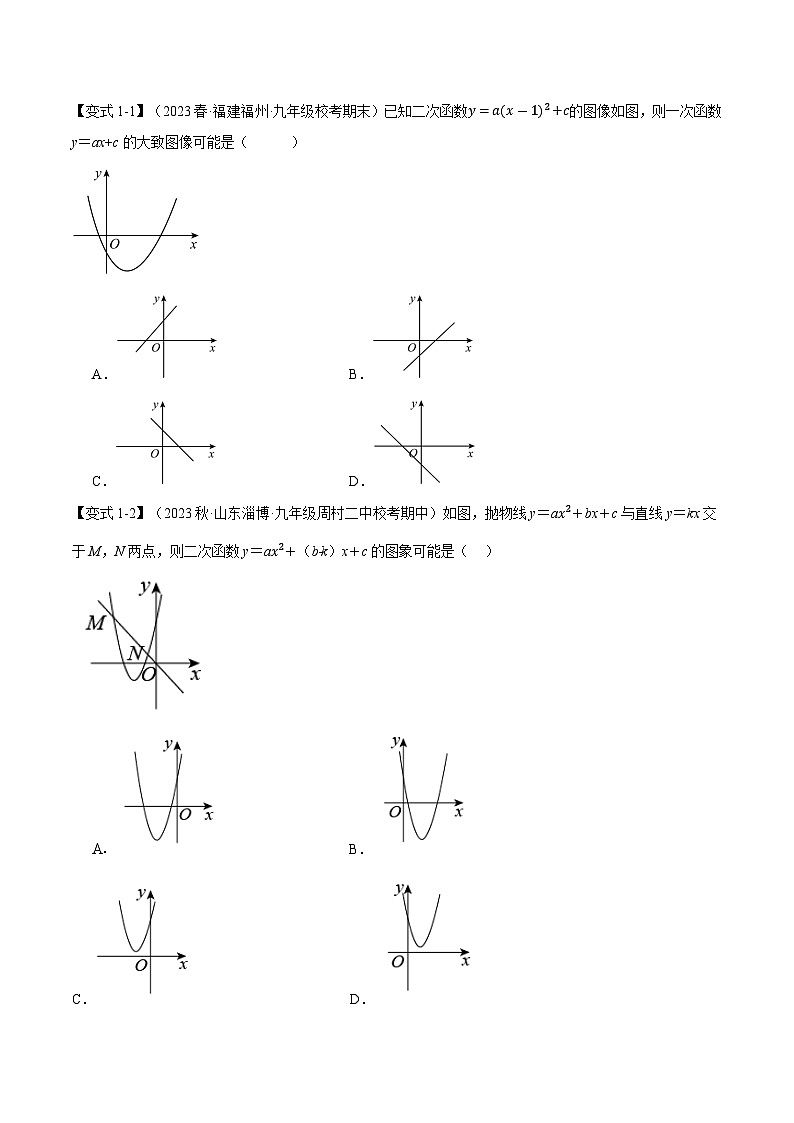
【变式1-1】（2023春·福建福州·九年级校考期末）已知二次函数y=a(x-1)2+c的图像如图，则一次函数y＝ax+c的大致图像可能是（ ）
A．B．
C．D．
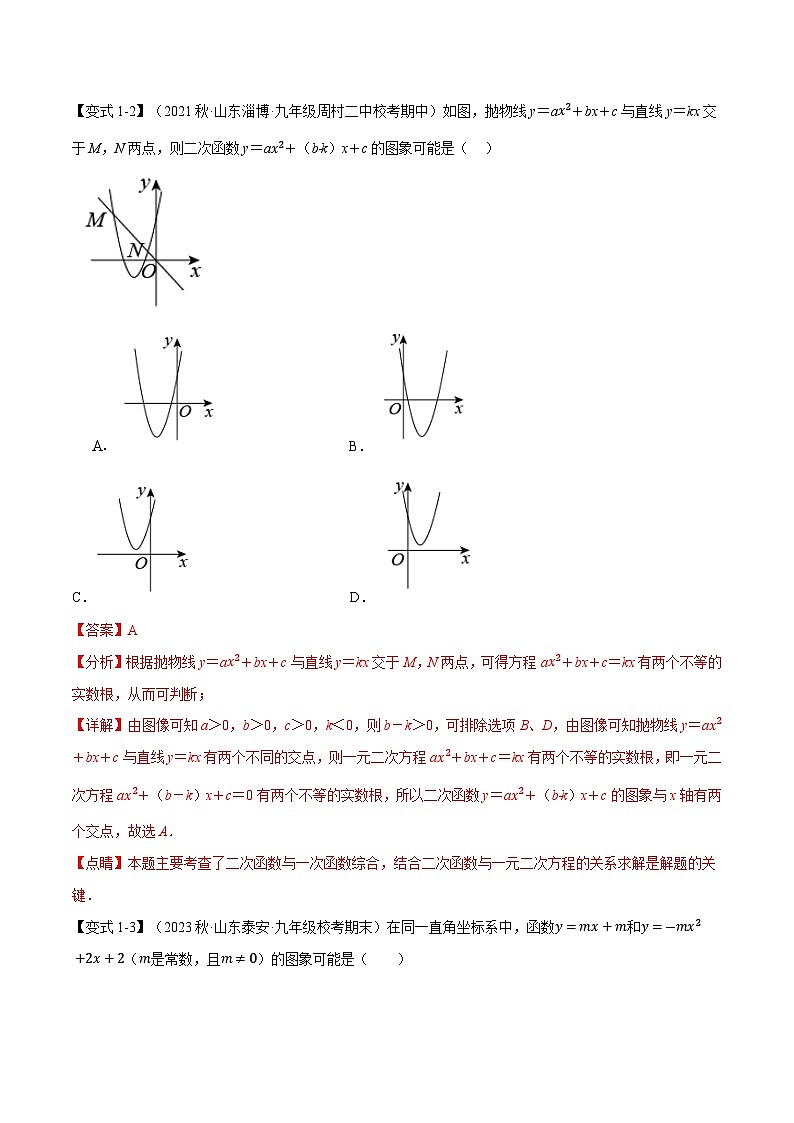
【变式1-2】（2023秋·山东淄博·九年级周村二中校考期中）如图，抛物线y＝ax2＋bx＋c与直线y＝kx交于M，N两点，则二次函数y＝ax2＋（b﹣k）x＋c的图象可能是（ ）
B．
C． D．
【变式1-3】（2023秋·山东泰安·九年级校考期末）在同一直角坐标系中，函数y=mx+m和y=-mx2+2x+2（m是常数，且m≠0）的图象可能是（ ）
A．B．
C．D．
【题型2 二次函数的图象与系数关系的综合判断】
【例2】（2023秋·安徽安庆·九年级安庆市石化第一中学校考期中）如图是二次函数y=ax2+bx+ca≠0图像的一部分，对称轴为x=12，且经过点2,0，下列说法：①abc>0；②a+b=0；③4a+2b+c<0；④若-2020,y1,2022,y2是抛物线上的两点，则y1>y2；⑤14b>mam+b，（其中m≠12）；其中说法正确的是（ ）

A．①②③B．②④⑤C．②③④D．①④⑤
【变式2-1】（2023春·湖南长沙·九年级校联考期末）如图，二次函数y=ax2+bx+c的图像经过点A(-1,0)、点B(3,0)、点C(4,y1)，若点D(x2,y2)是抛物线上任意一点，有下列结论：①abc>0；②4a-2b+c<0；③二次函数y=ax2+bx+c的最小值为-4a；④若y2>y1，则x2>4；⑤一元二次方程bx2+cx-a=0的两个根为-1和-12．其中正确结论的是 (填序号)．
【变式2-2】（2023秋·福建漳州·九年级统考期末）二次函数y=ax2+bx+c（a<0）的图象过点A（m，n），B（-2-m，n），C（-1，4）．现给出以下结论：
①b-2a=0；
②c=a+4；
③对于任意实数p，不等式ap2+bp≤a-b一定成立；
④关于t的方程a（t-1）2+b（t-1）+c-5=0有实数根．
其中正确的是 ．（写出所有正确结论的序号）
【变式2-3】（2023秋·重庆·九年级期末）如图，函数y=ax2+bx+c的图象过点(-1,0)和(m,0)，下列判断：
①abc<0；
②a+4c<2b；
③|m+1|=|b2-4aca|；
④x=2和x=m-3处的函数值相等．
其中正确的是 （只填序号）．
【题型3 根据二次函数的性质求值】
【例3】（2023秋·湖北武汉·九年级校考期中）二次函数y=x2-2x-2022的图象上有两点Aa,-1和Bb,-1，则a2+2b-3的值等于（ ）
A．2020B．2021C．2022D．2023
【变式3-1】（2023秋·广东广州·九年级统考期末）二次函数y=-x2-2x+m，在-3≤x≤2的范围内有最小值-3，则m的值是（ ）
A．-6B．-2C．2D．5
【变式3-2】（2023秋·湖北武汉·九年级校考期中）已知点Pa,b是二次函数y=-x-m2+m2+1图象上一点，当-2≤a≤1时，b的最大值为4，则实数m的值为 ．
【变式3-3】（2023秋·浙江温州·九年级统考期末）已知二次函数y=ax2+4ax+3a-1的图象开口向下.
(1)若点m,-9和1,-9是该图象上不同的两点，求m的值．
(2)当-4≤x≤4时，函数的最大值与最小值的差为6，求a的值．
【题型4 根据二次函数的性质求字母取值范围】
【例4】（2023春·江西九江·九年级校考期中）已知三个不重合的点An,y1,B1-n,y2,C-1,y3均在抛物线y=ax2+bx+ca≠0上，且2an+b=0，点B，C在抛物线对称轴同侧．若y1>y2>y3，则n的取值范围为（ ）
A．n>2B．n<2C．12-32
【变式4-1】（2023秋·浙江杭州·九年级校联考期末）若二次函数y＝ax2+bx+c（a≠0）的图象的顶点在第一象限，且过点（0，1）和（﹣1，0）．则S＝a+b+c的值的变化范围是 ．
【变式4-2】（2023秋·云南德宏·九年级统考期末）二次函数y=ax2+bx+c，自变量x与函数y的对应值如表：
则当-2【变式4-3】（2023秋·浙江丽水·九年级校联考期中）已知二次函数y＝-（x－m）2＋m2＋1，且-2≤x≤32．
（1）当m＝1时，函数y有最大值 ．
（2）当函数值y恒不大于4时，实数m的范围为 ．
【题型5 二次函数的平移】
【例5】（2023秋·甘肃兰州·九年级校考期末）如图，在平面直角坐标系中，二次函数y=-12x2+b的图象经过正方形ABOC的顶点A,B,C，且A点为顶点，将该抛物线经过平移，使其顶点为C点，则平移后抛物线的表达式为（ ）

A．y=-12x-22+2B．y=-12x+22+2
C．y=2x+22-2D．y=2x-22+2
【变式5-1】（2023秋·山东东营·九年级东营市胜利第一初级中学校考期末）将抛物线y=-x2-2x+3的图象向右平移1个单位，再向下平移2个单位得到的抛物线的顶点是（ ）
A．(-1,4)B．(1,-2)C．(0,-2)D．(0,2)
【变式5-2】（2023秋·浙江宁波·九年级统考期末）将抛物线y=x2+3x-6向上平移m个单位后，得到的图象不经过第四象限，则m的值可能是（ ）
A．1B．3C．5D．7
【变式5-3】（2023秋·河北张家口·九年级张家口市实验中学校考期中）在平面直角坐标系中，已知点A(1,3)，B(3,5)，C(3,-7)，直线l:y=x+m经过点A，抛物线L:y=ax2+bx+2恰好经过A，B，C三点中的两点．
(1)判断点B是否在直线l上，并说明理由；
(2)求a,b的值；
(3)平移抛物线L，
①使其顶点为B，求此时抛物线与y轴交点的坐标；
②使其顶点仍在直线l上，求平移后所得抛物线与y轴交点纵坐标的最大值．
【题型6 利用二次函数的图象解一元二次方程】
【例6】（2023秋·河南周口·九年级统考期末）二次函数y=ax2+bx的图象如图所示，若一元二次方程ax2+bx+m=0有实数根，则m的最大值为（ ）

A．-3B．3C．-5D．9
【变式6-1】（2023秋·宁夏石嘴山·九年级校考期中）抛物线图象如图所示，求解一元二次方程．
(1)方程ax2+bx+c＝0的根为 ；
(2)方程ax2+bx+c＝﹣3的根为 ；
(3)方程ax2+bx+c＝﹣4的根为 ；
【变式6-2】（2023秋·浙江台州·九年级统考期末）二次函数y=ax2-bx-5的图象与x轴交于(1,0)、(-3,0)，则关于x的方程ax2-bx=5的解为（ ）
A．1，3B．1，-5 C．-1，3D．1，-3
【变式6-3】（2023秋·浙江丽水·九年级期末）二次函数y=ax2+bx+c的部分对应值列表如下：
则一元二次方程a(2x-1)2+b(2x-1)+c=7的解为 ．
【题型7 估算一元二次方程的近似根】
【例7】（2023秋·广东东莞·九年级东莞市东华初级中学校考期末）根据下面表格中的对应值：
判断方程ax2+bx+c=0(a≠0，a，b，c为常数）的一个解x的范围是（ ）
A．3.22C．3.24【变式7-1】（2023秋·福建厦门·九年级厦门一中校考期中）如图，以直线x=1为对称轴的二次函数y=ax2+bx+c的图象与x轴负半轴交于A点，则一元二次方程ax2+bx+c=0的正数解的范围是（ ）．

A．2【变式7-2】（2023秋·北京丰台·九年级统考期中）在关于的x二次函数中，自变量x可以取任意实数，下表是自变量x与函数y的几组对应值：
根据以上信息，关于x的一元二次方程ax2+bx+c=0的两个实数根中，其中的一个实数根约等于 （结果保留小数点后一位）．
【变式7-3】（2023春·黑龙江绥化·九年级绥化市第八中学校校考期中）二次函数y=2x2+4x-1的图象如图所示，若方程2x2+4x-1=0的一个近似根是x=-2.2，则方程的另一个近似根为 ．（结果精确到0.1）
【题型8 探究二次函数与不等式之间的关系】
【例8】（2023秋·海南省直辖县级单位·九年级统考期末）抛物线y=ax2+bx+c的部分图象如图所示，则当y>0时，x的取值范围是（ ）
A．x>-1B．x<-1C．-13
【变式8-1】（2023秋·北京石景山·九年级校考期中）已知二次函数y=x2+2x-3
(1)用配方法将其化为y=ax-h2+k的形式；
(2)结合函数图象直接写出当y>-3时，x的取值范围．
【变式8-2】（2023秋·安徽滁州·九年级校考阶段练习）已知，在同一坐标系中二次函数y1＝ax2+bx+c与一次函数y2＝mx+n的图象如图，它们相交于点B（0，2），C（3，8），抛物线的顶点D（1，0），直线BC交x轴于点A．
（1）当y1＜y2时，x的取值范围是 ．
（2）当y1y2＞0时，x的取值范围是 ．
【变式8-3】（2023秋·广西南宁·九年级南宁二中校考期中）如图，直线y1=kx+b与抛物线y2=ax2+bx+c交于点A-2,3和点B2,-1，若y2【题型9 二次函数的应用】
【例9】（2023秋·辽宁鞍山·九年级统考期末）某校数学兴趣小组对我市某大型商场的停车场车流量进行了调查，某天上午从开业开始一小时内累计进入商场停车场的车数y（单位：辆）与时间x（单位：分钟）的变化情况，发现其变化规律符合二次函数关系式：y=ax2+bx+c0≤x≤60，数据如表．
(1)求a，b，c的值；
(2)如果平均每辆车载入停车场2名顾客，顾客需下车排队“测体温”，体温正常可以从停车场进入商场，若所有驾车的顾客都体温正常，且平均每分钟有16名顾客经过“测体温”进入商场，求排队人数的最大值．（排队人数＝累计人数－已进入商场人数）
【变式9-1】（2023秋·辽宁盘锦·九年级统考期末）某果园有100棵橙子树，平均每棵树结600个橙子．现准备多种一些橙子树以提高果园产量，但是如果多种树，那么树之间的距离和每一棵树所接受的阳光就会减少．根据经验估计，每多种一棵树，平均每棵树就会少结5个橙子．
(1)假设果园增种x棵橙子树，那么果园共有______棵橙子树；这时平均每棵树结______个橙子．
(2)在（1）的条件下，求增种多少棵橙子树，可以使果园橙子总产量最大？最大产量是多少？
【变式9-2】（2023秋·辽宁盘锦·九年级校考期中）某商店经营儿童益智玩具，已知成批购进时的单价是20元．调查发现：销售单价是30元时，月销售量是230件，而销售单价每上涨1元，月销售量就减少10件，但每件玩具售价不能高于40元． 设每件玩具的销售单价上涨了x元时（x为正整数），月销售利润为y元．
(1)求y与x的函数关系式并直接写出自变量x的取值范围．
(2)每件玩具的售价定为多少元时，月销售利润恰为2520元？
(3)每件玩具的售价定为多少元时可使月销售利润最大？
【变式9-3】（2023秋·江苏泰州·九年级统考期末）自新冠疫情防控“新十条”发布以来，市场上对日常居民所用消毒液的需求量日益加大，某消毒液厂为满足市场需求，改造了10条消毒液生产线，每条生产线每天可生产消毒液300吨．由于人员和资金限制，如果每增加一条生产线，每条生产线每天就会少生产20吨消毒液．设增加x条生产线(x为正整数)，每条生产线每天可生产消毒液y吨
(1)y与x之间的函数关系式为___________；
(2)设该厂每天可以生产消毒液w吨，请求出w与x的函数关系式，并求出当x为多少时，每天生产的消毒液最多？最多为多少吨？
【题型10 反比例函数k的几何意义】
【例10】（2023春·湖南衡阳·九年级校考期中）如下图，过反比例函数y=2x（x>0）图像上的一点A作y轴的平行线交反比例函数y=kx（x>0）于点B，连接OA、OB．若S△AOB=3，则k的值为（ ）

A．4B．-2C．-4D．-1
【变式10-1】（2023春·江苏无锡·九年级统考期末）如图，在平面直角坐标系中有一个6×2的矩形ABCD网格，每个小正方形的边长都是1 个单位长度，反比例函数y=-32xx<0的图像经过格点E（小正方形的顶点），反比例函数y=52xx>0的图像经过格点F，同时还经过矩形ABCD的边CD上的G点，连接EG,FG，则△EFG的面积为 ．

【变式10-2】（2023秋·河南开封·九年级开封市第十三中学校考期末）如图，点A是反比例函数y=mx(x<0)图象上一点，AC⊥x轴于点C，与反比例函数 y=nx(x<0)图象交于点B，AC＝3BC，连接OA，OB，若△OAB的面积为2，则m+n=（ ）
A．-4B．-8C．-10D．-12
【变式10-3】（2023春·黑龙江大庆·九年级校考期末）如图，A、B是函数y=6x上两点，P为一动点，作PB∥y轴，PA∥x轴，下列说法正确的是（ ）
①△AOP≌△BOP；②S△AOP=S△BOP；③若OA=OB，则OP平分∠AOB；④若S△BOP=2，则S△ABP=8

A．①③B．②③C．②④D．③④
【题型11 反比例函数图象上点的坐标特征的运用】
【例11】（2023春·江苏常州·九年级统考期末）已知反比例函数的图象经过三个点（﹣3，﹣4）、（2m，y1）、（6m，y2），其中m＞0，当y1﹣y2＝4时，则m＝ ．
【变式11-1】（2023秋·辽宁沈阳·九年级统考期中）已知反比例函数y=kx(k≠0)，在每一个象限内，y随x的增大而增大，则下列点可能在这个函数图象上的为（ ）
A．(2,3)B．(-2,3)C．(0,3)D．(-2,0)
【变式11-2】（2023秋·广西北海·九年级统考期中）如图，点A是反比例函数图象上一点，则下列各点在该函数图象上的是（ ）
A．(-1,-1)B．(1,-1)C．2,12D．(-2,1)
【变式11-3】（2023秋·黑龙江哈尔滨·九年级校考期中）在平面直角坐标系中，点A-2，3，B3，2，C(-6,m)分别在三个不同的象限，若反比例函数y=kxk≠0的图象经过其中两点则m的值为（ ）
A．1B．-1C．-6D．6
【题型12 反比例函数的图像与性质的运用】
【例12】（2023春·浙江温州·九年级统考期末）已知反比例函数y=kx(k≠0)，当-2≤x≤-1时，y的最大值是4，则当x≥2时，y有（ ）
A．最小值-4B．最小值-2C．最大值-4D．最大值-2
【变式12-1】（2023秋·河南三门峡·九年级统考期末）已知反比例函数y=3x，下列结论中不正确的是（ ）
A．其图象经过点-1,-3B．其图象分别位于第一、第三象限
C．当x>1时，0【变式12-2】（2023秋·河南平顶山·九年级统考期末）点A-3,y1、B-1,y2、C2,y3都在反比例函数y=-6x的图像上，则y1、y2、y3的大小关系是（ ）
A．y1【变式12-3】（2023秋·辽宁阜新·九年级阜新实验中学校考期末）小明根据学习函数的经验，对函数y=1x-1+1的图象与性质进行了探究．下面是小明的探究过程，请补充完整：
(1)函数y=1x-1+1的自变量x的取值范围是______；
(2)下表列出了y与x的几组对应值，请写出m，n的值：m= ______，n= ______；
(3)在如图所示的平面直角坐标系中，描全上表中以各对对应值为坐标的点，并画出该函数的图象．
(4)结合函数的图象，解决问题：
①方程1x-1+1=x的解为：______
②当函数值1x-1+1>32时，x的取值范围是：______
【题型13 反比例函数与一次函数图象的综合判断】
【例13】（2023春·广东中山·九年级广东省中山市中港英文学校校考期中）已知一次函数y=kx+m（k，m为常数，k≠0）的图像如图所示，则正比例函数y=-kx和反比例函数y=mx在同一坐标系中的图像大致是（ ）
A．B．
C．D．
【变式13-1】（2023春·上海静安·九年级上海市回民中学校考期中）若反比例函数y=kxx>0，y随x增大而增大，则y=kx-2的图像大致是（ ）
A． B． C． D．
【变式13-2】（2023秋·湖南怀化·九年级统考期中）函数y=mx与y=mx-1m≠0在同一平面直角坐标系中的图象可能是（ ）
A． B．
C．D．
【变式13-3】（2023春·江苏苏州·九年级校考期中）如图所示，满足函数y=kx-k和y=kxk≠0的大致图像是（ ）
A．①②B．②③C．②④D．①④
【题型14 反比例函数与一次函数图象的交点问题】
【例14】（2023春·吉林长春·九年级吉林大学附属中学校考期中）如图，在平面直角坐标系中，一次函数y=k1x+bk1≠0的图象与反比例函数y=k2xk2≠0的图象交于Am,2、B-2,-1，与y轴交于点C．

(1)求k1、k2及b的值；
(2)△AOB的面积为______．
【变式14-1】（2023春·河南南阳·九年级统考期中）如图，A、B两点在函数y1=mxx>0的图象上．

(1)求m的值及直线AB的解析式y2=kx+b．
(2)当kx+b≥mxx>0时，自变量x的取值范围是______．
(3)如果一个点的横、纵坐标均为整数，那么我们称这个点为格点，请直接写出图中阴影部分（不包括边界）所含格点的个数．
(4)请在右图中画出函数y3=mx的图象并写出当x=12时y1、y2、y3的大小关系．
【变式14-2】（2023春·江苏淮安·九年级统考期中）如图，将反比例函数y=5x(x>0)的图象绕坐标原点0，0顺时针旋转45°，旋转后的图象与x轴相交于A点，若直线y=12x与旋转后的图象相交于B，则△OAB的面积为 ．

【变式14-3】（2023春·湖南株洲·九年级校考期末）如图，在平面直角坐标系中，一次函数y1=kx+bk≠0的图象与反比例函数y2=mxm≠0的图象相交于第一，三象限内的A3，5，Ba，-3，与x轴交于点C．

(1)求该反比例函数和一次函数的表达式；
(2)在y轴上找一点P使PB-PC最大，求PB-PC的最大值．
【题型15 反比例函数与一次函数图象的实际应用】
【例15】（2023春·江苏宿迁·九年级统考期末）通过实验研究发现：初中生在数学课上听课注意力指标随上课时间的变化而变化，上课开始时，学生兴趣激增，中间一段时间，学生的兴趣保持平稳状态，随后开始分散，学生注意力指标y随时间x分钟）变化的函数图像如图所示，当0≤x<10和10≤x<20时，图像是线段；当20≤x≤45时，图像是反比例函数图像的一部分．

(1)求图中点A的坐标；
(2)王老师在一节数学课上讲解一道数学综合题需要16分钟，他能否经过适当的安排，使学生在听这道综合题讲解时，注意力指标都不低于36？请说明理由．
【变式15-1】（2023秋·吉林通化·九年级统考期末）为了预防“流感”，某学校对教室采用药熏法进行消毒，已知药物燃烧时，室内每立方米空气中的含药量y（毫克）与药物点燃后的时间x（分）满足函数关系式y＝2x，药物点燃后6分钟燃尽，药物燃尽后，校医每隔6分钟测一次空气中含药量，测得数据如下表：
(1)在如图所示平面直角坐标系中描出以表格中数据为坐标的各点；
(2)观察上述各点的分布规律，判断它们是否在同一个反比例函数图象上，如果在同一个反比例函数图象上，求出这个反比例函数图象所对应的函数表达式，如果不在同一个反比例函数图象上，说明理由；
(3)研究表明：空气中每立方米的含药量不低于8毫克，且持续4分钟以上才能有效杀灭空气中的病菌，应用上述发现的规律估算此次消毒能否有效杀灭空气中的病菌？
【变式15-2】（2023秋·河北邢台·九年级校考期末）某品牌热水器中，原有水的温度为20°C，开机通电，热水器启动开始加热（加热过程中水温y°C与开机时间x分钟满足一次函数关系），当加热到80°C时自动停止加热，随后水温开始下降（水温下降过程中水温y°C与开机时间x分钟成反比例函数关系）．当水温降至30°C时，热水器又自动以相同的功率加热至80°C……重复上述过程，如图，根据图像提供的信息，则
（1）当0≤x≤15时，水温y°C开机时间x分钟的函数表达式 ；
（2）当水温为30°C时，t= ；
（3）通电60分钟时，热水器中水的温度y约为 ．
【变式15-3】（2023春·江苏南京·九年级南师附中新城初中校考期末）如图①，有一块边角料ABCDE，其中AB，BC，DE，EA是线段，曲线CD可以看成反比例函数图象的一部分．测量发现：∠A=∠E=90°，AE=5，AB=DE=1，点C到AB，AE所在直线的距离分别为2，4．

(1)小宁把A，B，C，D，E这5个点先描到平面直角坐标系上，记点A的坐标为-1,0；点B的坐标为-1,1．
请你在图②中补全平面直角坐标系并画出图形ABCDE；
(2)求直线BC，曲线CD的函数表达式；
(3)小宁想利用这块边角料截取一个矩形MNQP，其中M，N在AE上（点M在点N左侧），点P在线段BC上，点Q在曲线CD上．若矩形MNQP的面积是53，则PM=________________．
【题型16 反比例函数与一次函数的其他综合运用】
【例16】（2023春·山东济南·九年级统考期末）如图1，点Am,6，B6,1在反比例函数y=kx上，作直线AB，交坐标轴于点M、N，连接OA、OB．

(1)求反比例函数的表达式和m的值；
(2)求△AOB的面积；
(3)如图2，E是线段AB上一点，作AD⊥x轴于点D，过点E作EF∥AD，交反比例函数图象于点F，若EF=13AD，求出点E的坐标．
【变式16-1】（2023春·黑龙江大庆·九年级统考期中）如图，点A1，A2，A3…在反比例函数y=1xx>0的图象上，点B1，B2，B3，…Bn在y轴上，且∠B1OA1=∠B2B1A2=∠B3B2A3=⋅⋅⋅⋅⋅⋅，直线y=x与双曲线y=1x交于点A1，B1A1⊥OA1，B2A2⊥B1A2，B3A3⊥B2A3…，则Bn（n为正整数）的坐标是 ．

【变式16-2】（2023春·江苏苏州·九年级星海实验中学校考期中）【阅读理解】把一个函数图象上每个点的纵坐标变为原来的倒数（原函数图象上纵坐标为0的点除外）、横坐标不变，可以得到另一个函数的图象，我们称这个过程为倒数变换．

【知识运用】如图1，将y=x的图象经过倒数变换后可得到y=1x的图象（部分）．特别地，因为y=x图象上纵坐标为0的点是原点，所以该点不作变换，因此y=1x的图象上也没有纵坐标为0的点．小明在求y=x的图象与y=1x的交点时速用了开平方的定义：y=1xy=x，得x2=1，解得x=±1，则图象交点坐标为1,1或-1,-1．
【拓展延伸】请根据上述阅读材料完成：
(1)请在图2的平面直角坐标系中画出y=x+1的图象和它经过倒数变换后的图象．
(2)设函数y=x+1的图象和它经过倒数变换后的图象的交点为A，B（点A在左边），直接写出其坐标．A______，B______；
(3)设C-1,m，且S△ABC=4，求m．
【变式16-3】（2023春·江苏泰州·九年级统考期末）在学习反比例函数后，小华在同一个平面直角坐标系中画出了y= 9x (x>0)和y=-x+10的图像，两个函数图像交于A(1,9)，B(9,1)两点，在线段AB上选取一点P，过点P作y轴的平行线交反比例函数图像于点Q（如图1），在点P移动的过程中，发现PQ的长度随着点P的运动而变化．为了进一步研究PQ的长度与点P的横坐标之间的关系，小华提出了下列问题：

(1)设点P的横坐标为x，PQ的长度为y，则y与x之间的函数关系式为______(1≤x≤9)；
(2)为了进一步研究（1）中的函数关系，决定运用列表，描点，连线的方法绘制函数的图像：
①列表：
表中m＝______，n＝______；
②描点：根据上表中的数据，在图2中描出各点；
③连线：请在图2中画出该函数的图像．观察函数图像，当x=______时，y的最大值为______．
(3)①已知某矩形的一组邻边长分别为m，n，且该矩形的周长W与n存在函数关系W=-18n+24，求m取最大值时矩形的对角线长．
②如图3，在平面直角坐标系中，直线y=- 23 x-2与坐标轴分别交于点A、B，点M为反比例函数y= 6x (x>0)上的任意一点，过点M作MC⊥x轴于点C，MD⊥y轴于点D．求四边形ABCD面积的最小值．
x
…
-4
-3
-2
-1
0
1
2
3
…
y
…
5
0
-3
-4
-3
0
5
12
…
x
…
-3
0
1
3
5
…
y
…
7
-8
-9
-5
7
…
x
3.23
3.24
3.25
3.26
ax2+bx+c
﹣0.06
﹣0.02
0.03
0.09
x
…
1
2
3
4
5
6
7
8
…
y=ax2+bx+c
…
-1.78
-3.70
-4.42
-3.91
-2.20
0.75
4.88
10.27
…
时间x（分钟）
0
10
…
60
累计车数y（辆）
0
110
…
360
x
…
-32
-1
-12
0
12
32
2
52
3
72
…
y
…
35
m
13
0
-1
n
2
53
32
75
…
药物点燃后的时间x（分）
6
12
18
24
空气中的含药量y（毫克/立方米）
12
6
4
3
x
1
32
2
3
4
92
6
9
y
0
52
m
4
154
72
n
0