考点15 正多边形与圆的6大考点方法归类-【考点通关】2023-2024学年九年级数学上册考点归纳与解题策略（人教版）

这是一份考点15 正多边形与圆的6大考点方法归类-【考点通关】2023-2024学年九年级数学上册考点归纳与解题策略（人教版），共8页。
正多边形概念：各条边相等，并且各个内角也都相等的多边形叫做正多边形．
正多边形的相关概念：
正多边形的中心：正多边形的外接圆的圆心叫做这个正多边形的中心．
正多边形的半径：正多边形外接圆的半径叫做正多边形的半径．
正多边形的中心角：正多边形每一边所对的圆心角叫做正多边形的中心角．
正多边形的边心距：中心到正多边形的一边的距离叫做正多边形的边心距．
半径、边心距，边长之间的关系：
任意的一个多边形（边数大于3）不一定有外接圆和内切圆，但正多边形都有一个外接圆和一个内切圆，且这两个圆是同心圆.
2 正多边形的对称性
所有的正多边形都是轴对称图形，一个正n边形共有n条对称轴，每条对称轴都通过正n边形的中心.当n为偶数时，它还是中心对称图形，它的中心就是对称中心。
3 正多边形的有关计算的公式和方法
(1)正n边形的每个内角为( n -2 )180°/n= 180°-360°n.
(2)正n边形的每个中心角为360°n.
(3)正n边形的每个外角为360°n.
(4)正n边形的半径R、边心距r、边长a之间的关系为(12a)²＋r²＝R²。
(5)正n边形的半径R、边心距r、则正n边形的周长l＝na，面积s＝12arn＝12rl.
在进行与正多边形有关的计算时，通常作正n边形的半径和边心距，把正n边形分成2n个直角三角形，再利用勾股定理即可.
4 构造特殊三角形解正多边形在解决有关正六边形或正方形的计算
可以作相邻两条半径使其与边分别构成等边三角形或等腰直角三角形，然后与前面学过的勾股定理、垂径定理及切线的性质等知识联系起来综合求解。
5 正多边形的外接圆的有关计算方法
半径、边心距与边长的一半构成一个直角三角形，有关正多边形的计算问题都可以转化为直角三角形问题.因此在解决与正多边形有关的线段问题时，常作出半径、边心距构造直角三角形。
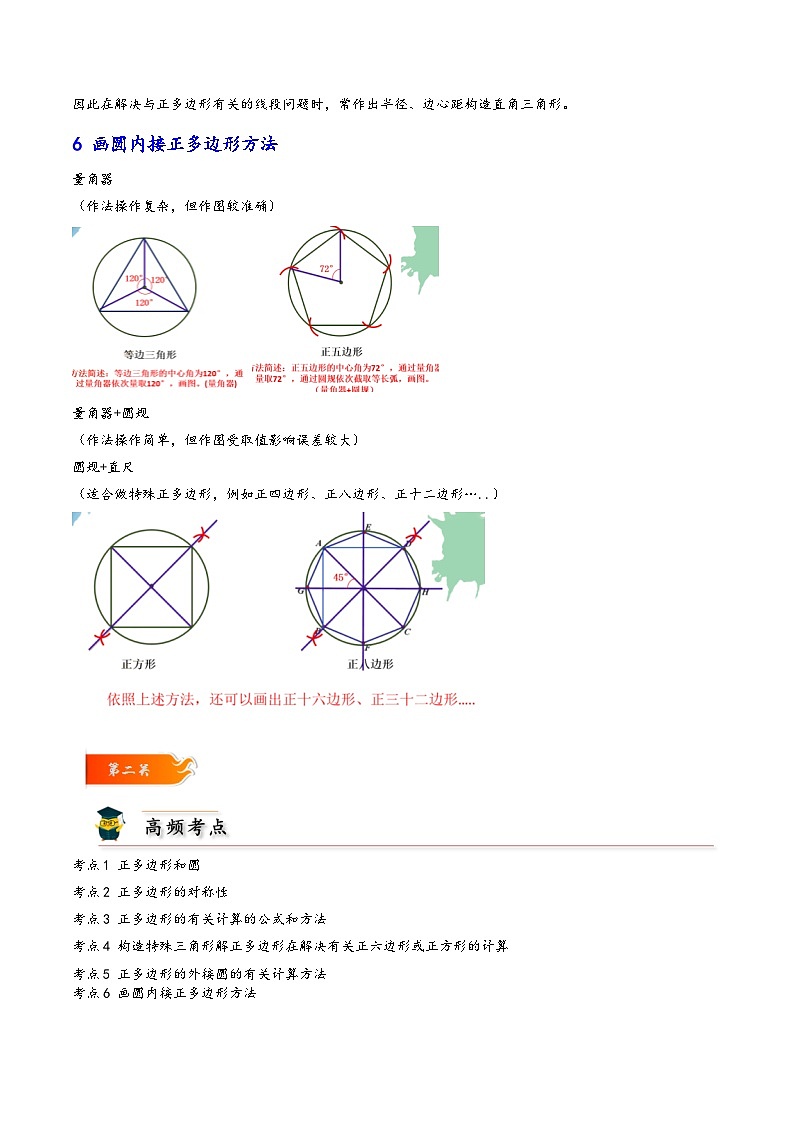
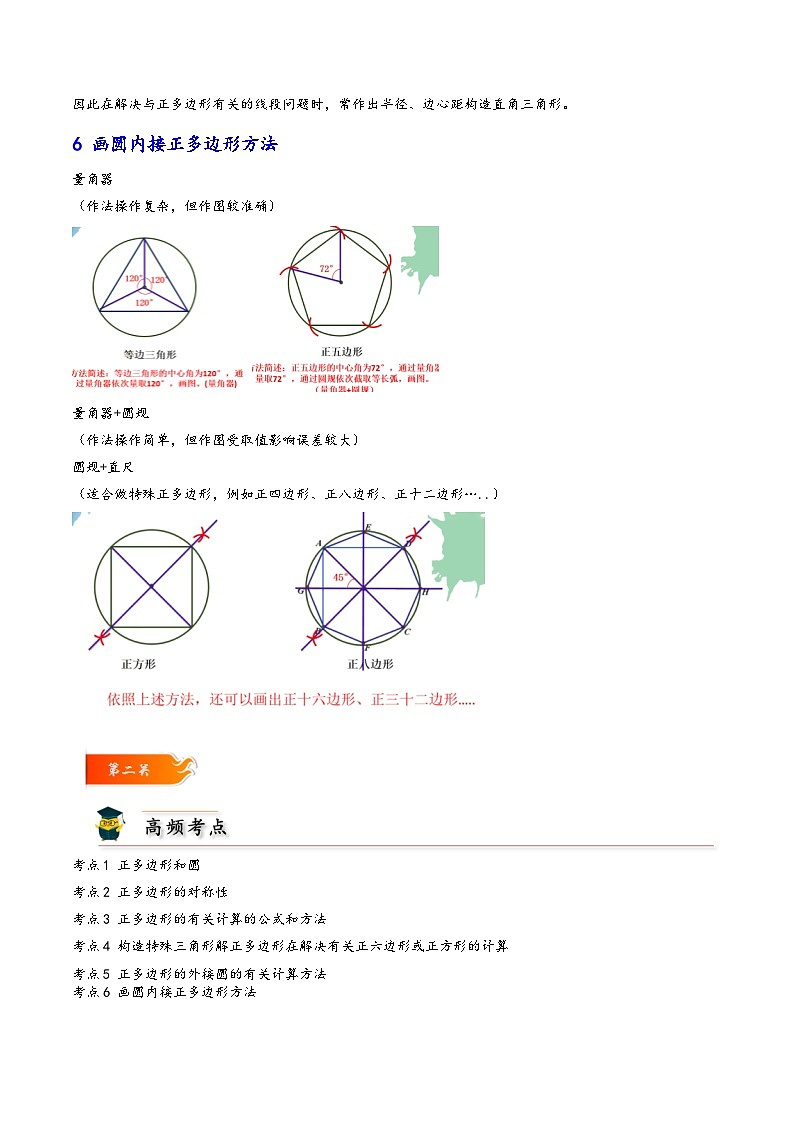
6 画圆内接正多边形方法
量角器
（作法操作复杂，但作图较准确）
量角器+圆规
（作法操作简单，但作图受取值影响误差较大）
圆规+直尺
（适合做特殊正多边形，例如正四边形、正八边形、正十二边形…..）
考点1 正多边形和圆
考点2 正多边形的对称性
考点3 正多边形的有关计算的公式和方法
考点4 构造特殊三角形解正多边形在解决有关正六边形或正方形的计算
考点5 正多边形的外接圆的有关计算方法
考点6 画圆内接正多边形方法
考点1 正多边形和圆
1．（2023秋·山西阳泉·九年级统考期末）如图，正八边形内接于，为弧上的一点（点不与点，重合），则的度数为（ ）

A．B．C．D．
2．（2023秋·全国·九年级专题练习）如图，五边形是的内接正五边形，过点作的切线交的延长线于点，交的延长线于点．则下列结论中正确的是（ ）

A．B．C．D．
3．（2023秋·江苏·九年级专题练习）正六边形的半径为4，则它的边心距是（ ）
A．2B．4C．D．
4．（2023·全国·九年级专题练习）如图，将一张正六边形纸片的阴影部分剪下，拼成一个四边形，若拼成的四边形的面积为S，则纸片的剩余部分的面积为（ ）

A．B．C．D．S
5．（2023春·全国·九年级专题练习）已知正六边形的边长为4，则这个正六边形外接圆的半径为（ ）
A．2B．3C．4D．
考点2 正多边形的对称性
6．（2023春·云南昆明·九年级专题练习）下列命题错误的是（ ）
A．各边相等的圆内接多边形是正多边形B．三角形的内心到它三边的距离相等
C．任何一条直径所在直线都是圆的对称轴D．同弦所对的圆周角相等
7．（2018春·九年级课时练习）顺次连接正六边形的三个不相邻的顶点，得到如图的图形，下列说法错误的是（ ）
A．△ACE是等边三角形B．既是轴对称图形也是中心对称图形
C．连接AD，则AD分别平分∠EAC与∠EDCD．图中一共能画出3条对称轴
8．（2023·江苏无锡·统考中考真题）下列命题：①各边相等的多边形是正多边形；②正多边形是中心对称图形；③正六边形的外接圆半径与边长相等；④正n边形共有n条对称轴．其中真命题的个数是（ ）
A．4B．3C．2D．1
9．（2023春·九年级课时练习）如图是一个正八边形，则它（ ）
A．只是轴对称图形B．只是中心对称图形
C．既是轴对称图形，也是中心对称图形D．既不是轴对称图形，也不是中心对称图形
10．（2023·江苏·九年级专题练习）下列关于正多边形的叙述，正确的是（ ）
A．正七边形既是轴对称图形又是中心对称图形B．存在一个正多边形，它的外角和为
C．任何正多边形都有一个外接圆D．不存在每个外角都是对应每个内角两倍的正多边形
考点3 正多边形的有关计算的公式和方法
11．（2023秋·全国·九年级专题练习）正八边形的中心角的度数是（ ）
A．30°B．45°C．60°D．90°
12．（2022秋·广西河池·九年级统考期末）如图，已知正五边形内接于，则的度数是（ ）
A．B．C．D．
13．（2023·四川成都·模拟预测）如图，多边形是的内接正n边形，已知的半径为r，的度数为，点O到的距离为d，的面积为S．下面三个推断中．
①当n变化时，随n的变化而变化，与n满足的函数关系是反比例函数关系；
②若为定值，当r变化时，d随r的变化而变化，d与r满足的函数关系是正比例函数关系；
③若n为定值，当r变化时，S随r的变化而变化，S与r满足的函数关系是二次函数关系．
其中正确的是（ ）
A．①②B．①③C．②③D．①②③
14．（2023秋·辽宁沈阳·九年级沈阳市第七中学校考期末）在圆内接正六边形中，正六边形的边长为，则这个正六边形的中心角和边心距分别是（ ）
A．，B．，C．，D．，
15．（2023秋·全国·九年级专题练习）如图，点、、、为一个正多边形的顶点，点为正多边形的中心，若，则这个正多边形的边数为（ ）
A．5B．10C．12D．20
考点4 构造特殊三角形解正多边形在解决有关正六边形或正方形的计算
16．（2023春·天津和平·九年级专题练习）如图，六边形是正六边形，点是边的中点，，分别与交于点，，则的值为（ ）．
A．B．C．D．
17．（2022秋·全国·九年级专题练习）如图，有一张菱形纸片，分别把沿着两条平行于的直线进行对折，得到一个六边形，如果这个六边形是正六边形，则菱形的对角线长的比（ ）
A．B．C．D．
18．（2023·河北·模拟预测）周长相等的正方形与正六边形的面积分别为、，和的关系为（ ）
A．B．C．D．
19．（2023秋·湖北十堰·九年级统考期末）如图，和分别为内接正方形，正六边形和正n边形的一边，则n是（ ）．
A．六B．八C．十D．十二
20．（2022春·九年级课时练习）如图，点，，在上，若，，分别是内接正三角形．正方形，正边形的一边，则（ ）
A．9B．10C．12D．15
考点5 正多边形的外接圆的有关计算方法
21．（2023秋·江苏·九年级专题练习）若一个正六边形的边长为2，则其外接圆与内切圆的半径分别为（ ）
A．2，1B．2，C．，2D．，3
22．（2023秋·江苏·九年级专题练习）如图，是正方形的外接圆，若的半径为2，则正方形的边长为（ ）
A．1B．C．D．
23．（2021秋·浙江衢州·九年级校考期中）如图，边长为4的正三角形外接圆，以其各边为直径作半圆，则图中阴影部分面积为（ ）
A．12+2πB．4+πC．24+2πD．12+14π
24．（2020秋·福建厦门·九年级校考阶段练习）如图，⊙O是正六边形ABCDEF的外接圆，⊙O的半径长为a，下列说法中不正确的是（ ）
A．正六边形ABCDEF的中心角等于60°B．正六边形ABCDEF的周长等于6a
C．正六边形ABCDEF的边心距等于D．正六边形ABCDEF的面积等于3
25．（2022·天津和平·统考一模）如图，⊙O是正方形ABCD与正六边形AEFCGH的外接圆．则正方形ABCD与正六边形AEFCGH的周长之比为（ ）
A．∶ 3B．∶1C．∶D．1∶
考点6画圆内接正多边形方法
26．（2023·江苏·九年级假期作业）如图，已知AC为的直径．请用尺规作图法，作出的内接正方形ABCD．（保留作图痕迹．不写作法）
27．（2023·江苏·九年级假期作业）请用圆规和直尺作图，不写作法，但要保留作图痕迹．
已知：⊙O，点A在圆上．
求作：以A为一顶点作圆内接正方形ABCD．
28．（2022·广东深圳·统考一模）如图，已知，点在圆上，请以为一顶点作圆内接正方形．（保留作图痕迹，不写作法）
29．（2021秋·全国·九年级专题练习）请用无刻度直尺完成下列作图，不写画法，保留画图痕迹（用虚线表示画图过程，实线表示画图结果）．
（1）如图1，E是平行四边形ABCD边AD上一点，过点A画一条直线，使其与EC平行；
（2）如图2，正六边形ABCDEF（六边相等，六角相等的六边形），在图中画一条直线，使其垂直平分AF；
（3）如图3，⊙O是四边形ABCD的外接圆，且AB＝BC＝CD，在图中画一条异于BC的直线，使其与AD平行．
30．（2023·江苏·九年级假期作业）如图1，等边内接于⊙O，连接CO并延长交⊙O于点D．
（1）可以证明CD垂直平分AB，写出与的数量关系：___．
（2）请你仅使用无刻度的直尺按要求作图：
①在图1中作出一个正六边形，保留作图痕迹（作图过程用虚线表示，作图结果用实线表示）．
②请在图2中作出⊙O的内接正六边形ADBECF的一条不经过顶点的对称轴，保留作图痕迹(作图过程用虚线表示，作图结果用实线表示）．