四川省泸州市江阳区习之学校2023-2024学年八年级上学期10月月考数学试卷

这是一份四川省泸州市江阳区习之学校2023-2024学年八年级上学期10月月考数学试卷，共5页。
A．2B．5C．10D．11
2．（3分）如图所示，△AOC≌△BOD，C，D是对应点（ ）
A．∠A与∠B是对应角B．∠AOC与∠BOD是对应角
C．OC与OB是对应边D．OC与OD是对应边
3．（3分）如图，直线AB∥CD，且AC⊥CB于点C，则∠BCD的度数为（ ）
A．65°B．55°C．45°D．35°
4．（3分）若△ABC中，∠A：∠B：∠C＝5：3：2，则△ABC是（ ）
A．锐角三角形B．直角三角形
C．钝角三角形D．任意三角形
5．（3分）一副三角板如图所示摆放，若∠1＝80°，则∠2的度数是（ ）
A．80°B．95°C．100°D．110°
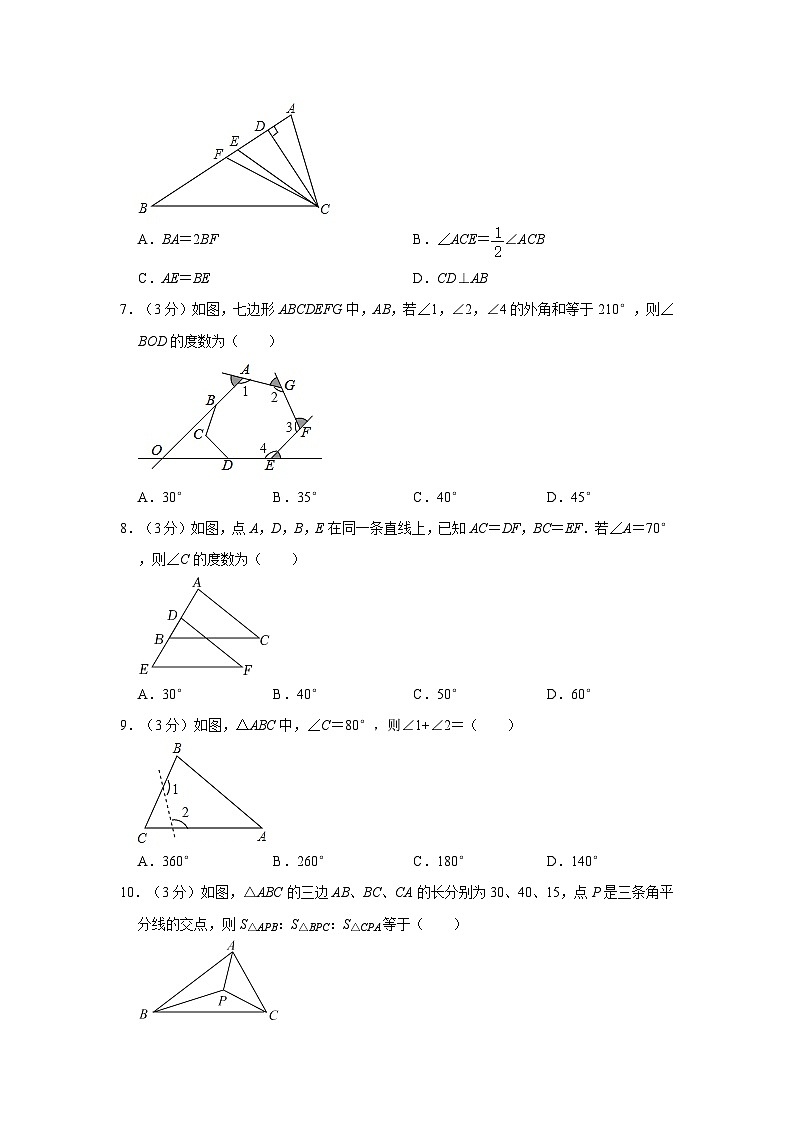
6．（3分）如图，CD、CE、CF分别是△ABC的高、角平分线、中线，则下列各式中错误的是（ ）
A．BA＝2BFB．∠ACE＝∠ACB
C．AE＝BED．CD⊥AB
7．（3分）如图，七边形ABCDEFG中，AB，若∠1，∠2，∠4的外角和等于210°，则∠BOD的度数为（ ）
A．30°B．35°C．40°D．45°
8．（3分）如图，点A，D，B，E在同一条直线上，已知AC＝DF，BC＝EF．若∠A＝70°，则∠C的度数为（ ）
A．30°B．40°C．50°D．60°
9．（3分）如图，△ABC中，∠C＝80°，则∠1+∠2＝（ ）
A．360°B．260°C．180°D．140°
10．（3分）如图，△ABC的三边AB、BC、CA的长分别为30、40、15，点P是三条角平分线的交点，则S△APB：S△BPC：S△CPA等于（ ）
A．1：1：1B．6：8：3C．5：8：3D．4：5：3
11．（3分）已知△ABC的三条边分别为a，b，c，化简|a+b﹣c|﹣|b﹣a﹣c|+|a﹣b+c|（ ）
A．3a﹣b+cB．a+b﹣cC．a﹣b﹣cD．﹣a+3b﹣3c
12．（3分）如图，在△AOB和△COD中，OA＝OB，OA＜OC，∠AOB＝∠COD＝36°．连接AC，连接OM．则在下列结论：①∠AMB＝36°，②AC＝BD，④∠AMD＝144°．其中正确的结论个数有（ ）个．
A．4B．3C．2D．1
二.填空题（共4小题，每题3分）
13．（3分）如图，点B，F，C，E在一条直线上，AC∥FD，要使△ABC≌△DEF，则这个条件可以是 ，根据你添加的条件证明全等的依据是 ．
14．（3分）如图，在△ABC中，∠ACB＝90°，若AB：AC＝3：2，且BD＝2 ．
15．（3分）为庆祝中国共产党建党100周年，某校用红色灯带制作了一个如图所示的正五角星（A，B，C，D，E是正五角星的五个顶点），则图中∠A的度数是 度．
16．（3分）如图，在Rt△ABC中，∠A＝90°，S△BDC＝12，BC＝8，则AD＝ ．
三.解答题（17-19题.每题6分：20-21题，每题7分：22-23题，每题8分；24-25题每题12分）
17．（6分）计算：．
18．（6分）填空：把下面的推理过程补充完整，并在括号内注明理由．
已知：如图，BC∥EF，AB＝DE，试说明∠C＝∠F．
解：∵BC∥EF（已知）
∴∠ABC＝ （ ）
在△ABC与△DEF中
AB＝DE


∴△ABC≌△DEF（ ）．
∴∠C＝∠F（ ）．
19．（6分）已知：如图，AC＝BD，AD＝BC
20．（7分）如图，已知AD＝AB，AC＝AE，连接DC，BE．
（1）求证：△BAE≌△DAC；
（2）若∠CAD＝143°，∠D＝15°，求∠E的度数．
21．（7分）如图，在△ABC和△DBC中，∠ACB＝∠DBC＝90°，DE⊥AB，垂足为点F
（1）求证：BD＝BC；
（2）若BD＝6cm，求AC的长．
22．（8分）如图，在△ABC中，D为AB上一点，连接DE并延长至点F，使得EF＝ED
（1）求证：CF∥AB；
（2）若∠ABC＝50°，连接BE，BE平分∠ABC，求∠A的度数．
23．（8分）已知：如图，点B，C，E在同一条直线上，∠DBM＝∠DAN，DM⊥BE于M
（1）求证：△BDM≌△ADN；
（2）若AC＝7，BC＝3，求CM的长．
24．（12分）在△ABC中，AE、BF是角平分线，交于O点．
（1）如图1，AD是高，∠BAC＝50°，求∠DAC和∠BOA的度数．
（2）如图2，若OE＝OF，AC≠BC
（3）如图3，若∠C＝90°，BC＝8，AB＝10，求S△AOB．
25．（12分）问题背景：
如图1：在四边形ABCD中，AB＝AD，∠BAD＝120°，F分别是BC，CD上的点．且∠EAF＝60°．探究图中线段BE，FD之间的数量关系．
（1）小王同学探究此问题的方法是：延长FD到点G．使DG＝BE．连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，他的结论应是 ；（并写出证明过程）
探索延伸：
（2）如图2，若在四边形ABCD中，AB＝AD，F分别是BC，CD上的点∠BAD，上述结论是否仍然成立
2023-2024学年四川省泸州市江阳区习之学校八年级（上）月考数学试卷（10月份）
参考答案与试题解析
一.选择题（共12小题，
1．（3分）若长度是4，6，a的三条线段能组成一个三角形，则a的值可以是（ ）
A．2B．5C．10D．11
【答案】B
【分析】根据三角形三边关系定理得出6﹣4＜a＜6+4，求出2＜a＜10，再逐个判断即可．
【解答】解：∵长度是4，6，a的三条线段能组成一个三角形，
∴5﹣4＜a＜6+8，
∴2＜a＜10，
∴只有选项B符合题意，选项A、选项D都不符合题意；
故选：B．
【点评】本题考查了三角形的三边关系定理，能熟记三角形的三边关系定理是解此题的关键，注意：三角形的任意两边之和都大于第三边，三角形的两边之差小于第三边．
2．（3分）如图所示，△AOC≌△BOD，C，D是对应点（ ）
A．∠A与∠B是对应角B．∠AOC与∠BOD是对应角
C．OC与OB是对应边D．OC与OD是对应边
【答案】C
【分析】根据全等三角形的性质进行判断即可．
【解答】解：∵△AOC≌△BOD，
∴∠A＝∠B，∠AOC＝∠BOD，
故选：C．
【点评】本题考查了全等三角形的性质的应用，注意：全等三角形的对应角相等，对应边相等．
3．（3分）如图，直线AB∥CD，且AC⊥CB于点C，则∠BCD的度数为（ ）
A．65°B．55°C．45°D．35°
【答案】B
【分析】由三角形内角和定理可求∠ABC的度数，由平行线的性质可求解．
【解答】解：∵AC⊥CB，
∴∠ACB＝90°，
∴∠ABC＝180°﹣90°﹣∠BAC＝90°﹣35°＝55°，
∵直线AB∥CD，
∴∠ABC＝∠BCD＝55°，
故选：B．
【点评】本题考查了平行线的性质，垂线的性质，三角形内角和定理，掌握平行线的性质是本题的关键．
4．（3分）若△ABC中，∠A：∠B：∠C＝5：3：2，则△ABC是（ ）
A．锐角三角形B．直角三角形
C．钝角三角形D．任意三角形
【答案】B
【分析】可设三角形的三个内角的度数分别为：5x，3x，2x，再由三角形的内角和进行求解，即可判断三角形的类型．
【解答】解：设三角形的三个内角的度数分别为：5x，3x，依题意得：
8x+3x+2x＝180°，
解得：x＝18°，
∴∠A＝4x＝5×18°＝90°，
∴△ABC是直角三角形．
故选：B．
【点评】本题主要考查三角形的内角和定理，解答的关键是明确三角形的内角和为180°．
5．（3分）一副三角板如图所示摆放，若∠1＝80°，则∠2的度数是（ ）
A．80°B．95°C．100°D．110°
【答案】B
【分析】根据直角三角形的性质求出∠5，根据三角形的外角性质求出∠3，根据对顶角相等求出∠4，再根据三角形的外角性质计算，得到答案．
【解答】解：如图，∠5＝90°﹣30°＝60°，
∴∠4＝∠2＝35°，
∴∠2＝∠4+∠4＝95°，
故选：B．
【点评】本题考查的是三角形的外角性质、直角三角形的性质，掌握三角形的一个外角等于和它不相邻的两个内角的和是解题的关键．
6．（3分）如图，CD、CE、CF分别是△ABC的高、角平分线、中线，则下列各式中错误的是（ ）
A．BA＝2BFB．∠ACE＝∠ACB
C．AE＝BED．CD⊥AB
【答案】C
【分析】从三角形的一个顶点向它的对边作垂线，垂足与顶点之间的线段叫做三角形的高．
三角形一个内角的平分线与这个内角的对边交于一点，则这个内角的顶点与所交的点间的线段叫做三角形的角平分线．
三角形一边的中点与此边所对顶点的连线叫做三角形的中线．依此即可求解．
【解答】解：∵CD，CE、角平分线，
∴CD⊥AB，∠ACE＝，AB＝8BF．
故选：C．
【点评】本题考查了三角形的角平分线、中线和高，熟练掌握它们的定义和性质是解题的关键．
7．（3分）如图，七边形ABCDEFG中，AB，若∠1，∠2，∠4的外角和等于210°，则∠BOD的度数为（ ）
A．30°B．35°C．40°D．45°
【答案】A
【分析】由外角和内角的关系可求得∠1、∠2、∠3、∠4的和，由五边形内角和可求得五边形OAGFE的内角和，则可求得∠BOD．
【解答】解：∵∠1、∠2、∠4的外角的角度和为210°，
∴∠1+∠2+∠8+∠4+210°＝4×180°，
∴∠4+∠2+∠3+∠6＝510°，
∵五边形OAGFE内角和＝（5﹣2）×180°＝540°，
∴∠4+∠2+∠3+∠5+∠BOD＝540°，
∴∠BOD＝540°﹣510°＝30°，
故选：A．
【点评】本题主要考查多边形的内角和，利用内角和外角的关系求得∠1、∠2、∠3、∠4的和是解题的关键．
8．（3分）如图，点A，D，B，E在同一条直线上，已知AC＝DF，BC＝EF．若∠A＝70°，则∠C的度数为（ ）
A．30°B．40°C．50°D．60°
【答案】C
【分析】利用SSS证明△ABC≌△DEF可得∠ABC＝∠E＝60°，再根据三角形内角和定理即可解决问题．
【解答】解：∵AD＝BE，
∴AD+BD＝BE+BD，
∴AB＝DE，
在△ABC和△DEF中，
，
∴△ABC≌△DEF（SSS），
∴∠ABC＝∠E＝60°，
∵∠A＝70°，
∴∠C＝180°﹣70°﹣60°＝50°．
故选：C．
【点评】本题考查了全等三角形的判定与性质，解决本题的关键是得到△ABC≌△DEF．
9．（3分）如图，△ABC中，∠C＝80°，则∠1+∠2＝（ ）
A．360°B．260°C．180°D．140°
【答案】B
【分析】先利用三角形内角与外角的关系，得出∠1+∠2＝∠C+（∠C+∠3+∠4），再根据三角形内角和定理即可得出结果．
【解答】解：∵∠1、∠2是△CDE的外角，
∴∠2＝∠4+∠C，∠2＝∠5+∠C，
即∠1+∠2＝∠C+（∠C+∠5+∠4）＝80°+180°＝260°．
故选：B．
【点评】此题主要考查了三角形内角和定理及外角的性质，三角形内角和是180°；三角形的任一外角等于和它不相邻的两个内角之和．
10．（3分）如图，△ABC的三边AB、BC、CA的长分别为30、40、15，点P是三条角平分线的交点，则S△APB：S△BPC：S△CPA等于（ ）
A．1：1：1B．6：8：3C．5：8：3D．4：5：3
【答案】B
【分析】由角平分线的性质可得，点P到三角形三边的距离相等，即三个三角形的AB、BC、AC的高相等，利用面积公式即可求解．
【解答】解：过点P作PD⊥BC于D，PE⊥AC于E，
∵P是三角形三条角平分线的交点，
∴PD＝PE＝PF，
∵AB＝30，BC＝40，
∴S△APB：S△BPC：S△CPA＝30：40：15＝6：8：8．
故选：B．
【点评】此题主要考查角平分线的性质和三角形面积的求法，难度不大，熟记角平分线的性质并作出合理的辅助线是解题的关键．
11．（3分）已知△ABC的三条边分别为a，b，c，化简|a+b﹣c|﹣|b﹣a﹣c|+|a﹣b+c|（ ）
A．3a﹣b+cB．a+b﹣cC．a﹣b﹣cD．﹣a+3b﹣3c
【答案】B
【分析】根据三角形的任意两边之和大于第三边可得a+b﹣c＞0，b﹣a+c＞0，b﹣a﹣c＜0，再根据绝对值的性质去掉绝对值符号，然后利用整式的加减运算进行计算即可得解．
【解答】解：∵a、b、c分别为△ABC的三边长，
∴a+b﹣c＞0，b﹣a﹣c＜0，
∴|a+b﹣c|﹣|b﹣a﹣c|+|a﹣b+c|
＝a+b﹣c﹣（a+c﹣b）+a﹣b+c
＝a+b﹣c﹣a﹣c+b+a﹣b+c
＝a+b﹣c．
故选：B．
【点评】本题考查了三角形的三边关系，绝对值的性质，整式的加减运算，熟记性质并去掉绝对值符号是解题的关键．
12．（3分）如图，在△AOB和△COD中，OA＝OB，OA＜OC，∠AOB＝∠COD＝36°．连接AC，连接OM．则在下列结论：①∠AMB＝36°，②AC＝BD，④∠AMD＝144°．其中正确的结论个数有（ ）个．
A．4B．3C．2D．1
【答案】B
【分析】先证明△OAC≌△OBD，所以∠OAC＝∠OBD，AC＝BD，则可对②进行判断；利用三角形内角和得到∠AMB＝∠AOB＝36°，则可对①进行判断，利用邻补角的定义可对④进行判断；过O点作OE⊥AC于E，OF⊥BD于F，如图，根据全等三角形的性质得到OE＝OF，则根据角平分线的性质定理的逆定理得到MO平分∠AMD，然后根据三角形内角和可判断∠AOM≠∠DOM，于是可对③进行判断．
【解答】解：∵∠AOB＝∠COD＝36°，
∴∠AOB+∠BOC＝∠BOC+∠COD，
即∠AOC＝∠BOD，
在△OAC和△OBD中，
，
∴△OAC≌△OBD（SAS），
∴∠OAC＝∠OBD，AC＝BD；
∵∠AOB+∠OAC+∠1＝∠AMB+∠OBD+∠2，
而∠5＝∠2，
∴∠AMB＝∠AOB＝36°，所以①正确；
∴∠AMD＝180°﹣∠AMB＝180°﹣36°＝144°，所以④正确；
过O点作OE⊥AC于E，OF⊥BD于F，
∵△OAC≌△OBD，
∴OE＝OF，
∴MO平分∠AMD，
而∠OAM≠ODM，
∴∠AOM≠∠DOM，所以③错误．
故选：B．
【点评】本题考查了全等三角形的判定与性质：全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具．证明△OAC与△OBD全等是解决问题的关键．
二.填空题（共4小题，每题3分）
13．（3分）如图，点B，F，C，E在一条直线上，AC∥FD，要使△ABC≌△DEF，则这个条件可以是 AB＝ED ，根据你添加的条件证明全等的依据是 AAS ．
【答案】AB＝ED；AAS．
【分析】根据AB∥ED，AC∥FD得到∠B＝∠E，∠ACB＝∠DFE，只需添加一组相等的对应边即可．
【解答】解：添加的条件是：AB＝ED．证明如下：
∵AB∥ED，AC∥FD，
∴∠B＝∠E，∠ACB＝∠DFE，
在△ABC与△DEF中，
，
∴△ABC≌△DEF（AAS）．
故答案为：AB＝ED；AAS．
【点评】本题考查了三角形全等的判定，熟练掌握三角形全等的判定定理是解题的关键．
14．（3分）如图，在△ABC中，∠ACB＝90°，若AB：AC＝3：2，且BD＝2 ．
【答案】．
【分析】过点D作DE⊥AB于点E，则DE＝DC，利用面积法可得出＝，结合AB：AC＝3：2，且BD＝2，可求出CD的长，此题得解．
【解答】解：过点D作DE⊥AB于点E，如图所示.
∵AD平分∠BAC，∠ACB＝90°，
∴DE＝DC．
∵S△ABD＝AC•BD＝，S△ACD＝AC•CD，
∴＝＝，即＝，
∴CD＝，
∴点D到直线AB的距离为．
故答案为：．
【点评】本题考查了角平分线的性质以及三角形的面积，利用面积法，找出＝是解题的关键．
15．（3分）为庆祝中国共产党建党100周年，某校用红色灯带制作了一个如图所示的正五角星（A，B，C，D，E是正五角星的五个顶点），则图中∠A的度数是 36 度．
【答案】36．
【分析】正五角星中，五边形FGHMN是正五边形，根据正多边形及邻补角的性质，即可求得∠AFN＝∠ANF＝72°，然后根据三角形的内角和定理可求得∠A的度数．
【解答】解：如图，
∵正五角星中，五边形FGHMN是正五边形，
∴∠GFN＝∠FNM＝＝108°，
∴∠AFN＝∠ANF＝180°﹣∠GFN＝180°﹣108°＝72°，
∴∠A＝180°﹣∠AFN﹣∠ANF＝180°﹣72°﹣72°＝36°．
故答案为：36．
【点评】本题考查了多边形的内角与外角，正确理解五边形FGHMN是正五边形是解题关键．
16．（3分）如图，在Rt△ABC中，∠A＝90°，S△BDC＝12，BC＝8，则AD＝ 3 ．
【答案】3．
【分析】过D点作DE⊥BC，垂足为E，由已知S△BDC＝12，BC＝8，可求DE，再利用角平分线性质证明AD＝DE即可．
【解答】解：过D点作DE⊥BC，垂足为E，
由S△BDC＝12得BC×DE＝12，
解得DE＝3，
∵BD平分∠ABC，∠A＝90°，
∴AD＝DE＝3．
故答案为：3．
【点评】本题考查了角平分线的性质及三角形面积公式的灵活运用．正确作出辅助线是解答本题的关键．
三.解答题（17-19题.每题6分：20-21题，每题7分：22-23题，每题8分；24-25题每题12分）
17．（6分）计算：．
【答案】﹣．
【分析】先化简各式，然后再进行计算即可解答．
【解答】解：
＝﹣3﹣4+3﹣﹣（﹣2）
＝﹣1﹣3+3﹣+5
＝﹣．
【点评】本题考查了实数的运算，准确熟练地进行计算是解题的关键．
18．（6分）填空：把下面的推理过程补充完整，并在括号内注明理由．
已知：如图，BC∥EF，AB＝DE，试说明∠C＝∠F．
解：∵BC∥EF（已知）
∴∠ABC＝ ∠DEF （ 两直线平行，同位角相等 ）
在△ABC与△DEF中
AB＝DE
∠ABC＝∠DEF
BC＝EF
∴△ABC≌△DEF（ SAS ）．
∴∠C＝∠F（ 全等三角形的对应角相等 ）．
【答案】见试题解答内容
【分析】由于BC∥EF，所以∠ABC＝∠DEF的根据是两直线平行，同位角相等，然后再根据已知条件，判定三角形全等，利用全等三角形的性质，求出∠C＝∠F．
【解答】解：∵BC∥EF（已知），
∴∠ABC＝∠DEF（两直线平行，同位角相等），
在△ABC与△DEF中，
AB＝DE，
∠ABC＝∠E，
BC＝EF，
∴△ABC≌△DEF（SAS），
∴∠C＝∠F（全等三角形的对应角相等）．
【点评】本题主要考查了平行线的性质，平行线的性质定理是证明角相等的重要依据．
19．（6分）已知：如图，AC＝BD，AD＝BC
【答案】证明见解析．
【分析】连接AB，利用SSS证明△ADB与△BCA全等，进而利用全等三角形的性质解答即可．
【解答】证明：连接AB，
在△ADB和△BCA中，
，
∴△ADB≌△BCA（SSS），
∴∠D＝∠C．
【点评】本题考查了全等三角形的性质和判定，关键是利用SSS证明△ADB与△BCA全等解答．
20．（7分）如图，已知AD＝AB，AC＝AE，连接DC，BE．
（1）求证：△BAE≌△DAC；
（2）若∠CAD＝143°，∠D＝15°，求∠E的度数．
【答案】（1）答案见解析；
（2）22°．
【分析】（1）根据题意由∠DAB+∠BAC＝∠CAE+∠BAC，可得∠DAC＝∠BAE，即可求证；
（2）由△BAE≌△DAC，可得∠E＝∠C，再由内角和为180°即可求解．
【解答】（1）证明：∵∠DAB＝∠CAE，
∴∠DAB+∠BAC＝∠CAE+∠BAC，
∴∠DAC＝∠BAE，
在△BAE和△DAC中，
，
∴△BAE≌△DAC （SAS）；
（2）解：∵△BAE≌△DAC，
∴∠E＝∠C，
∵∠CAD＝143°，∠D＝15°，
∴∠C＝180°﹣（∠CAD+∠D）＝22°，
∴∠E＝22°．
【点评】本题主要考查了全等三角形的判定与性质，熟练掌握全等三角形判定的条件是解决问题的关键．
21．（7分）如图，在△ABC和△DBC中，∠ACB＝∠DBC＝90°，DE⊥AB，垂足为点F
（1）求证：BD＝BC；
（2）若BD＝6cm，求AC的长．
【答案】见试题解答内容
【分析】（1）欲证明BD＝BC，只要证明△ABC≌△EDB即可．
（2）由E是BC中点，BD＝6cm，BD＝BC，推出BE＝BC＝BD＝3cm，由△ABC≌△EDB，得到AC＝BE，即可解决问题．
【解答】（1）证明：∵DE⊥AB，
∴∠BFE＝90°，
∴∠ABC+∠DEB＝90°，
∵∠ACB＝90°，
∴∠ABC+∠A＝90°，
∴∠A＝∠DEB，
在△ABC和△EDB中，
，
∴△ABC≌△EDB，
∴BD＝BC．
（2）解：∵E是BC中点，BD＝6cm，
∴BE＝BC＝，
∵△ABC≌△EDB，
∴AC＝BE＝8cm．
【点评】本题考查全等三角形的判定和性质，解题的关键是正确寻找全等三角形，利用全等三角形的性质解决问题，属于中考常考题型．
22．（8分）如图，在△ABC中，D为AB上一点，连接DE并延长至点F，使得EF＝ED
（1）求证：CF∥AB；
（2）若∠ABC＝50°，连接BE，BE平分∠ABC，求∠A的度数．
【答案】（1）证明见解答过程；
（2）65°．
【分析】（1）求出△AED≌△CEF，根据全等三角形的性质得出∠A＝∠ACF，根据平行线的判定得出即可；
（2）根据（1）求出∠A＝∠ACB，根据三角形内角和定理求出即可．
【解答】（1）证明：∵E为AC中点，
∴AE＝CE，
在△AED和△CEF中，
，
∴△AED≌△CEF（SAS），
∴∠A＝∠ACF，
∴CF∥AB；
（2）解：∵AC平分∠BCF，
∴∠ACB＝∠ACF，
∵∠A＝∠ACF，
∴∠A＝∠ACB，
∵∠A+∠ABC+∠ACB＝180°，∠ABC＝50°，
∴2∠A＝130°，
∴∠A＝65°．
【点评】本题考查了全等三角形的性质和判定、平行线的性质和判定、三角形内角和定理等知识点，能综合运用定理进行推理是解此题的关键．
23．（8分）已知：如图，点B，C，E在同一条直线上，∠DBM＝∠DAN，DM⊥BE于M
（1）求证：△BDM≌△ADN；
（2）若AC＝7，BC＝3，求CM的长．
【答案】（1）证明见解析；
（2）2．
【分析】（1）由角平分线的性质可得DM＝DN，再由AAS即可证得△BDM≌△ADN；
（2）由HL证Rt△DCN≌Rt△DCM，得CM＝CN，再由△BDM≌△ADN得BM＝AN，则AC＝AN+CN＝BM+CM＝BC+CM+CM＝BC+2CM，即可得出结果．
【解答】（1）证明：∵CD平分∠ACE，DM⊥BE，
∴DM＝DN，∠DMB＝∠DNA＝90°，
在△BDM和△ADN中，
，
∴△BDM≌△ADN（AAS）；
（2）解：在Rt△DCN和Rt△DCM中，
，
∴Rt△DCN≌Rt△DCM（HL），
∴CM＝CN，
∵△BDM≌△ADN，
∴BM＝AN，
∵AC＝AN+CN＝BM+CM＝BC+CM+CM＝7，
∴3+3CM＝7，
∴CM＝2．
【点评】本题考查了全等三角形的判定和性质、角平分线的性质等知识，熟练掌握全等三角形的判定与性质是解题的关键．
24．（12分）在△ABC中，AE、BF是角平分线，交于O点．
（1）如图1，AD是高，∠BAC＝50°，求∠DAC和∠BOA的度数．
（2）如图2，若OE＝OF，AC≠BC
（3）如图3，若∠C＝90°，BC＝8，AB＝10，求S△AOB．
【答案】见试题解答内容
【分析】（1）根据垂直的定义得到∠ADC＝90°，根据角平分线的定义得到∠ABO＝30°，根据三角形的内角和即可得到结论；
（2）连接OC，根据角平分线的性质得到OM＝ON，根据全等三角形的性质得到∠EOM＝∠FOH，根据角平分线的定义即可得到结论；
（3）连接OC，过O作OD⊥AB于D，OG⊥BC于G，OH⊥AC于H，根据角平分线的性质得到OD＝OG＝OH，根据三角形的面积公式即可得的结论．
【解答】解：（1）∵AD⊥BC，
∴∠ADC＝90°，
∵∠C＝70°，
∴∠DAC＝180°﹣90°﹣70°＝20°；
∵∠BAC＝50°，∠C＝70°，
∴∠BAO＝25°，∠ABC＝60°，
∵BF是∠ABC的角平分线，
∴∠ABO＝30°，
∴∠BOA＝180°﹣∠BAO﹣∠ABO＝180°﹣25°﹣30°＝125°；
（2）连接OC，
∵AE、BF是角平分线，
∴OC是∠ACB的角平分线，
∴∠OCF＝∠OCE，
过O作OM⊥BC，ON⊥AC，
则OM＝ON，
在Rt△OEM与Rt△OFN中，，
∴Rt△OEM≌Rt△OFN，（HL），
∴∠EOM＝∠FON，
∴∠MON＝∠EOF＝180°﹣∠ACB，
∵AE、BF是角平分线，
∴∠AOB＝90°+∠ACB，
即90°+∠ACB＝180°﹣∠ACB，
∴∠ACB＝60°；
（3）连接OC，过O作OD⊥AB于D，OH⊥AC于H，
∵AE、BF是角平分线，
∴OD＝OG＝OH，
∴S△ABC＝×8×6＝6×OG+，
∴OD＝2，
∴S△AOB＝10×2＝10．
【点评】本题考查了全等三角形的判定和性质，角平分线的定义和性质，等腰直角三角形的判定和性质，正确的作出辅助线是解题的关键．
25．（12分）问题背景：
如图1：在四边形ABCD中，AB＝AD，∠BAD＝120°，F分别是BC，CD上的点．且∠EAF＝60°．探究图中线段BE，FD之间的数量关系．
（1）小王同学探究此问题的方法是：延长FD到点G．使DG＝BE．连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，他的结论应是 EF＝BE+DF ；（并写出证明过程）
探索延伸：
（2）如图2，若在四边形ABCD中，AB＝AD，F分别是BC，CD上的点∠BAD，上述结论是否仍然成立
【答案】（1）EF＝BE+DF；证明过程见解答；
（2）成立，理由见解答．
【分析】（1）先利用“SAS”判断△ABE≌△ADG得到AE＝AG，∠BAE＝∠DAG，再证明∠EAF＝∠GAF，接着根据“SAS”判断△AEF≌△AGF，所以EF＝FG，从而得到EF＝BE+DF；
（2）结论仍然成立，证明方法与（1）相同．
【解答】解：（1）EF＝BE+DF．
证明如下：如图1，
在△ABE和△ADG中，
，
∴△ABE≌△ADG（SAS），
∴AE＝AG，∠BAE＝∠DAG，
∵∠EAF＝60°，∠BAD＝120°，
∴∠GAF＝∠DAG+∠DAF＝∠BAE+∠DAF＝∠EAF，
∴∠EAF＝∠GAF，
在△AEF和△GAF中，
，
∴△AEF≌△AGF（SAS），
∴EF＝FG，
∵FG＝DG+DF＝BE+DF，
∴EF＝BE+DF；
故答案为EF＝BE+DF；
（2）结论EF＝BE+DF仍然成立．
理由如下：延长FD到点G使DG＝BE，连接AG，
∵∠B+∠ADF＝180°，∠ADF+∠ADG＝180°，
∴∠B＝∠ADG，
在△ABE和△ADG中，
，
∴△ABE≌△ADG（SAS），
∴AE＝AG，∠BAE＝∠DAG，
∵∠EAF＝∠BAD，
∴∠GAF＝∠DAG+∠DAF＝∠BAE+∠DAF＝∠EAF，
∴∠EAF＝∠GAF，
在△AEF和△GAF中，
，
∴△AEF≌△AGF（SAS），
∴EF＝FG，
∵FG＝DG+DF＝BE+DF，
∴EF＝BE+DF．
【点评】本题考查了全等三角形的判定与性质：全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具．在判定三角形全等时，关键是选择恰当的判定条件．构建△ADG与△ABE是解决问题的关键．