初中数学冀教版八年级上册16.1 轴对称优秀一课一练

这是一份初中数学冀教版八年级上册16.1 轴对称优秀一课一练，共3页。试卷主要包含了下列说法中错误的是等内容，欢迎下载使用。


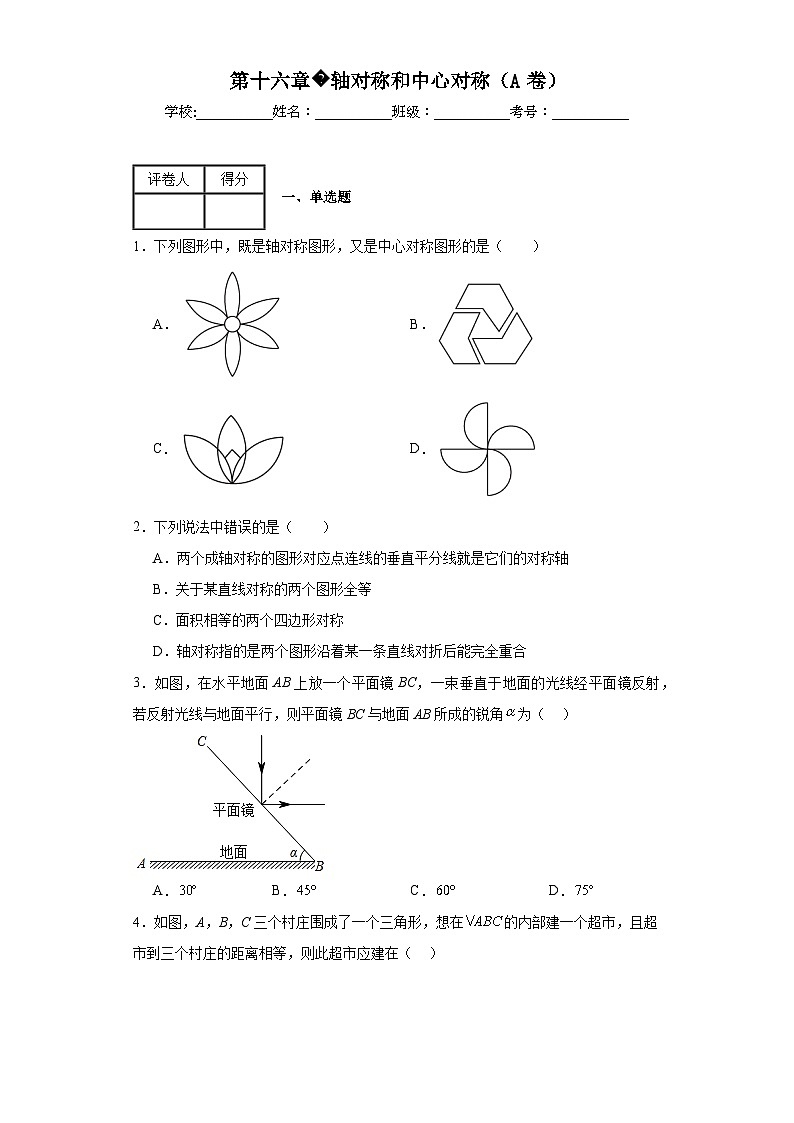
1．下列图形中，既是轴对称图形，又是中心对称图形的是（ ）
A．B．
C．D．
2．下列说法中错误的是（ ）
A．两个成轴对称的图形对应点连线的垂直平分线就是它们的对称轴
B．关于某直线对称的两个图形全等
C．面积相等的两个四边形对称
D．轴对称指的是两个图形沿着某一条直线对折后能完全重合
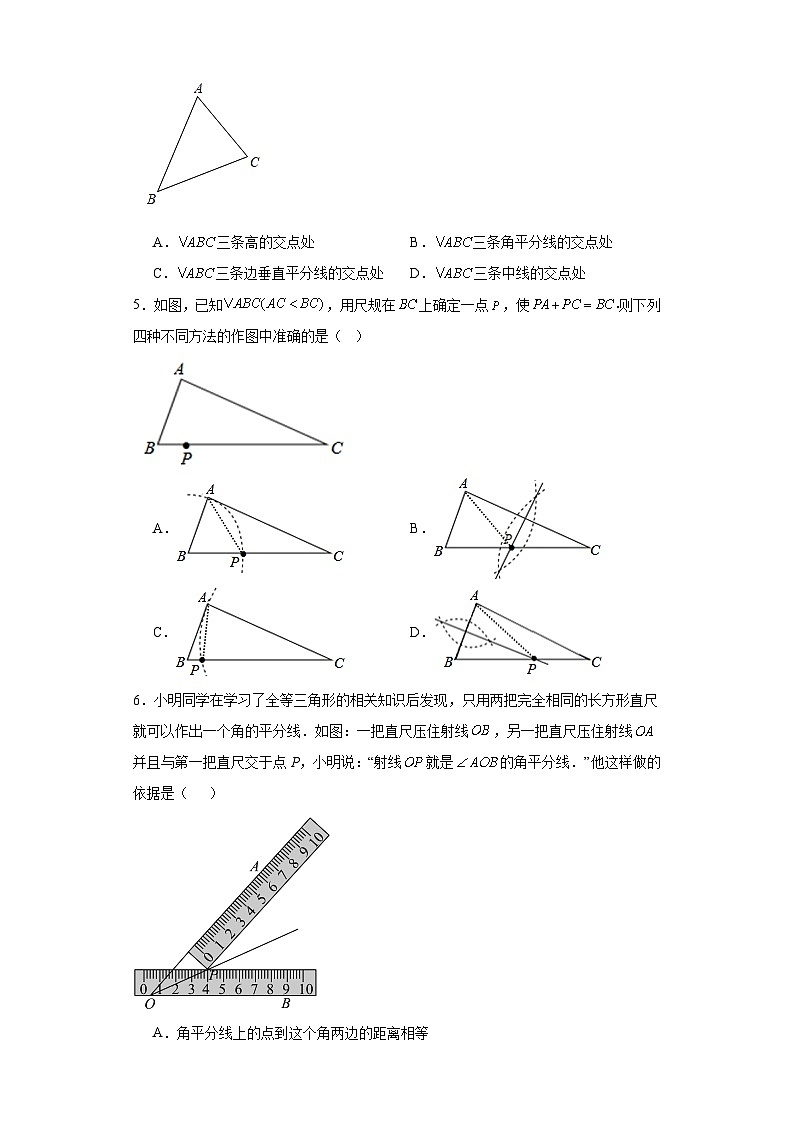
3．如图，在水平地面AB上放一个平面镜BC，一束垂直于地面的光线经平面镜反射，若反射光线与地面平行，则平面镜BC与地面AB所成的锐角为（ ）
A．B．C．D．
4．如图，A，B，C三个村庄围成了一个三角形，想在的内部建一个超市，且超市到三个村庄的距离相等，则此超市应建在（ ）
A．三条高的交点处B．三条角平分线的交点处
C．三条边垂直平分线的交点处D．三条中线的交点处
5．如图，已知，用尺规在上确定一点，使则下列四种不同方法的作图中准确的是（ ）
A．B．
C．D．
6．小明同学在学习了全等三角形的相关知识后发现，只用两把完全相同的长方形直尺就可以作出一个角的平分线．如图：一把直尺压住射线，另一把直尺压住射线并且与第一把直尺交于点P，小明说：“射线就是的角平分线．”他这样做的依据是（ ）
A．角平分线上的点到这个角两边的距离相等
B．角的内部到角的两边的距离相等的点在角的平分线上
C．三角形三条角平分线的交点到三条边的距离相等
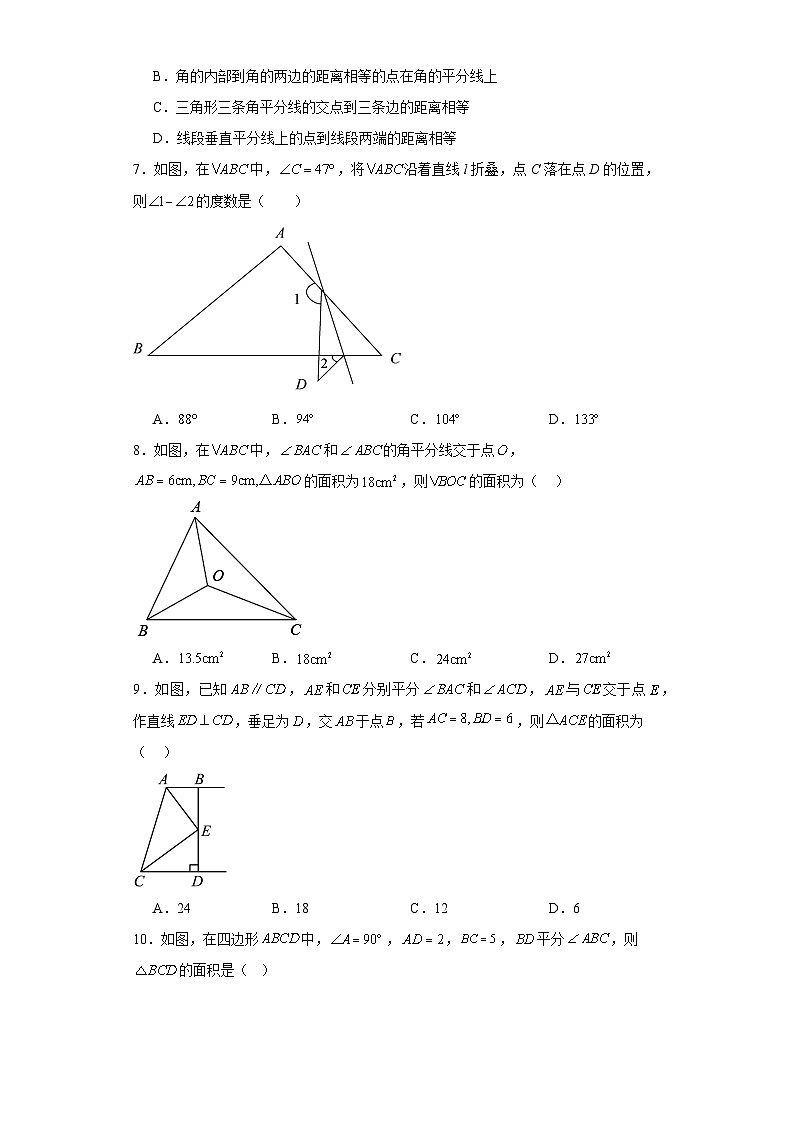
D．线段垂直平分线上的点到线段两端的距离相等
7．如图，在中，，将沿着直线l折叠，点C落在点D的位置，则的度数是（ ）
A．B．C．D．
8．如图，在中，和的角平分线交于点，的面积为，则的面积为（ ）
A．B．C．D．
9．如图，已知，和分别平分和，与交于点，作直线，垂足为，交于点，若，则的面积为（ ）
A．24B．18C．12D．6
10．如图，在四边形中，，，，平分，则的面积是（ ）
A．5B．6C．8D．10
11．如图，三圆同心于O，，于O，则图中阴影部分面积为 cm2．
12．已知点与点关于原点对称，则的值是 ．
13．如图，在中，，，，以点A为圆心，适当长为半径画弧，交于点M，交于点N，分别以点M，N为圆心，大于的长为半径画弧，两弧在的内部相交于点G，画射线，交于点D，点F在边上，且，连接，则的周长为 ．
14．如图，垂直平分于垂直平分于，若，则的周长为 ．
15．如图，和是由沿着、边翻折得到的，若，则的度数为 ．
16．如图，将沿折叠使得顶点C恰好落在边上的点M处，D在上，点P在线段上移动，若，，，则周长的最小值为 ．

17．在小正方形构成的网格中，每个小正方形的顶点叫做格点．
(1)的三个顶点都在格点上．
①在图1中，画出一个与成中心对称的格点三角形；
②在图2中，画出绕着点C按顺时针方向旋转90°后的三角形．
(2)如图3是由5个边长为1的小正方形拼成的图形，请用无刻度的直尺画经过点P的一条直线，使它平分该图形的面积，保留连线的痕迹，不要求说明理由．
18．如图，已知在△ABC中，∠BAC＝80°，∠ACB＝70°．
(1)尺规作图：按要求完成下列作图（不写作法，保留作图痕迹）：
①作∠BAC的角平分线AF，交BC于F；
②作线段AB的垂直平分线DE，分别交AB、BC于点D、点E；
(2)在（1）的条件下，连接AE，∠EAF=_____°．
19．如图，在中，的垂直平分线交于点E，交于点F，点D为的中点，连接，此时，．求证：．
20．图1是一个平分角的仪器，其中．
(1)如图2，将仪器放置在上，使点O与顶点A重合，D，E分别在边上，沿画一条射线，交于点P．是的平分线吗？请判断并说明理由．
(2)如图3，在（1）的条件下，过点P作上于点Q，若，的面积是60，求的长．
21．如图所示，已知是内的一点，点、分别是点关于、的对称点，与、分别相交于点、，已知．
(1)求的周长；
(2)连接、，判断的形状，并说明理由；
(3)若，求（用含的代数式表示）．
22．如图所示，在中，，是的平分线，交于，在上，．
证明：
(1)；
(2)．
23．综合与实践：折纸中的数学
知识背景
我们在七年级上册第四章《几何图形初步》中探究了简单图形折叠问题，并进行了简单的计算与推理．七年级下册第五章我们学习了平行线的性质与判定，今天我们继续探究：折纸中的数学﹣﹣长方形纸条的折叠与平行线．
知识初探
(1)如图1，长方形纸条ABGH中，，∠A＝∠B＝∠G＝∠H＝，将长方形纸条沿直线CD折上，点A落在A'处，点B落在B'处，B'C交AH于点E，若∠ECG＝，则∠CDE＝ ；
类比再探
(2)如图2，在图1的基础上将∠HEC对折，点H落在直线EC上的H'处，点G落在G'处得到折痕EF，则折痕EF与CD有怎样的位置关系？说明理由；
(3)如图3，在图2的基础上，过点G'作BG的平行线MN，请你猜想∠ECF和∠H'G'M的数量关系，并说明理由．
评卷人
得分
一、单选题
评卷人
得分
二、填空题
评卷人
得分
三、作图题
评卷人
得分
四、解答题
评卷人
得分
五、计算题
参考答案：
1．A
【分析】根据中心对称和轴对称的定义即可得出答案．
【详解】A．是轴对称图形，是中心对称图形，故本选项符合题意；
B．不是轴对称图形，不是中心对称图形，故本选项不符合题意；
C．是轴对称图形，不是中心对称图形，故本选项不符合题意；
D．不是轴对称图形，是中心对称图形，故本选项不符合题意．
故选：A．
【点睛】本题考查了中心对称图形与轴对称图形的概念，解题的关键是掌握寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后与原图重合．
2．C
【分析】根据轴对称的概念：如果有一个图形沿着某一条直线折叠能够与另一个图形重合，那么就说这两个图形关于这条直线对称，这条直线叫做对称轴，且是任何一对对应点所连线段的垂直平分线，据此进行分析即可．
【详解】解：A、两个成轴对称的图形对应点连线的垂直平分线就是它们的对称轴，选项正确，不符合题意；
B、关于某直线对称的两个图形全等，选项正确，不符合题意；
C、面积相等的两个四边形不一定能完全重合，不一定对称，选项错误，符合题意；
D、轴对称指的是两个图形沿着某一条直线对折后能完全重合，选项正确，不符合题意．
故选：C
【点睛】本题考查了轴对称的概念和性质，熟练掌握其概念是解题的关键．
3．B
【分析】利用平行线的性质和光的反射原理计算．
【详解】解：入射光线垂直于水平光线，
它们的夹角为90°，虚线为法线，为入射角，
两水平线平行
故选：B．
【点睛】本题考查平行线的性质、光的反射原理、入射角等于反射角等知识，是基础考点，掌握相关知识是解题关键．
4．C
【分析】要求超市到三个村庄的距离相等，首先思考到A村庄、B村庄距离相等，根据线段垂直平分线的判定定理知满足条件的点在线段的垂直平分线上，同理到B村庄、C村庄的距离相等的点在线段的垂直平分线上，于是到三个村庄的距离相等的点应是其交点，又因为三角形三边的垂直平分线相交于一点，所以答案可得．
【详解】解：根据线段垂直平分线的判定可知：和一条线段两个端点的距离相等的点在这条线段的垂直平分线上，
可知超市应建在三条边的垂直平分线的交点处．
故选：C．
【点睛】本题主要考查线段的垂直平分线的判定：和一条线段两个端点的距离相等的点在这条线段的垂直平分线上；此题是一道实际应用题，做题时，可分别考虑，先满足到两个村庄的距离相等，再满足到另两个村庄的距离相等，交点即可得到．
5．D
【分析】利用线段垂直平分线的性质以及圆的性质分别分得出即可．
【详解】解：A、由作法可知，则无法得出，故不能得出，故不符合题意；
B、由作法可知，则无法得出，故不能得出，故不符合题意；
C、由作法可知，则无法得出，故不能得出，故不符合题意；
D、由作法可知 ，故能得出，故符合题意；
故选：D．
【点睛】此题主要考查了复杂作图，熟练掌握线段垂直平分线的性质是解题关键．
6．B
【分析】如图，过点作于E点，于F点，则，然后根据角平分线的性质定理的逆定理可判断平分．
【详解】解：如图，过点作于E点，于F点，
∵两把长方形直尺完全相同，
∴，
∴平分（角的内部到角的两边的距离相等的点在这个角的平分线上），
故选：B．
【点睛】本题考查了作图−基本作图：熟练掌握5种基本作图是解决问题的关键．也考查了角平分线的性质和线段垂直平分线的性质．
7．B
【分析】由折叠的性质得到，再利用外角性质即可求出所求角的度数．
【详解】解：由折叠的性质得：，
根据外角性质，可得，，
则，
则．
故选：B．
【点睛】本题主要考查了翻折变换（折叠问题）和外角性质的知识，熟练掌握折叠的性质是解题的关键．
8．D
【分析】过点作于点，于点，根据角平分线的性质得出，根据三角形面积得出，代入数据即可求解．
【详解】解：过点作于点，于点，如图，
∵平分，
∴，
∴，
∴．
故选：D．
【点睛】本题考查了角平分线的性质，掌握角平分线的性质是解题的关键．
9．C
【分析】过点作于点，根据角平分线的性质得出，从而求出的长度，然后根据三角形面积计算公式计算即可．
【详解】解：过点作于点，
∵，，
∴，
∵和分别平分和，
∴，
∴点是的中点，
∵，
∴，
∴，
故选：C．
【点睛】本题考查了角平分线的性质，熟知角平分线上的任意一点到角两边的距离相等是解本题的关键．
10．A
【分析】过点作于，根据角平分线的性质得到，根据三角形面积公式计算即可．
【详解】解：过点作于，如图，
平分，，，
，
的面积．
故选：A．
【点睛】本题考查了角平分线的性质：角平分线上的点到角的两边的距离相等．
11．
【分析】根据圆的对称性可得图中阴影部分的面积正好是圆的面积的，进而就可以求得．
【详解】解：阴影部分的面积，
故答案为：．
【点睛】本题考查了圆是轴对称图形，两条相互垂直的直径是圆的对称轴，解题的关键是注意把不同的部分转移到一个图形中作答．
12．1
【分析】根据关于原点的对称点，横纵坐标都变成相反数，可得a、b的值，再代入所求式子计算即可．
【详解】解：∵与点关于原点对称，
∴，
，
故答案是：1．
【点睛】本题考查了关于原点对称的点的坐标．熟练掌握关于原点对称的点的坐标规律：横纵坐标都变成相反数，是解题的关键．
13．10
【分析】直接利用基本作图方法结合全等三角形的判定与性质进而得出，即可得出答案．
【详解】解：∵，，，
，
由作图方法可得：平分，
，
在和中
，
，
，
的周长为：．
故答案为：．
【点睛】此题主要考查了基本作图以及全等三角形的判定与性质，正确理解基本作图方法是解题关键．
14．22
【分析】利用线段的垂直平分线的性质解决问题即可．
【详解】解：∵垂直平分，
∴，
∵垂直平分，
∴，
∴，
∴的周长，
故答案为：22．
【点睛】本题考查线段的垂直平分线的性质，解题的关键是熟练掌握基本知识，属于中考常考题型．
15．/80度
【分析】由题意设，利用三角形的内角和定理可求解的值，即可求解，再由折叠的性质“折叠前后两图形全等，即对应角相等，对应线段相等”可求得的度数，根据三角形外角的性质可求解即可．
【详解】解：∵，
∴设，
则，
解得，
∴，
由折叠可知，
∴，
∴．
故答案为：．
【点睛】本题主要考查了折叠的性质、三角形内角和定理、三角形外角的性质等知识，熟练掌握相关知识是解题关键．
16．19
【分析】首先明确要使得周长最小，即使得最小，再根据翻折的性质可知，从而可得满足最小即可，根据两点之间线段最短确定即为最小值，从而求解即可．
【详解】解：由翻折的性质可知，，，
∴M点为上一个固定点，则长度固定，
∵，
∴要使得周长最小，即使得最小，
∵，
∴满足最小即可，
显然，当P、B、C三点共线时，满足最小，如图所示，
此时，P点与D点重合，，
∴周长最小值即为，
根据折叠可知，，
∵，
∴，
∵，
∴周长最小值即为，
故答案为：19．
【点睛】本题考查翻折的性质，以及最短路径问题等，掌握翻折的基本性质，理解并熟练运用两点之间线段最短是解题关键．
17．(1)①见解析；②见解析
(2)见解析
【分析】（1）①以点C为对称中心，画出图形即可；②根据旋转的性质，即可画出；
（2）根据中心对称图形的性质即可解决问题．
【详解】（1）①如图1，即为所求；
②如图2，即为所求；
（2）如图3，即为画出直线．
【点睛】本题主要考查了作图﹣旋转变换，中心对称图形的性质等知识，熟练掌握中心对称图形的性质是解题的关键．
18．(1)①见解析；②见解析；
(2)10．
【分析】（1）①根据角平分线的作法即可作的角平分线，交于F；
②根据线段垂直平分线的作法即可作线段的垂直平分线，分别交、于点D、点E；
（2）首先根据三角形内角和定理可得，然后根据线段垂直平分线的性质和角平分线的定义即可求出的度数．
【详解】（1）①如图，的角平分线即为所求；
②如图，线段的垂直平分线即为所求；
（2）∵，．
∴，
∵是的垂直平分线，
∴，
∴，
∵平分，
∴，
∴．
故答案为：10．
【点睛】本题考查了作图﹣复杂作图，线段垂直平分线的性质，解决本题的关键是掌握基本作图方法．
19．见解析
【分析】连接，根据三角形内角和定理得到，根据线段垂直平分线的性质得到，，等量代换证明结论．
【详解】证明：连接，
∵，，
∴，
∴，
∵点D为的中点，
∴，
∴AD是线段CE的垂直平分线，
∴，
∵EF垂直平分，
∴，
∴．
【点睛】本题考查的是线段垂直平分线的性质，掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键．
20．(1)是的平分线，理由见解析
(2)
【分析】（1）利用三条对应边相等证明来得到即可．
（2）利用角平分线上的点到角两边的距离相等得到的高，再运用割补法及面积计算公式解题即可．
【详解】（1）解：是的平分线
理由如下：在和中，，
∴
∴，
∴平分．
（2）解： ∵平分，，
∴的高等于，
∵．
∴，
∵
∴．
【点睛】本题主要考查三角形全等的判定方法及角平分线的性质，能够熟练运用角平分线的性质得到高的长度是解题关键．
21．(1)的周长为；
(2)是等腰三角形，理由见解析
(3)．
【分析】（1）根据轴对称的性质，可得，根据三角形的周长公式，可得答案；
（2）根据轴对称的性质，可得，根据等腰三角形的判定，可得答案；
（3）根据轴对称的性质，可得，根据角的和差，可得答案．
【详解】（1）解：由点M、N分别是O点关于、的对称点，得
．
由三角形的周长，得
；
（2）解：是等腰三角形，
理由：如图：
，
由点M、N分别是O点关于、的对称点，得
，
∴，
∴是等腰三角形；
（3）解：由点M、N分别是O点关于、的对称点，得
．
由角的和差，得
，
∴，
∴．
【点睛】本题考查了轴对称，利用对称轴上的点到线段两端点的距离相等是解题关键．
22．(1)见解析
(2)见解析
【分析】（1）证明即可；
（2）由，结合条件可知且，代入可证得结论．
【详解】（1）∵是的平分线，，，
∴，，
∴在和中，
∴，
∴；
（2）∵是的平分线，，，
∴，
由已知有：，，
∴ ，
在和中，
∴，
∴，
由（1）知，
∴．
【点睛】此题考查了三角形全等的判定方法，角平分线的性质定理，解题的关键是熟练掌握三角形全等的判定方法．判定三角形全等的方法有：，，，，(直角三角形)．
23．(1)
(2)，理由见解析
(3)，理由见解析
【分析】（1）先根据折叠的性质可得，再根据平角的定义可得，然后根据平行线的性质即可得；
（2）先根据折叠的性质可得，，再根据平行线的性质可得，从而可得，然后根据平行线的判定即可得出结论；
（3）过点作于，先根据平行线的性质可得，再根据平行公理推论可得，根据平行线的性质可得，然后根据折叠的性质可得，从而可得，最后根据等量代换即可得出结论．
【详解】（1）解：由折叠的性质得：，
，，
，
，
，
故答案为：．
（2）解：，理由如下：
由折叠的性质得：，，
，
，
，
．
（3）解：，理由如下：
如图，过点作于，
，
又，
，
，
由折叠的性质得：，
，
．
【点睛】本题考查了折叠的性质、平行线的判定与性质、平行公理推论等知识点，熟练掌握平行线的性质和折叠的性质是解题关键．