初中数学北师大版八年级上册4 一次函数的应用第3课时教案及反思

这是一份初中数学北师大版八年级上册4 一次函数的应用第3课时教案及反思，共18页。教案主要包含了教学重点，教学难点等内容，欢迎下载使用。
第 3 课时
教材分析
本节课是北师大版义务教育教科书八年级上册第四章第四节的第3课时，主要是利用两个一次函数的图象解决一些生活中的实际问题.和前一课时一样，教科书注重从函数图象中获取信息从而解决具体问题，关注数形结合思想的揭示，关注形象思维能力的发展，同时，这为今后学习用图象法解二元一次方程组打下基础.
教学目标
进一步训练学生的识图能力，能通过函数图象获取信息，解决简单的实际问题；在解决问题过程中，初步体会方程与函数的关系，建立各种知识的联系.
在函数图象信息获取过程中，进一步培养学生的数形结合意识，发展形象思维；在解决实际问题过程中，进一步发展学生的分析问题、解决问题的能力和数学应用意识.
在现实问题的解决中，使学生初步认识数学与人类生活的密切联系，从而培养学生学习数学的兴趣.
教学重难点
【教学重点】
能通过函数图象获取信息，解决简单的实际问题.
【教学难点】
真正读懂函数图象的实际意义.
课前准备

学生每人准备好草稿纸、铅笔、直尺；
教师准备课件，图片.
教学过程
一、创设情境，引入新知
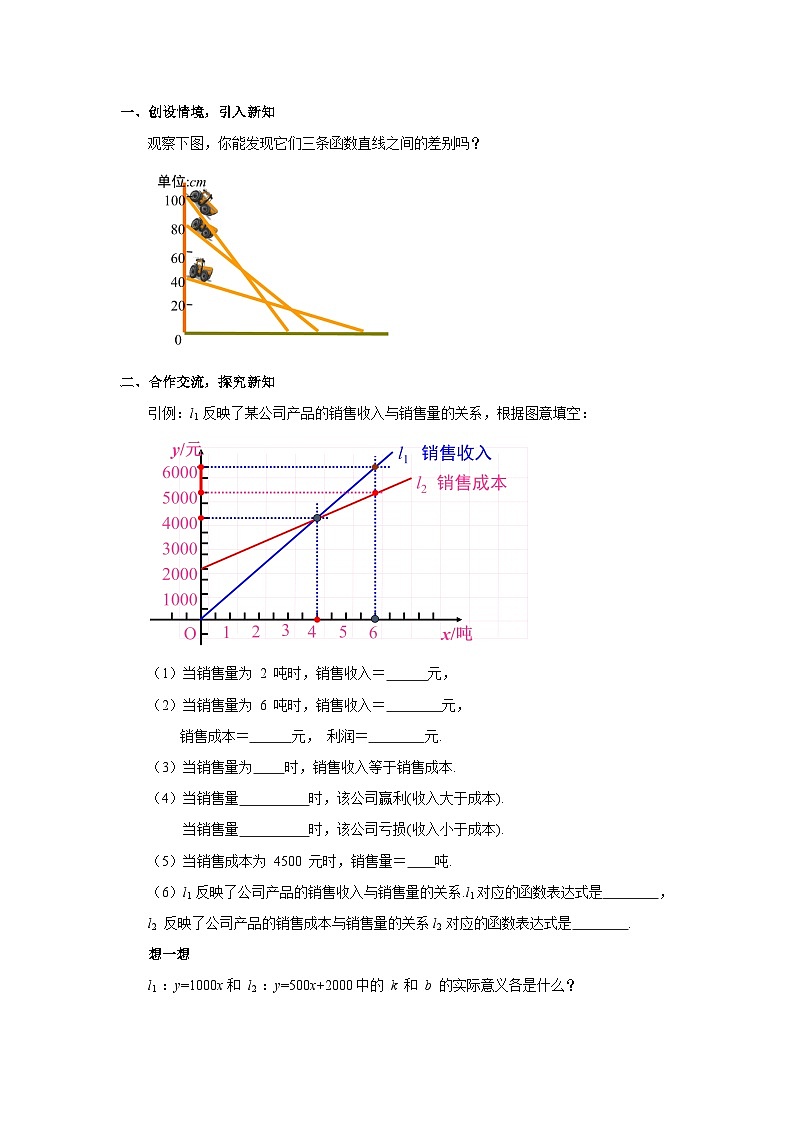
观察下图，你能发现它们三条函数直线之间的差别吗？
二、合作交流，探究新知
引例：l1 反映了某公司产品的销售收入与销售量的关系，根据图意填空：
（1）当销售量为 2 吨时，销售收入＝ 元，
（2）当销售量为 6 吨时，销售收入＝ 元，
销售成本＝ 元， 利润＝ 元.
（3）当销售量为 时，销售收入等于销售成本.
（4）当销售量 时，该公司赢利(收入大于成本).
当销售量 时，该公司亏损(收入小于成本).
（5）当销售成本为 4500 元时，销售量＝ 吨.
（6）l1 反映了公司产品的销售收入与销售量的关系.l1对应的函数表达式是 ，
l2 反映了公司产品的销售成本与销售量的关系l2 对应的函数表达式是 .
想一想
l1 ：y=1000x和 l2 ：y=500x+2000中的 k 和 b 的实际意义各是什么？
三、运用新知
海
岸
公
海
A
B
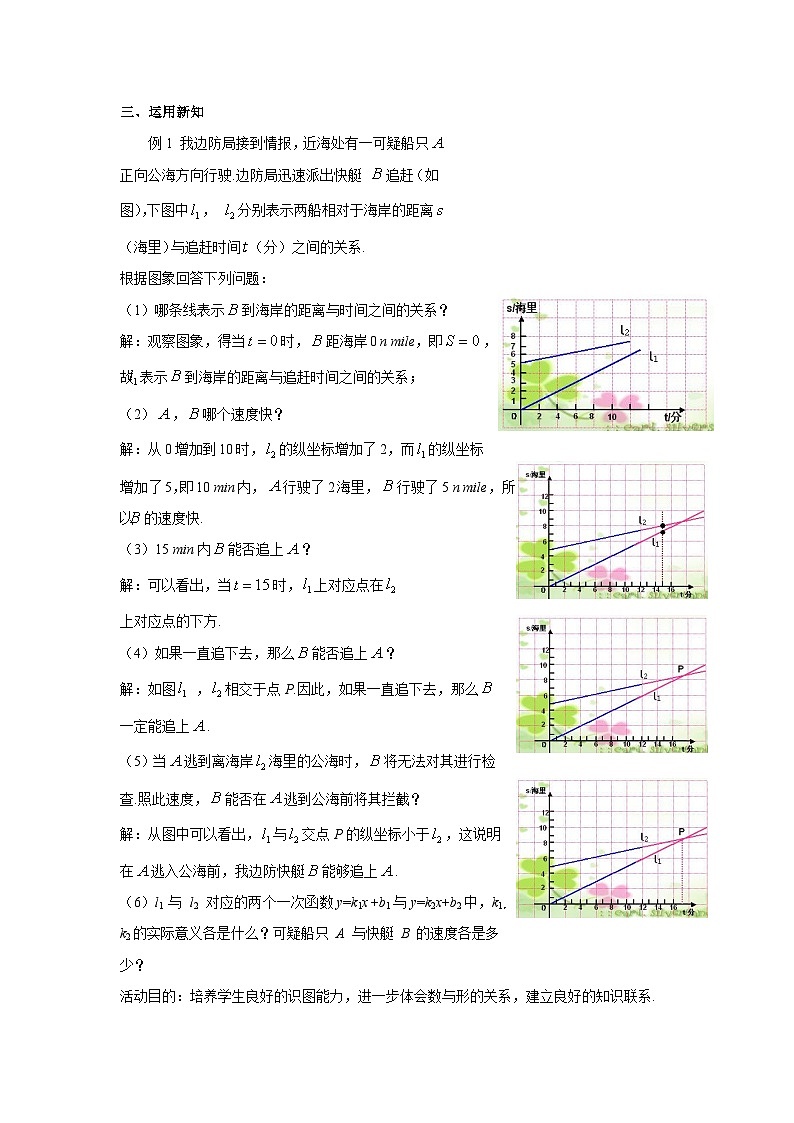
例1 我边防局接到情报，近海处有一可疑船只正向公海方向行驶.边防局迅速派出快艇 追赶（如图），下图中， 分别表示两船相对于海岸的距离（海里）与追赶时间（分）之间的关系.
根据图象回答下列问题：
（1）哪条线表示到海岸的距离与时间之间的关系？
解：观察图象，得当时，距海岸0 n mile，即，故表示到海岸的距离与追赶时间之间的关系；
（2），哪个速度快？
解：从0增加到10时，的纵坐标增加了2，而的纵坐标增加了5，即10 min内，行驶了2海里，行驶了5 n mile，所以的速度快.
（3）15 min内能否追上？
解：可以看出，当时，上对应点在
上对应点的下方.
（4）如果一直追下去，那么能否追上？
解：如图 ，相交于点P.因此，如果一直追下去，那么一定能追上.
（5）当逃到离海岸海里的公海时，将无法对其进行检查.照此速度，能否在逃到公海前将其拦截？
解：从图中可以看出，与交点P的纵坐标小于，这说明在逃入公海前，我边防快艇能够追上.
（6）l1 与 l2 对应的两个一次函数y=k1x +b1与y=k2x+b2中，k1，k2的实际意义各是什么？可疑船只 A 与快艇 B 的速度各是多少？
活动目的：培养学生良好的识图能力，进一步体会数与形的关系，建立良好的知识联系.
说明：学生在教师的引导下，逐步形成了良好的识图能力.
例2 已知一次函数y＝32x＋a和y＝-12x＋b的图象都经过点 A(－4，0)，且与 y 轴分别交于 B、C 两点，求△ABC 的面积
四、巩固新知
1. 如图，射线OA、BA分别表示甲、乙两人骑自行车运动过程的一次函数的图象，图中 s、t 分别表示行驶距离和时间，则这两人骑自行车的速度相差 km/h.
2. 一次越野跑中，当小明跑了1600米时，小刚跑了1400米，小明、小刚所跑的路程 y（米）与时间 t（秒）之间的函数关系如图，则这次越野跑的全程为 米.
3. 小亮和小明周六到距学校 24 km的滨湖湿地公园春游，小亮8：00从学校出发，骑自行车去湿地公园，小明 8：30 从学校出发，乘车沿相同路线去滨湖湿地公园，在同一直角坐标系中，小亮和小明的行进路程 S（km）与时间 t（时）的函数图象如图所示.根据图象得到结论，其中错误的是（ ）.
A．小亮骑自行车的平均速度是12km/h
B．小明比小亮提前0.5小时到达滨湖湿地公园
C．小明在距学校12km处追上小亮
D．9：30小明与小亮相距4km
4. 在一次蜡烛燃烧试验中，甲、乙两根蜡烛燃烧时剩余部分的高度y（厘米）与燃烧时间x（时）之间的关系如图所示，请根据图象所提供的信息解答下列问题：
（1）甲、乙两根蜡烛燃烧前的高度分别是 ，从点燃到燃尽所用的时间分别是 、
（2）分别求甲、乙两根蜡烛燃烧时y与x之间的函数关系式；
（3）燃烧多长时间时，甲、乙两根蜡烛的高度相等（不考虑都燃尽时的情况）？
在什么时间段内，甲蜡烛比乙蜡烛高？
在什么时间段内，甲蜡烛比乙蜡烛低？
五、归纳小结
内容：本节课我们学习了一次函数图象的应用，在运用一次函数解决实际问题时，可以直接从函数图象上获取信息解决问题，当然也可以设法得出各自对应的函数关系式，然后借助关系式完全通过计算解决问题.通过列出关系式解决问题时，一般首先判断关系式的特征，如两个变量之间是不是一次函数关系？当确定是一次函数关系时，可求出函数解析式，并运用一次函数的图象和性质进一步求得我们所需要的结果.
意图：引导学生自己小结运用一次函数解决实际问题的主要方法.
说明：让学生畅所欲言，相互进行补充，尽量用自己的语言进行归纳总结.
教学反思
略.