






数学4.1 角的概念的推广课前预习课件ppt
展开在义务教育阶段我们学习过,角是有公共端点的两条射线构成的图形.
4.1 角的概念的推广
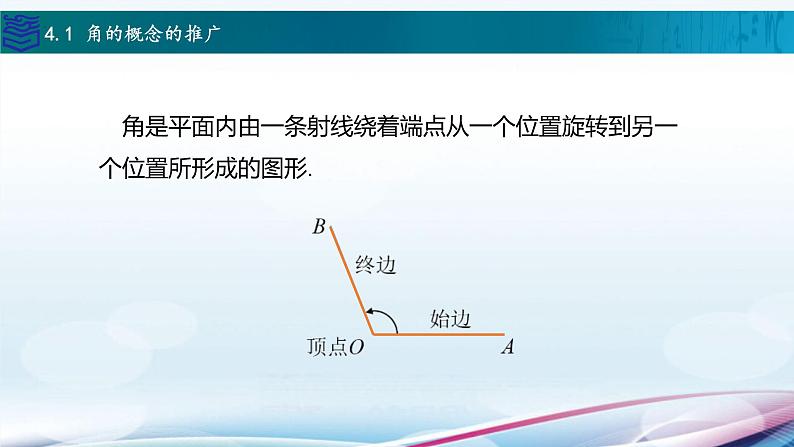
角是平面内由一条射线绕着端点从一个位置旋转到另一个位置所形成的图形.
已经学习过的角包括锐角、直角、钝角、平角 、周角等,它们都在0° ~ 360°范围内.
公园里的摩天轮,选定一个机械臂的起始位置作为始边,如果机械臂从这个起始位置旋转一周,就说它转过了360°,那么当它转过一周半或者转过两周时,它转过了多少度呢?
如果时钟快了2h,应该如何校准?校准过程中分针相对起始位置转过了多少度?如果时钟慢了2h呢?
摩天轮的机械臂从起始位置, 旋转了一周, 则说它转过了360° ,旋转一周半,则说它转过了540° , 旋转了两周,则说它转过了720°.
如果时钟快了2h,则需要将分针相对于起始位置逆时针旋转720°,如果时钟慢了2h,则需要将分针相对于起始位置顺时针旋转720°.
由于旋转的方向不同,其效果也不同.因此,关于角,不仅要知道旋转的度数,还要考虑旋转的方向.
规定:一条射线绕其端点按逆时针方向旋转形成的角称为正角,如图(1)所示;按顺时针方向旋转形成的角称为负角,如图(2)所示.
如果一条射线没有做任何旋转,也认为形成了一个角,这个角称为零角.
分针按逆时针方向旋转2周形成的角,记作720°,如图(1)所示;分针按顺时针方向旋转2周形成的角,记作-720°,如图(2)所示.
(1) (2)
通常使用角的顶点或顶点与始边、终边上的字母来表示角.例如,下图中的角,可以记作“∠AOB”或“∠O”.
也经常使用小写的希腊字母 α,β, γ,…来表示角,记作“角α”.在不引起混淆的情况下,可以简记成“α”. 例如,α=420°, β= −135°.
设角α与角β是两个任意角,如何理解角-α 、角α + β和角α-β ?
为了方便,通常在平面直角坐标系中讨论角. 将角的顶点与原点重合,角的始边与x轴的非负半轴重合,此时角的终边在第几象限,就称这个角为第几象限角.
角∠AOB”是第一象限角
角∠AOB”是第二象限角
角∠AOB”是第三象限角
角∠AOB”是第四象限角
如果角的终边在坐标轴上, 就认为这个角不属于任何一个象限,称为界限角.如, 0°,90°,180°,360°,−90°角都是界限角.
(1) 490°角是射线绕着原点逆时针旋转490°形成的, 终边落在第二象限, 所以490°为第二象限角;
例1 在平面直角坐标系中,叙述下列各角的形成过程,并指出它们是第几象限角. (1) 490° ;(2)−650° .
解 将角的顶点与坐标原点重合,角的始边与x轴的非负半轴重合.
(2) −650°角是射线绕着原点顺时针旋转650°形成的, 终边落在第一象限, 所以−650°为第一象限角.
例2 求时钟从8点到9点15分, 如图所示, 分针和时针旋转所成的角.
解 时钟8点到9点15分, 分针顺时针旋转450° , 因此, 分针旋转形成的角为−450°;而时针顺时针旋转了37.5° , 因此, 时针旋转形成的角为−37.5°.
1.填空题:(1) −15°是第_________象限角;(2) 795°是第_________象限角;(3) 163°是第_________象限角;(4) −458°是第________象限角.
2.判断题(正确的打“√”,错误的打“×”):(1)第四象限角一定是负角; ( )(2) 第二象限角一定是正角; ( )(3)小于90°的角一定是锐角; ( )(4)第一象限角一定是锐角; ( )(5)钝角一定是第二象限角; ( )(6)第二象限角一定是钝角. ( )
3.在平面直角坐标系中, 分别作出下列各角, 并指出它们是第几象限角:(1) 460° ; (2) 945°; (3) −200° ; (4) −700° .
4.1.2 终边相同的角
如图, 30°, −330°, 390°角之间有什么关系呢?
不难发现, 在平面直角坐标系中,这三个角的终边相同, 并且都可以表示成30°与k个(k ∈Z) 360°的和.如:
30° = 30°+0×360° ; −330° = 30°+ (−1)×360° ; 390° = 30°+1× 360° .
从上述角的形成过程可以看出,与30°终边相同的角有无数多个,它们与30°角均相差360°的整数倍. 因此与30°终边相同的所有角可以表示为 β= 30° +k360°,k∈Z.
一般地,与角α终边相同的所有角构成的集合为 S={β|β=α+ k360°,k∈Z},即,所有与角α终边相同的角都可以表示成角α与360°的整数倍的和.
例3 写出与−950°角终边相同的所有角构成的集合,并找出0°~360°范围内与其终边相同的角.
解 与−950°角终边相同的所有角构成的集合为 S={β|β=−950°+ k 360°,k∈Z }. 当k=3时, β=−950°+3 360° = 130°,故在0°~360°范围内, 与−950°角终边相同的角是130°角.
因为−950°与130°终边相同,集合 S={β|β=−950°+k360°,k∈Z}也可写成 S={β|β=130°+k360°,kZ}.
例4 写出终边在射线y=x(x≥0)上的角组成的集合.
解 在0°~360°范围, 终边在射线y=x(x≥0)上的角为45°角,
因此终边在射线 y=x(x≥0)上的角组成的集合为 S={β|β=450°+k·360° , k∈Z}.
例5 写出终边在y轴上的角组成的集合.
解 在0°~360°范围, 终边在y轴上的角有90°角和270°角.
所有与90°角和270°角终边相同的角组成的集合分别为 S1={β|β=90°+ k·360°, k∈Z} 和 S2={β|β=270°+ k·360°, k∈Z}.所以,S=S1∪S2 ={β|β= 90°+ k·360°, k∈Z}∪{β|β=270°+ k·360°, k∈Z} = {β|β= 90°+ 2k·180°, ∈Z}∪{β|β=90°+(2k+1) ·180°, k∈Z} = {β|β=90°+n·180°, n∈Z}.
若角α是第一象限角,试写出角 α 的集合.
1.已知角α是第一象限角,则角−α的终边在第_______象限.2 .与1560°角终边相同的角的集合中,最小的正角是_____.
3. 写出与下列角终边相同的所有角组成的集合,并在0°~360°范围内找出与其终边相同的角. (1) 420°; (2) −510°; (3) −73°; (4) 855°.
4. 写出终边在x轴上的角组成的集合.
1.书面作业:完成课后习题和学习与训练;2.查漏补缺:根据个人情况对课题学习复习与回顾;3.拓展作业:阅读教材扩展延伸内容.
高教版(中职)基础模块上册(2021)4.1.1 任意角图文ppt课件: 这是一份高教版(中职)基础模块上册(2021)4.1.1 任意角图文ppt课件,文件包含41角的概念的推广课件pptx、41角的概念的推广教案pdf、41角的概念的推广docx等3份课件配套教学资源,其中PPT共45页, 欢迎下载使用。
中职数学高教版(2021)基础模块上册4.1 角的概念的推广教学演示课件ppt: 这是一份中职数学高教版(2021)基础模块上册4.1 角的概念的推广教学演示课件ppt,共15页。PPT课件主要包含了初中角的定义,高中角的定义,“旋转”形成角,角α是第一象限角,角β是第三象限角等内容,欢迎下载使用。
中职数学高教版(2021)基础模块上册4.1 角的概念的推广说课ppt课件: 这是一份中职数学高教版(2021)基础模块上册4.1 角的概念的推广说课ppt课件,共15页。PPT课件主要包含了任意角,角的分类,角的定义,“旋转”形成角,终边相同的角,-32°,-392°,重点知识标红,3象限角的表示等内容,欢迎下载使用。












