浙江省杭州市江干区采荷中学2022-—2023学年上学期七年级期中数学试卷

这是一份浙江省杭州市江干区采荷中学2022-—2023学年上学期七年级期中数学试卷，共10页。试卷主要包含了选择题，填空题，简答题等内容，欢迎下载使用。
1．（3分）从百年前的“奥运三问”到今天的“双奥之城”，2022年中国与奥运再次牵手，2022年注定是不平凡的一年，数字2022的相反数是（ ）
A．2022B．﹣2022C．﹣D．
2．（3分）2022年10月1日，杭州西湖游客167500人，将167500用科学记数法表示法为（ ）
A．16.75×104B．1.675×105
C．1.675×104D．0.1675×106
3．（3分）下面各组式子中，属于同类项的是（ ）
A．2a和a2B．﹣2.5和2
C．﹣2x和﹣xyD．6xy2和5x2y
4．（3分）下列说法正确的是有（ ）
A．﹣36的平方根是﹣6B．25的平方根是5
C．平方根等于0的数是0D．64的立方根是8
5．（3分）下列去括号正确的是（ ）
A．a2﹣（2a﹣b2）＝a2﹣2a﹣b2
B．﹣（2x﹣y）﹣（﹣x2+y2）＝﹣2x﹣y+x2﹣y2
C．2x2﹣3（x﹣5）＝2x2﹣3x+5
D．﹣a3﹣[﹣4a2+（1﹣3a）]＝﹣a3+4a2﹣1+3a
6．（3分）多项式7x2﹣4x+23的项数及次数是（ ）
A．3，3B．2，3C．3，2D．2，2
7．（3分）在式子“﹣23〇（﹣1）2中的“〇”内填入下列运算符号，计算后结果最大的是（ ）
A．+B．﹣C．×D．÷
8．（3分）若|x|＝3，|y|＝6，且x＞y，则x﹣y的值是（ ）
A．﹣3和﹣9B．3和﹣6C．﹣3和9D．3和9
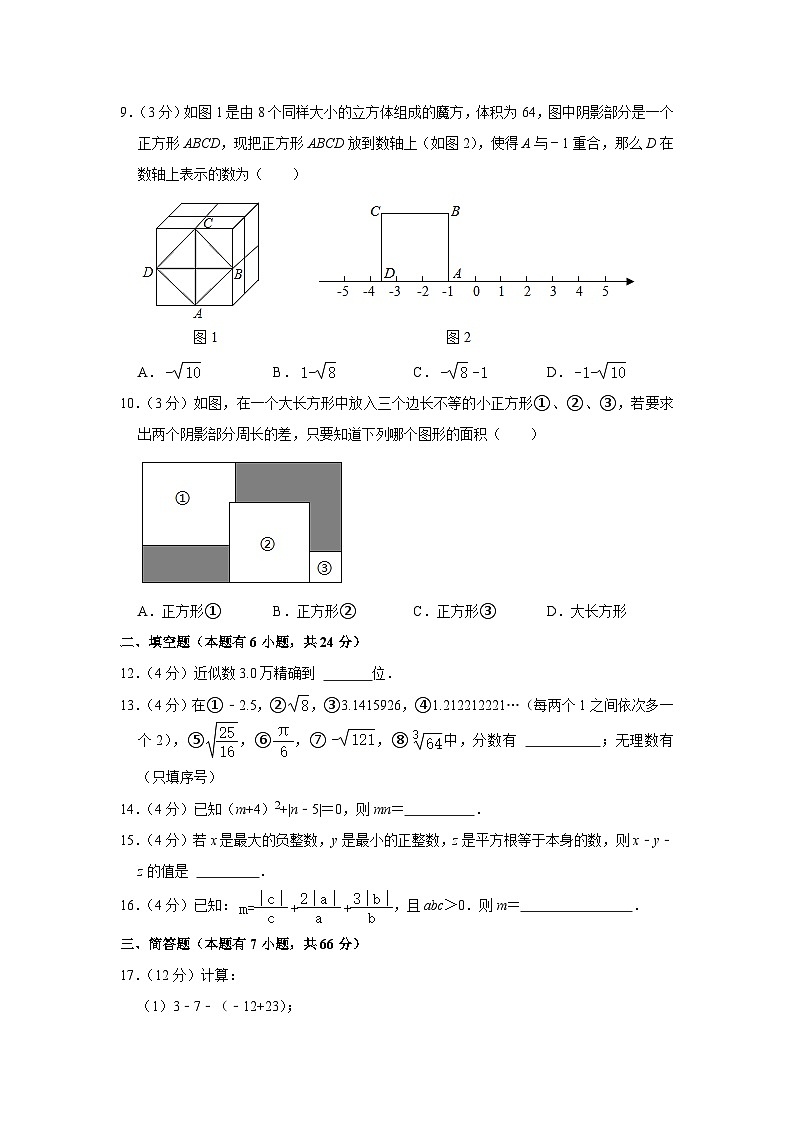
9．（3分）如图1是由8个同样大小的立方体组成的魔方，体积为64，图中阴影部分是一个正方形ABCD，现把正方形ABCD放到数轴上（如图2），使得A与﹣1重合，那么D在数轴上表示的数为（ ）
A．B．C．D．
10．（3分）如图，在一个大长方形中放入三个边长不等的小正方形①、②、③，若要求出两个阴影部分周长的差，只要知道下列哪个图形的面积（ ）
A．正方形①B．正方形②C．正方形③D．大长方形
二、填空题（本题有6小题，共24分）
12．（4分）近似数3.0万精确到 位．
13．（4分）在①﹣2.5，②，③3.1415926，④1.212212221…（每两个1之间依次多一个2），⑤，⑥，⑦，⑧中，分数有 ；无理数有 （只填序号）
14．（4分）已知（m+4）2+|n﹣5|＝0，则mn＝ ．
15．（4分）若x是最大的负整数，y是最小的正整数，z是平方根等于本身的数，则x﹣y﹣z的值是 ．
16．（4分）已知：，且abc＞0．则m＝ ．
三、简答题（本题有7小题，共66分）
17．（12分）计算：
（1）3﹣7﹣（﹣12+23）；
（2）（请用简便方法计算）；
（3）；
（4）．
18．（6分）（1）先化简，再求值：，其中a＝2，b＝﹣3．
（2）已知2x+y＝3，求代数式3（x﹣2y）+5（x+2y﹣1）﹣2的值．
19．（8分）义乌“8.2”疫情爆发后火速蔓延，根据疫情防控形势，东阳防控指挥部连续一段时间在全市范围开展全员核酸检测．为方便大家做核酸，各街道小区增设多个检测点．某便民检测点在8月8日当天共检测1800人次，在接下来的8月9日﹣8月15日的一周内，记录每天核酸检测人数相比前一天的增减情况如下表：（单位：人）
注：正号表示检测人数比前一天增加，负号表示检测人数比前一天减少．
（1）8月9日﹣8月15日的这一周内检测人数最多的是哪天？这天检测了多少人？
（2）8月9日﹣8月15日的这一周内检测人数最多的一天比人数最少的一天多检测多少人？
（3）在排队等候做核酸的过程中，小东观察到一个医务人员给一人做检测需要10秒，那么8月10日这天若只安排一个医务人员工作，从17：30开始到22：30能完成检测任务吗（不考虑其他准备时间）？
20．（8分）现定义新运算“⊙”，对于任意两个实数a，b，规定a⊙b＝ab﹣2a﹣2b．
（1）计算：3⊙5；
（2）若a⊙（3⊙k）的取值与a无关，求实数k．
21．（8分）已知，则的整数部分为1；而减去其整数部分的差就是的小数部分，则的小数部分为．根据以上的内容，解答下面的问题：
（1）填空：的整数部分是 ，的小数部分是 ．
（2）若，其中是m为整数，且0＜n＜1，求m﹣n的值．
22．（12分）若数轴上的点A、点B表示的数分别为a、b，则A、B两点之间的距离AB＝|a﹣b|，线段AB的中点表示的数为．如图：现数轴上有一点A表示的数为﹣10，点B表示的数为18，点P从点A出发，以每秒4个单位长度的速度沿数轴向右匀速运动，同时点Q从点B出发，以每秒3个单位长度的速度向左匀速运动，设运动时间为t秒．
（1）A、B两点之间的距离AB＝ ，线段AB的中点表示的数为 ．
（2）当t＝ 时，P、Q两点相遇，相遇点所表示的数为 ．
（3）求当t为何值时，．
23．（12分）某校需要订购中考专用的某款跳绳和排球，经调查发现，该款跳绳、排球各商家均标价为50元/条，40元/个，现有3家商店在做促销活动如下表：
（1）若在乙店购买10套，则总费用 元；在乙店购买40套，则总费用 元．
（2）若现在需要跳绳a条和排球a个，且仅在一家商店购买，请用含a的代数式分别表示甲、乙两店的总费用．
甲店总费用： ；
乙店总费用：当0＜a≤30时， ；当30＜a≤60时， ；当a＞60时， ．
（3）当需要购买60条跳绳和120个排球时，请你通过计算设计一种最省钱的购买方案，并求出总费用．
四、选择题（共1小题，每小题3分，满分3分）
24．（3分）已知当x＝1时，3ax3+bx2﹣2cx+4＝8，且ax3+2bx2﹣cx﹣15＝﹣14，则当x＝﹣1时，5ax3﹣5bx2﹣4cx+2022＝（ ）
A．2016B．2017C．2018D．2020
五、填空题（共3小题，每小题3分，满分9分）
25．（3分）若a、b、c、d是互不相等的整数（a＜b＜c＜d），且abcd＝121，则ac+bd＝ ．
26．（3分）已知|2009﹣a|+＝a，则a﹣20092＝ ．
27．（3分）已知动点A从原点O出发沿数轴向左运动，同时动点B也从原点出发沿数轴向右运动，动点A的速度为每秒1个单位长度，动点B的速度为每秒2个单位长度，5秒后动点B调转方向向左运动，A、B两点的速度仍保持不变，则 秒后A、B、O三点中一点到另两个点的距离相等．
2022-2023学年浙江省杭州市江干区采荷中学七年级（上）期中数学试卷
（参考答案）
一、选择题（本题有10小题，共30分）
1．（3分）从百年前的“奥运三问”到今天的“双奥之城”，2022年中国与奥运再次牵手，2022年注定是不平凡的一年，数字2022的相反数是（ ）
A．2022B．﹣2022C．﹣D．
【解答】解：2022的相反数是﹣2022，
故选：B．
2．（3分）2022年10月1日，杭州西湖游客167500人，将167500用科学记数法表示法为（ ）
A．16.75×104B．1.675×105
C．1.675×104D．0.1675×106
【解答】解：167500＝1.675×105．
故选：B．
3．（3分）下面各组式子中，属于同类项的是（ ）
A．2a和a2B．﹣2.5和2
C．﹣2x和﹣xyD．6xy2和5x2y
【解答】解：A．2a和a2，所含字母相同，但相同字母的指数不相同，不是同类项，故本选项不合题意；
B．﹣2.5和2是同类项，故本选项符合题意；
C．﹣2x和﹣xy，所含字母不相同，不是同类项，故本选项不合题意；
D．6xy2和5x2y，所含字母相同，但相同字母的指数不相同，不是同类项，故本选项不合题意．
故选：B．
4．（3分）下列说法正确的是有（ ）
A．﹣36的平方根是﹣6B．25的平方根是5
C．平方根等于0的数是0D．64的立方根是8
【解答】解：A．﹣36没有平方根，故此选项错误，不符合题意；
B．25的平方根是±5，故此选项错误，不符合题意；
C．平方根等于0的数是0，故此选项正确，符合题意；
D．64的立方根是4，故此选项错误，不符合题意．
故选：C．
5．（3分）下列去括号正确的是（ ）
A．a2﹣（2a﹣b2）＝a2﹣2a﹣b2
B．﹣（2x﹣y）﹣（﹣x2+y2）＝﹣2x﹣y+x2﹣y2
C．2x2﹣3（x﹣5）＝2x2﹣3x+5
D．﹣a3﹣[﹣4a2+（1﹣3a）]＝﹣a3+4a2﹣1+3a
【解答】解：A、a2﹣（2a﹣b2）＝a2﹣2a+b2，故本选项错误，不符合题意；
B、﹣（2x﹣y）﹣（﹣x2+y2）＝﹣2x+y+x2﹣y2，故本选项错误，不符合题意；
C、2x2﹣3（x﹣5）＝2x2﹣3x+15，故本选项错误，不符合题意；
D、﹣a3﹣[﹣4a2+（1﹣3a）]＝﹣a3+4a2﹣1+3a，故本选项正确，符合题意．
去括号正确的是D．
故选：D．
6．（3分）多项式7x2﹣4x+23的项数及次数是（ ）
A．3，3B．2，3C．3，2D．2，2
【解答】解：多项式7x2﹣4x+23是3个单项式的和，因此该多项式的项数是3；
组成多项式的单项式的最高次数是2，因此该多项式的次数是2．
故选：C．
7．（3分）在式子“﹣23〇（﹣1）2中的“〇”内填入下列运算符号，计算后结果最大的是（ ）
A．+B．﹣C．×D．÷
【解答】解：﹣23＝﹣8，
（﹣1）2＝1，
﹣8+1＝﹣7，
﹣8﹣1＝﹣9，
﹣8×1＝﹣8，
﹣8÷1＝﹣8，
∵﹣7＞﹣8＝﹣8＞﹣9，
∴计算结果最大的是﹣7，
故选：A．
8．（3分）若|x|＝3，|y|＝6，且x＞y，则x﹣y的值是（ ）
A．﹣3和﹣9B．3和﹣6C．﹣3和9D．3和9
【解答】解：∵|x|＝3，|y|＝6，
∴x＝±3，y＝±6，
∵x＞y，
∴x＝3，y＝﹣6或x＝﹣3，y＝﹣6，
当x＝3，y＝﹣6时，x﹣y＝3﹣（﹣6）＝9，
当x＝﹣3，y＝﹣6时，x﹣y＝﹣3﹣（﹣6）＝3，
∴x﹣y的值是3和9．
故选：D．
9．（3分）如图1是由8个同样大小的立方体组成的魔方，体积为64，图中阴影部分是一个正方形ABCD，现把正方形ABCD放到数轴上（如图2），使得A与﹣1重合，那么D在数轴上表示的数为（ ）
A．B．C．D．
【解答】解：∵＝4，
∴这个魔方的棱长为4，
∴小立方体的棱长为2，
∴正方形ABCD的面积为：×2×2×4＝8，
∴边长为，
∴D在数轴上表示的数为﹣1﹣．
故选：C．
10．（3分）如图，在一个大长方形中放入三个边长不等的小正方形①、②、③，若要求出两个阴影部分周长的差，只要知道下列哪个图形的面积（ ）
A．正方形①B．正方形②C．正方形③D．大长方形
【解答】解：如图，
设HI＝x，HN＝y，正方形①的边长为a，正方形②的边长为b，正方形③的边长为c，
∴ON＝a﹣x，NE＝b﹣y，PD＝c+b﹣x，PI＝a﹣y，IG＝b﹣x，GR＝b﹣c，RS＝c，DS＝a+b﹣y﹣c，
∴C六边形PIGRSD＝PI+IG+GR+RS+DS+PD＝a﹣y+b﹣x+b﹣c+c+a+b﹣y﹣c+b+c﹣x＝2a﹣2y+4b﹣2x，
C四边形OBEN＝ON+OB+BE+NE＝a﹣x+b﹣y+a﹣x+b﹣y＝2a﹣2x+2b﹣2y，
∴C六边形PIGRSD﹣C四边形OBEN＝2b，
∴只要知道正方形②的边长b，就可以求出两个阴影部分周长的差．
∴只要知道正方形②的面积，就可求出两个阴影部分周长的差．
故选：B．
二、填空题（本题有6小题，共24分）
12．（4分）近似数3.0万精确到 千 位．
【解答】解：近似数3.0万精确到千位．
故答案为：千．
13．（4分）在①﹣2.5，②，③3.1415926，④1.212212221…（每两个1之间依次多一个2），⑤，⑥，⑦，⑧中，分数有 ①③⑤ ；无理数有 ②④⑥ （只填序号）
【解答】解：①﹣2.5是有限小数，可以化成分数；
②是无理数；
③3.1415926是有限小数，可以化成分数；
④1.212212221…（每两个1之间依次多一个2）是无理数；
⑤是分数；
⑥是无理数；
⑦是整数；
⑧是整数，
∴分数有①③⑤；无理数有②④⑥．
故答案为：①③⑤；②④⑥．
14．（4分）已知（m+4）2+|n﹣5|＝0，则mn＝ ﹣20 ．
【解答】解：∵（m+4）2+|n﹣5|＝0，（m+4）2≥0，|n﹣5|≥0，
∴m+4＝0，n﹣5＝0，
解得m＝﹣4，n＝5，
∴mn＝﹣4×5＝﹣20．
故答案为：﹣20．
15．（4分）若x是最大的负整数，y是最小的正整数，z是平方根等于本身的数，则x﹣y﹣z的值是 ﹣2 ．
【解答】解：∵x是最大的负整数，
∴x＝﹣1，
∵y是最小的正整数，
∴y＝1，
∵z是平方根等于本身的数，
∴z＝0，
∴x﹣y﹣z＝﹣1﹣1﹣0＝﹣2，
故答案为：﹣2．
16．（4分）已知：，且abc＞0．则m＝ 6或﹣2或0或﹣4 ．
【解答】解：∵abc＞0，
∴a、b、c为三个正数，或一个正数，两个负数，
①当a＞0，b＞0，c＞0时，，
②当a＞0，b＜0，c＜0时，，
③当a＜0，b＞0，c＜0时，，
④当a＜0，b＜0，c＞0时，，
故答案为：6或﹣2或0或﹣4．
三、简答题（本题有7小题，共66分）
17．（12分）计算：
（1）3﹣7﹣（﹣12+23）；
（2）（请用简便方法计算）；
（3）；
（4）．
【解答】解：（1）3﹣7﹣（﹣12+23）
＝3﹣7+12﹣23
＝（3+12）﹣（7+23）
＝15﹣30
＝﹣15；
（2）
＝
＝
＝﹣6；
（3）
＝
＝
＝﹣6×6
＝﹣36；
（4）
＝
＝．
18．（6分）（1）先化简，再求值：，其中a＝2，b＝﹣3．
（2）已知2x+y＝3，求代数式3（x﹣2y）+5（x+2y﹣1）﹣2的值．
【解答】解：（1）
＝2a2+2ab﹣2a2+3ab
＝5ab．
当a＝2，b＝﹣3时，
原式＝5×2×（﹣3）
＝﹣30．
（2）3（x﹣2y）+5（x+2y﹣1）﹣2
＝3x﹣6y+5x+10y﹣5﹣2
＝8x+4y﹣7．
∵2x+y＝3，
∴原式＝4（2x+y）﹣7
＝4×3﹣7
＝12﹣7
＝5．
19．（8分）义乌“8.2”疫情爆发后火速蔓延，根据疫情防控形势，东阳防控指挥部连续一段时间在全市范围开展全员核酸检测．为方便大家做核酸，各街道小区增设多个检测点．某便民检测点在8月8日当天共检测1800人次，在接下来的8月9日﹣8月15日的一周内，记录每天核酸检测人数相比前一天的增减情况如下表：（单位：人）
注：正号表示检测人数比前一天增加，负号表示检测人数比前一天减少．
（1）8月9日﹣8月15日的这一周内检测人数最多的是哪天？这天检测了多少人？
（2）8月9日﹣8月15日的这一周内检测人数最多的一天比人数最少的一天多检测多少人？
（3）在排队等候做核酸的过程中，小东观察到一个医务人员给一人做检测需要10秒，那么8月10日这天若只安排一个医务人员工作，从17：30开始到22：30能完成检测任务吗（不考虑其他准备时间）？
【解答】解：（1）9日：1800+180＝1980（人），
10日：1980﹣200＝1780（人），
11日：1780+300＝2080（人），
12日：2080﹣130＝1950（人），
13日：1950﹣50＝1900（人），
14日：1900+150＝2050（人），
15日：2050+50＝2100（人），
答：这一周内检测人数最多的是8月15日，检测了2100人；
（2）2100﹣1780＝320（人），
答：这一周内检测人数最多的一天比人数最少的一天多检测320人；
（3）能完成，
1780×10+3600≈4.944（小时），
4.944小时＜5小时，所以可以完成．
20．（8分）现定义新运算“⊙”，对于任意两个实数a，b，规定a⊙b＝ab﹣2a﹣2b．
（1）计算：3⊙5；
（2）若a⊙（3⊙k）的取值与a无关，求实数k．
【解答】解：（1）根据定义的新运算，
可得3⊙5＝3×5﹣2×3﹣2×5＝﹣1；
（2）∵3⊙k＝3k﹣2×3﹣2k＝k﹣6，
∴a⊙（3⊙k）＝a⊙（k﹣6）＝a（k﹣6）﹣2a﹣2（k﹣6）＝（k﹣8）a﹣2k+12，
∵a⊙（3⊙k）的取值与a无关，
∴k﹣8＝0，
解得k＝8．
21．（8分）已知，则的整数部分为1；而减去其整数部分的差就是的小数部分，则的小数部分为．根据以上的内容，解答下面的问题：
（1）填空：的整数部分是 4 ，的小数部分是 ﹣4 ．
（2）若，其中是m为整数，且0＜n＜1，求m﹣n的值．
【解答】解：（1）∵16＜23＜25，
∴，即，
∴的整数部分是4，
∵16＜19＜25，
∴，即，
∴的整数部分为4，的小数部分为，
故答案为：4，；
（2）∵25＜34＜36，
∴，即，
∴，
∴，
∵m是整数，且0＜n＜1，
∴，
∴．
22．（12分）若数轴上的点A、点B表示的数分别为a、b，则A、B两点之间的距离AB＝|a﹣b|，线段AB的中点表示的数为．如图：现数轴上有一点A表示的数为﹣10，点B表示的数为18，点P从点A出发，以每秒4个单位长度的速度沿数轴向右匀速运动，同时点Q从点B出发，以每秒3个单位长度的速度向左匀速运动，设运动时间为t秒．
（1）A、B两点之间的距离AB＝ 28 ，线段AB的中点表示的数为 4 ．
（2）当t＝ 4 时，P、Q两点相遇，相遇点所表示的数为 6 ．
（3）求当t为何值时，．
【解答】解：（1）AB＝|a﹣b|＝|（﹣10）﹣18|＝28，
线段AB的中点表示的数为：，
故答案为：28，4；
（2）根据题意可得：
AP＝4t，BQ＝3t，
当P、Q两点相遇时，AP+BQ＝AB，
∴4t+3t＝28，解得：t＝4，
∴相遇点所表示的数为：﹣10+4×4＝6，
故答案为：4，6；
（3）∵AB＝28，
∴，
①当点P、Q还未相遇时：4t+3t＝28﹣14，
解得：t＝2；
②当点P、Q相遇后：4t+3t＝28+14，
解得：t＝6；
综上：t＝2或t＝6．
23．（12分）某校需要订购中考专用的某款跳绳和排球，经调查发现，该款跳绳、排球各商家均标价为50元/条，40元/个，现有3家商店在做促销活动如下表：
（1）若在乙店购买10套，则总费用 850 元；在乙店购买40套，则总费用 3200 元．
（2）若现在需要跳绳a条和排球a个，且仅在一家商店购买，请用含a的代数式分别表示甲、乙两店的总费用．
甲店总费用： 81a元 ；
乙店总费用：当0＜a≤30时， 85a元 ；当30＜a≤60时， （100a﹣0.5a2）元 ；当a＞60时， 75a元 ．
（3）当需要购买60条跳绳和120个排球时，请你通过计算设计一种最省钱的购买方案，并求出总费用．
【解答】解：（1）若在乙店购买10套，则总费用85×10＝850（元）；
在乙店购买40套，每套的价格是85﹣10×0.5＝80，则总费用是40×80＝3200（元）；
故答案为：850；3200；
（2）甲店总费用是：（50a+40a）×90%＝81a元；
乙店总费用：当0＜a≤30时，85a元；
当30＜a≤60时，a[85﹣0.5（a﹣30）]＝（100a﹣0.5a2）元；
当a＞60时，75a元；
故答案为：81a元；85a元，（100a﹣0.5a2）元，75a元；
（3）若只在甲店购买，所需费用是：81×60+60×40×0.9＝7020（元）；
若只在乙店购买，所需费用是：100×60﹣0.5×602+40×60＝6600（元）；
若在丙店购买45个排球，送9个排球，剩下的在甲店购买，则所需费用是：
45×40+60×50×0.9+66×40×0.9＝6876（元）；
若在丙店购买45个排球，送9个排球，剩下的在乙店购买，则所需费用是：
100×60﹣0.5×602+45×40+6×40＝6240（元）；
若在乙店购买60套，丙店购买45个排球，送9个排球，在甲店购买6个排球，所需费用是：100×60﹣0.5×602+45×40+6×40×0.9＝6216（元）；
综上，最省钱的购买方案是在乙店购买60套，丙店购买45个排球，送9个排球，在甲店购买6个排球，总费用是6216元．
四、选择题（共1小题，每小题3分，满分3分）
24．（3分）已知当x＝1时，3ax3+bx2﹣2cx+4＝8，且ax3+2bx2﹣cx﹣15＝﹣14，则当x＝﹣1时，5ax3﹣5bx2﹣4cx+2022＝（ ）
A．2016B．2017C．2018D．2020
【解答】解：∵当x＝1时，3ax3+bx2﹣2cx+4＝8，且ax3+2bx2﹣cx﹣15＝﹣14，
∴，
①﹣②×3得：﹣5b+c＝1③，
②﹣①×2得：﹣5a+3c＝﹣7④，
③+④得：﹣5a﹣5b+4c＝﹣6，
当x＝﹣1时，
5ax3﹣5bx2﹣4cx+2022
＝﹣5a﹣5b+4c+2022
＝﹣6+2022
＝2016，
故选：A．
五、填空题（共3小题，每小题3分，满分9分）
25．（3分）若a、b、c、d是互不相等的整数（a＜b＜c＜d），且abcd＝121，则ac+bd＝ ﹣12 ．
【解答】解：已知a、b、c、d是互不相等的整数，且abcd＝121，
又121＝11×11，那么a，b，c，d四个整数之积等于121，
只有，﹣11，﹣1，1，11，
又已知a＜b＜c＜d，
所以，a＝﹣11，b＝﹣1，c＝1，d＝11，
那么，ac+bd＝（﹣11）1+（﹣1）11＝﹣11﹣1＝﹣12．
故答案为：﹣12．
26．（3分）已知|2009﹣a|+＝a，则a﹣20092＝ 2010 ．
【解答】解：根据二次根式有意义的条件，得
a﹣2010≥0，
则a≥2010．
又|2009﹣a|+＝a，
∴a﹣2009+＝a，
＝2009，
a﹣2010＝20092，
∴a﹣20092＝2010．
故答案为2010．
27．（3分）已知动点A从原点O出发沿数轴向左运动，同时动点B也从原点出发沿数轴向右运动，动点A的速度为每秒1个单位长度，动点B的速度为每秒2个单位长度，5秒后动点B调转方向向左运动，A、B两点的速度仍保持不变，则 或10或或20 秒后A、B、O三点中一点到另两个点的距离相等．
【解答】解：设运动时间为t秒．
当0＜t≤5时，点A表示的数为﹣t，点B表示的数为2t，点O在线段AB上（不包含顶点），
∴OA＝t，OB＝2t，
∴不存在OA＝OB的情况；
当5＜t＜10时，点A表示的数为﹣t，点B表示的数为2×5﹣2（t﹣5）＝20﹣2t，点O在线段AB上（不包含顶点），
∴OA＝0﹣（﹣t）＝t，OB＝20﹣2t，
根据题意得：t＝20﹣2t，
解得：t＝；
当t＝10时，点B，O重合，此时AO＝AB；
当10＜t＜20时，点A表示的数为﹣t，点B表示的数为2×5﹣2（t﹣5）＝20﹣2t，点B在线段OA上（不包含顶点），
∴AB＝20﹣2t﹣（﹣t）＝20﹣t，OB＝0﹣（20﹣2t）＝2t﹣20，
根据题意得：20﹣t＝2t﹣20，
解得：t＝；
当t＝20时，点A，B重合，此时AO＝BO；
当t＞20时，点A表示的数为﹣t，点B表示的数为2×5﹣2（t﹣5）＝20﹣2t，点A在线段OB上（不包含顶点），
∴OA＝0﹣（﹣t）＝t，AB＝﹣t﹣（20﹣2t）＝t﹣20，
∴不存在OA＝AB的情况．
综上所述，当t＝或10或或20时，A、B、O三点中一点到另两个点的距离相等．
故答案为：或10或或20．
日期
8.9
8.10
8.11
8.12
8.13
8.14
8.15
增减
+180
﹣200
+300
﹣130
﹣50
+150
+50
商店
促销活动
甲
库存充裕，全场9折
乙
库存充裕，按套数（即1条跳绳和上个排球）优惠：
30套以内（包括30套），每套85元；超过30套，每增加1套，所有套数每套降价0.5元，但每套降幅不超过15元
丙
仅库存排球55个，排球每满5个送1个
日期
8.9
8.10
8.11
8.12
8.13
8.14
8.15
增减
+180
﹣200
+300
﹣130
﹣50
+150
+50
商店
促销活动
甲
库存充裕，全场9折
乙
库存充裕，按套数（即1条跳绳和上个排球）优惠：
30套以内（包括30套），每套85元；超过30套，每增加1套，所有套数每套降价0.5元，但每套降幅不超过15元
丙
仅库存排球55个，排球每满5个送1个