

陕西省榆林市定边县第七中学2023-2024学年八年级上学期期中数学试题
展开这是一份陕西省榆林市定边县第七中学2023-2024学年八年级上学期期中数学试题,文件包含第23章小结与复习上课课件pptx、第23章小结与复习教案doc、第23章旋转单元测试docx等3份课件配套教学资源,其中PPT共36页, 欢迎下载使用。
八年级数学(北师大版)
考生注意:
本试卷共6页,满分120分,时间120分钟.
一、选择题(共8小题,每小题3分,计24分.每小题只有一个选项是符合题目要求的)
1.下列各数中,是无理数的是( )
A. B. C. D.0
2.下列各组长度的线段中,能够组成直角三角形的一组是( )
A.2,2,2B.6,8,10C.1,1, D.1,2,3
3.若点在函数的图象上,则k的值为( )
A.-5B.5C.-4D.4
4.下面分别给出了变量x与y之间的对应关系,其中y不是x的函数的是( )
A.B.C.D.
5.若二次根式在实数范围内有意义,则x的取值范围是( )
A. B. C. D.
6.课间操时,小华、小军、小刚的位置如图所示,小华的位置用表示,小军的位置用表示,那么小刚的位置可以表示成( )
(第6题图)
A. B. C. D.
7.在平面直角坐标系中,若将一次函数的图象向下平移6个单位后,得到一个正比例函数的图象,则m的值为( )
A.-4 B.4 C.-7 D.7
8.如图是用4个全等的直角三角形与1个小正方形拼成的正方形图案,已知大正方形的面积为49,小正方形的面积为4,若用x,y表示直角三角形的两条直角边长(),下列四个说法:
①;②;③;④.其中正确的是( )
(第8题图)
A.①② B.②④ C.③④ D.①②③④
二、填空题(共5小题,每小题3分,计15分)
9.化简:______.
10.在平面直角坐标系中,点与点关于x轴对称,则的值为______.
11.已知直线上有两点,,则与的大小关系是______.(填“>”“<”或“=”)
12.“黄金1号”玉米种子的价格为5元/kg,如果一次购买3 kg以上,超过3 kg部分的种子的价格打八折,设购买种子的数量为x kg,付款金额为y元,则y与x之间的函数表达式为______.
13.如图,点E,F分别在AB,CD上,于点O,.若,,则点F到直线AB的距离为______.
(第13题图)
三、解答题(共13小题,计81分,解答应写出过程)
14.(5分)计算:.
15.(5分)计算:.
16.(5分)已知的平方根为±2,的立方根为3,求的值.
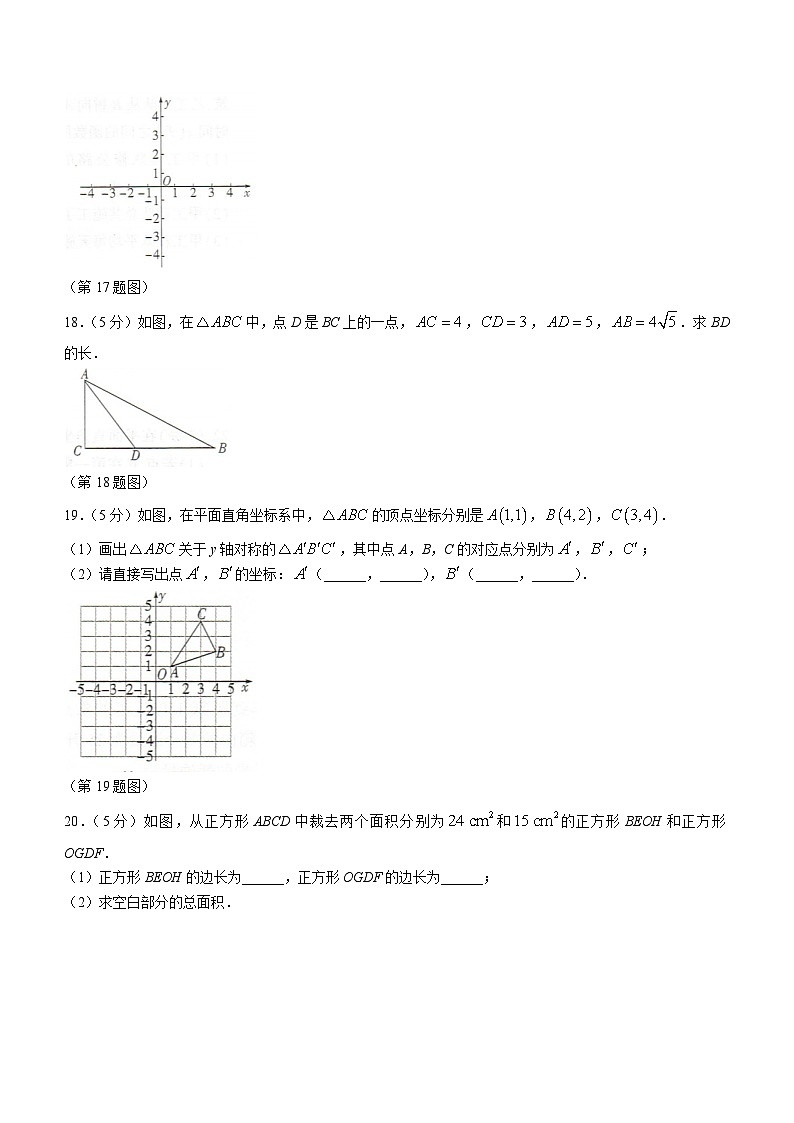
17.(5分)如图,在平面直角坐标系xOy中,一次函数的图象与x轴交于点A,与y轴交于点B.
(1)请在平面直角坐标系中画出该函数的图象;
(2)该函数图象与坐标轴围成图形的面积是______.
(第17题图)
18.(5分)如图,在中,点D是BC上的一点,,,,.求BD的长.
(第18题图)
19.(5分)如图,在平面直角坐标系中,的顶点坐标分别是,,.
(1)画出关于y轴对称的,其中点A,B,C的对应点分别为,,;
(2)请直接写出点,的坐标:(______,______),(______,______).
(第19题图)
20.(5分)如图,从正方形ABCD中裁去两个面积分别为和的正方形BEOH和正方形OGDF.
(1)正方形BEOH的边长为______,正方形OGDF的边长为______;
(2)求空白部分的总面积.
(第20题图)
21.(6分)某乡镇决定对A,B两村之间的公路进行改造,并有甲工程队从A村向B村方向修筑,乙工程队从B村向A村方向修筑.如图是甲、乙两个工程队修公路的长度y(米)与施工时间x(天)之间的函数图象,请根据图象所提供的信息回答下列问题:
(1)甲工程队修公路的长度总共有______米,乙工程队修公路的长度总共有______米;
(2)甲工程队总共施工了______天,乙工程队总共施工了天;
(3)甲工程队平均每天施工______米,乙工程队平均每天施工______米.
(第21题图)
22.(7分)在平面直角坐标系中,已知点,点.
(1)若点M在第一象限,且点M到x轴的距离与到y轴的距离相等,求m的值;
(2)若线段轴,求线段MN的长度.
23.(7分)周末,小丽一家人驾车到距家150千米的景点旅游.出发前,汽车油箱内的油量为35升,行驶了80千米时,油箱内的剩余油量为25升.
(1)汽车行驶过程中,平均每千米的耗油量为______升;
(2)直接写出油箱内的剩余油量y(升)与行驶路程x(千米)间的表达式;()
(3)当油箱中剩余油量为3升时,汽车的行驶路程是多少千米?
24.(8分)如图是游乐场新打造的一款儿童游戏项目,工作人员告诉小敏,该项目AB段和BC段均由不锈钢管材打造,总长度为26米,长方形ADCG和长方形DEFC均为木质平台的横截面,点G在AB上,点C在GF上,点D在AE上,经过现场测量得知:米,米.
(1)请求出立柱AB段的长度;
(2)为加强游戏安全性,游乐场打算再焊接一段钢索BF,经测量米,请你求出要焊接的钢索BF的长.
(第24题图)
25.(8分)某公司采购员到紫阳茶叶市场购买某品牌毛尖茶,商家推出了两种购买方式:
设该公司此次购买茶叶x kg,按方式一购买茶叶的总费用为元,按方式二购买茶叶的总费用为元.
(1)请直接写出,关于x的函数表达式;
(2)若按方式一购买茶叶的总费用和按方式二购买茶叶的总费用相同,则该公司此次购买了多少千克这种茶叶?
(3)若该公司此次购买茶叶的总预算为8 400元,则按照哪种方式购买可以获得更多的茶叶?
26.(10分)如图,在平面直角坐标系xOy中,点在正比例函数的图象上,过点A的另一条直线分别交x轴,y轴的正半轴于点B,C.
(1)m的值为______;
(2)若,求直线AB的函数表达式;
(3)在(2)的条件下,当动点P在线段OA和射线AC上运动时,是否存在点P,使得?若存在,求出此时点P的坐标;若不存在,请说明理由.
(第26题图)
试卷类型:A
2023~2024学年度第一学期期中检测
八年级数学参考答案及评分标准(北师大版)
一、选择题(共8小题,每小题3分,计14分,每小题只有一个选项是符合题目要求的)
二、填空题(共5小题,每小题3分,计15分)
9. 10.1 11.> 12. 13.
三、解答题(共13小题,计81分.解答应写出过程)
14.解:.
15.解:.
16.解:因为的平方根为±2,的立方根为3,所以,.
所以,.所以.
17.解:(1)当时,,即.
当时,,即.
画图如下:
(2)2.
18.解:∵,,∴.
∵是直角三角形,且.
∵在中,,∴.
∴.
19.解:(1)如图,即为所求.
(2),.
20.解:(1), .
(2).
答:空白部分的面积为.
21.解:(1)750,600.
(2)10,4.
(3)75,150.
22.解:(1)因为M在第一象限,点M到x轴的距离与到y轴的距离相等,
所以.解得.
(2)因为线段轴,所以M,N点的纵坐标相等,
即,解得.所以.
所以线段MN的长度为.
23.解:(1)0.125.
(2)根据题意,得.
(3)当时,,解得.
答:当油箱中剩余油量为3升时,汽车的行驶路程是256千米.
24.解:(1)根据题意,得米,米,
设米,则米.
在中,根据勾股定理,得,即.
解得.∴米.
∴(米).
答:立柱AB段的长度为9米.
(2)根据题意,得米,∴(米).
在中,根据勾股定理,得(米).
答:要焊接的钢索BF的长为米.
25.解:(1)根据题意,得,.
(2)根据题意,得.
解得.
答:该公司此次购买了1 kg这种茶叶.
(3)若按照第一种方式购买茶叶,则,解得.
若按照第二种方式购买茶叶,则,解得.
∵,∴按照第一种方式购买可以获得更多的茶叶.
答:若该公司此次购买茶叶的总预算为8 400元,则按照第一种方式购买可以获得更多的茶叶.
26.解:(1).
(2)设,,
∵,,∴,解得.∴.
设直线AB的函数表达式为,点,在直线AB上,代入得,.
将代入,解得.
∴直线AB的函数表达式为.
(3)存在.
设,则中OC边上的高为,由(2)可知,
∴.
当动点在线段OA上时,,如图①,
∴,解得.
∵在线段OA上,∴由(1)可知.
当动点在射线AC上运动时,如图②,
∴,解得.
当时,,∴.
当时,,∴.
综上所述,存在点P的坐标为或或,使得.
会员卡费用(元/张)
茶叶价格(元/kg)
方式一:会员
500
1 600
方式二:非会员
0
2 100
题号
1
2
3
4
5
6
7
8
选项
A
B
D
A
B
C
D
C
相关试卷
这是一份陕西省榆林市定边县定边县第七中学2023-2024学年九年级上学期期末数学试题,共1页。
这是一份陕西省榆林市定边县定边县第七中学2023-2024学年九年级上学期期末数学试题(含解析),共22页。试卷主要包含了选择题,四象限,则的值可能是,解答题等内容,欢迎下载使用。
这是一份陕西省榆林市+定边县第七中学2023-2024学年九年级上学期期末数学试题,共11页。试卷主要包含了本试卷共6页,满分120分;,若,则________等内容,欢迎下载使用。












