广东省潮州市饶平县2022-—2023学年下学期八年级期中数学试卷

这是一份广东省潮州市饶平县2022-—2023学年下学期八年级期中数学试卷，共2页。
一．选择题（共10小题，满分30分，每小题3分）
1．（3分）下列二次根式中，最简二次根式是（ ）
A．﹣B．C．D．
2．（3分）下列各组数据中，不能作为直角三角形边长的是（ ）
A．3，4，5B．5，12，13C．3，5，7D．1，2，
3．（3分）下列运算正确的是（ ）
A．•＝B．9×＝C．×＝12D．•＝6
4．（3分）下列说法不正确的是（ ）
A．两组对边分别平行的四边形是平行四边形
B．一组对边平行，另一组对边相等的四边形是平行四边形
C．一组对边平行且相等的四边形是平行四边形
D．一组对边平行，一组对角相等的四边形是平行四边形
5．（3分）如图，在平坦的地面上，为测量位于水塘旁的两点A，B间的距离，先确定一点O，分别取OA，OB的中点C，D，量得CD＝40m，则A，B之间的距离是（ ）
A．20mB．40mC．80mD．100m
6．（3分）如图所示，DE为△ABC的中位线，点F在DE上，且∠AFB＝90°，若AB＝6，BC＝8，则EF的长为（ ）
A．1B．2C．1.5D．2.5
7．（3分）如图，在△ABC中，D为BC的中点，E为AD的中点，过点A作BC的平行线交CE的延长线于点F，连接BF，则下列结论错误的是（ ）
A．四边形ACDF是平行四边形
B．若AB＝AC，则DF＝AB
C．若，则四边形ACDF为菱形
D．若∠BAC＝90°，则CF＝AD
8．（3分）下面命题中，真命题是（ ）
A．等边三角形既是轴对称图形又是中心对称图形
B．三角形的内心是三角形三条中线的交点
C．有两边一角对应相等的三角形一定全等
D．等腰三角形的周长为l，腰长为x，则
9．（3分）如图，在Rt△ABC中，∠ACB＝90°，点D，E分别是边AB，AC的中点，延长BC至F，使CF＝BC，若AB＝10，则EF的长是（ ）
A．5B．4C．3D．2
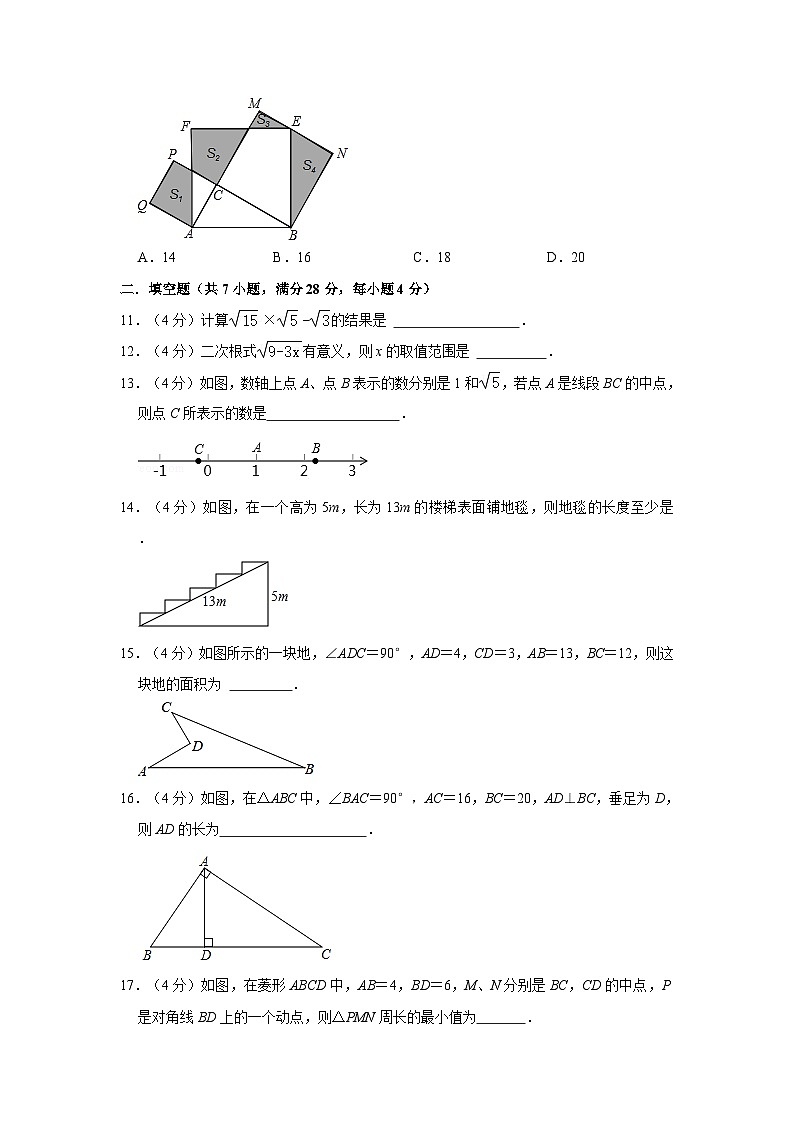
10．（3分）如图，Rt△ABC中，∠C＝90°，AC＝3，BC＝4．分别以AB、AC、BC为边在AB的同侧作正方形ABEF、ACPQ、BCMN，四块阴影部分的面积分别为S1、S2、S3、S4．则S1+S2+S3+S4等于（ ）
A．14B．16C．18D．20
二．填空题（共7小题，满分28分，每小题4分）
11．（4分）计算的结果是 ．
12．（4分）二次根式有意义，则x的取值范围是 ．
13．（4分）如图，数轴上点A、点B表示的数分别是1和，若点A是线段BC的中点，则点C所表示的数是 ．
14．（4分）如图，在一个高为5m，长为13m的楼梯表面铺地毯，则地毯的长度至少是 ．
15．（4分）如图所示的一块地，∠ADC＝90°，AD＝4，CD＝3，AB＝13，BC＝12，则这块地的面积为 ．
16．（4分）如图，在△ABC中，∠BAC＝90°，AC＝16，BC＝20，AD⊥BC，垂足为D，则AD的长为 ．
17．（4分）如图，在菱形ABCD中，AB＝4，BD＝6，M、N分别是BC，CD的中点，P是对角线BD上的一个动点，则△PMN周长的最小值为 ．
三．解答题（共8小题，满分62分）
18．（6分）计算．
19．（6分）如图，在四边形ABCD中，∠1＝∠2，∠3＝∠4．
求证：四边形ABCD是平行四边形．
20．（6分）如图，△ABC的中线BD、CE交于点O，F、G分别是BO、CO的中点，试说明EFDG．
21．（8分）已知：x＝2+，y＝2﹣．
（1）求代数式：x2+3xy+y2的值；
（2）若一个菱形的对角线的长分别是x和y，求这个菱形的面积？
22．（8分）如图，在矩形ABCD中，AB＝5，在CD边上找一点E，沿直线AE把△ADE折叠，使得点D恰好落在BC边上的点F处，且BF＝12．解答下列问题：
（1）求AD的长．
（2）求△ADE的面积．
23．（8分）如图，在△ABC中，∠ACB＝90°，点D在AB边上且AD＝BD，连接CD，E是CD的中点，过点C作CF∥AB，交AE的延长线于点F，连接BF．
（1）求证：AE＝EF；
（2）求证：四边形BDCF是菱形；
（3）当∠ABC＝45°时，四边形BDCF是 ．
24．（10分）问题情境：在综合与实践课上，同学们以“已知三角形三边的长度，求三角形面积”为主题开展数学活动，小颖想到借助正方形网格解决问题．图1，图2都是8×8的正方形网格，每个小正方形的边长均为1，每个小正方形的顶点称为格点．
操作发现：小颖在图1中画出△ABC，其顶点A，B，C都是格点，同时构造正方形BDEF，使它的顶点都在格点上，且它的边DE，EF分别经过点C，A，她借助此图求出了△ABC的面积．
（1）在图1中，小颖所画的△ABC的三边长分别是AB＝ ，BC＝ ，AC＝ ；△ABC的面积为 ．
解决问题：
（2）已知△ABC中，AB＝，BC＝2，AC＝5，请你根据小颖的思路，在图2的正方形网格中画出△ABC，并直接写出△ABC的面积．
25．（10分）在矩形ABCD中，AB＝12，P是边AB上一点，把△PBC沿直线PC折叠，顶点B的对应点是点G，过点B作BE⊥CG，垂足为E且在AD上，BE交PC于点F．
（1）如图1，若点E是AD的中点，求证：△AEB≌△DEC；
（2）如图2，当AD＝25，且AE＜DE时，求的值；
（3）如图3，当BE•EF＝108时，求BP的值．
参考答案与试题解析
一．选择题（共10小题，满分30分，每小题3分）
1． 解：A、﹣，是最简二次根式，符合题意；
B、＝＝2，被开方数中含能开得尽方的因数，不是最简二次根式，不符合题意；
C、＝，被开方数含分母，不是最简二次根式，不符合题意；
D、＝|a|，被开方数中含能开得尽方的因式，不是最简二次根式，不符合题意；
故选：A．
2． 解：A、32+42＝52，根据勾股定理的逆定理可知是直角三角形，故本选项不符合题意；
B、52+122＝132，根据勾股定理的逆定理可知是直角三角形，故本选项不符合题意；
C、32+52≠72，根据勾股定理的逆定理可知不是直角三角形，故本选项符合题意；
D、，根据勾股定理的逆定理可知是直角三角形，故本选项不符合题意；
故选：C．
3． 解：A、•＝，故此选项错误；
B、9×＝9＝9×＝3，故此选项错误；
C、×＝2，故此选项错误；
D、•＝＝6，故此选项正确；
故选：D．
4． 解：A、∵两组对边分别平行的四边形是平行四边形，
∴选项A不符合题意；
B、∵一组对边平行，另一组对边相等的四边形不一定是平行四边形，
∴选项B符合题意；
C、∵一组对边平行且相等的四边形是平行四边形，
∴选项C不符合题意；
D、∵一组对边平行，一组对角相等的四边形是平行四边形，
∴选项D不符合题意；
故选：B．
5． 解：∵点C，D为OA，OB的中点，
∴CD是△AOB的中位线，
∴AB＝2CD，
∵CD＝40m，
∴AB＝2CD＝80（m），
故选：C．
6． 解：∵DE是△ABC的中位线，BC＝8，
∴，D是AB的中点，
∵∠AFB＝90°，
∴，
∴EF＝DE﹣DF＝1，
故选：A．
7． 解：A、∵D为BC的中点，E为AD的中点，
∴AE＝DE，BD＝CD，
∵AF∥BC，
∴∠FAE＝∠CDE，
在△AEF和△DEC中，
，
∴△AEF≌△DEC（ASA），
∴AF＝CD，
∴AF＝BD＝CD，
∵AF∥BC，
∴四边形ACDF和四边形ADBF都是平行四边形，故选项A不符合题意；
B、∵AB＝AC，BD＝CD，
∴AD⊥BC，
∴平行四边形ADBF是矩形
∴DF＝AB，故选项B不符合题意；
C、∵AC＝BC，BD＝CD，
∴CD＝AC，
∴平行四边形ACDF是菱形，故选项C不符合题意；
D、∵∠BAC＝90°，BD＝CD，
∴AD＝BC＝CD，故选项D符合题意；
故选：D．
8． 解：A、等边三角形既是轴对称图形，但不是中心对称图形，原命题是假命题；
B、三角形的内心是三角形三条角平分线的交点，原命题是假命题；
C、有两边及其夹角对应相等的三角形一定全等，原命题是假命题；
D、等腰三角形的周长为l，腰长为x，则，是真命题；
故选：D．
9． 解：∵AD＝DB，AE＝EC，
∴DE∥BC，DE＝BC，
∵CF＝BC，
∴DF∥CF，DF＝CF，
∴四边形DEFC是平行四边形，
∴EF＝CD，
∵∠ACB＝90°，AD＝DB，AB＝10，
∴CD＝AB＝5，
∴EF＝5．
故选：A．
10． 解：过F作AM的垂线交AM于D，
可证明Rt△ADF≌Rt△BCA，Rt△DFK≌Rt△CAT，
所以S2＝SRt△ABC．
由Rt△DFK≌Rt△CAT可进一步证得：Rt△FPT≌Rt△EMK，
∴S3＝S△FPT，
又可证得Rt△AQF≌Rt△ACB，
∴S1+S3＝SRt△AQF＝SRt△ABC．
易证Rt△ABC≌Rt△EBN，
∴S4＝SRt△ABC，
∴S1+S2+S3+S4
＝（S1+S3）+S2+S4
＝SRt△ABC+SRt△ABC+SRt△ABC
＝SRt△ABC×3
＝4×3÷2×3
＝18．
故选：C．
二．填空题（共7小题，满分28分，每小题4分）
11． 解：原式＝﹣
＝﹣
＝5﹣
＝4．
故答案为：4．
12． 解：二次根式有意义，则9﹣3x≥0，
故x的取值范围是x≤3．
故答案为：x≤3．
13． 解：设点C所表示的数是x，
∵点A是线段BC的中点，
∴AC＝AB，
∴1﹣x＝﹣1，
∴x＝2﹣．
即点C所表示的数是2﹣．
故答案为2﹣．
14． 解：由勾股定理得：
楼梯的水平宽度＝＝12，
∵地毯铺满楼梯是其长度的和应该是楼梯的水平宽度与垂直高度的和，
地毯的长度至少是12+5＝17米．
故答案为：17m．
15． 解：连接AC，
∵∠ADC＝90°，AD＝4，CD＝3，
∴AC2＝AD2+CD2＝42+32＝52，
∴AC＝5，
∵AB＝13，BC＝12，
∴AC2+BC2＝AB2，
∴∠ACB＝90°，
∴这块地的面积为：＝，
故答案为24．
16． 解：∵∠BAC＝90°，AC＝16，BC＝20，
∴AB＝＝12，
∵S△ABC＝AB•AC＝BC•AD，
∴×12×16＝×20AD，
∴AD＝．
故答案为：．
17． 解：如图，作ME⊥BD交AB于E，连接EN，与BD交于点P'，
当P与P'重合时，则EN就是PM+PN的最小值，
∵M、N分别是BC、CD的中点，
∴CN＝BM＝CM，
∵ME⊥BD交AB于E，
∴BE＝BM，
∴BE＝CN，BE∥CN，
∴四边形BCNE是平行四边形，
∴EN＝BC＝AB＝4，
∴DN＝NC，CM＝BM，
∴MN＝BD＝3，
∴△PMN的周长的最小值为4+3＝7．
故选答案为7．
三．解答题（共8小题，满分62分）
18． 解：原式＝﹣1﹣3﹣
＝﹣4．
19． 证明：∵∠1＝∠2，
∴AB∥CD．
∵∠3＝∠4，
∴AD∥BC．
∴四边形ABCD是平行四边形．
20． 证明：连接OA，如图所示：
∵△ABC的中线BD、CE交于点O，F、G分别是BO、CO的中点，
∴EF是△ABO的中位线，DG是△ACO的中位线，
∴EF∥OA，EF＝OA，DG∥OA，DG＝OA，
∴EFDG．
21． 解：（1）∵x＝2+，y＝2﹣，
∴x+y＝4，xy＝4﹣2＝2，
∴x2+3xy+y2＝（x+y）2+xy＝16+2＝18．
（2）S菱形ABCD＝xy＝（2+）（2﹣）＝1
22． 解：（1）在Rt△ABF中，AB＝5，BF＝12，由勾股定理得，
AF＝＝＝13，
由翻折变换可得，
AD＝AF＝13；
（2）由翻折变换得，ED＝EF，
设ED＝x，则EC＝5﹣x，FC＝BC﹣BG＝13﹣12＝1，
在Rt△EFC中，由勾股定理得，
EC2+FC2＝EF2，
即（5﹣x）2+12＝x2，
解得x＝，
即DE＝，
∴S△ADE＝AD•DE
＝×13×
＝，
答：△ADE的面积为．
23． （1）证明：∵CF∥AB，
∴∠DAE＝∠CFE，
∵E是CD的中点，
∴DE＝CE，
在△ADE和△FCE中，
，
∴△ADE≌△FCE（AAS），
∴AE＝EF．
（2）证明：∵△ADE≌△FCE，
∴AD＝FC，
∵AD＝BD，
∴FC＝BD，
∵FC∥BD，
∴四边形BDCF是平行四边形，
∵∠ACB＝90°，AD＝BD，
∴CD＝BD＝AB，
∴四边形BDCF是菱形．
（3）解：∵CD＝BD，∠ABC＝45°，
∴∠DCB＝∠DBC＝45°，
∴∠BDC＝90°，
∵四边形BDCF是菱形，
∴四边形BDCF是正方形，
故答案为：正方形．
24． 解：（1）AB＝＝5，BC＝＝，AC＝＝，
△ABC的面积为：4×4﹣×3×4﹣×1×4﹣×3×1＝，
故答案为：5；；；；
（2）△ABC的面积：7×2﹣×3×1﹣×4×2﹣×7×1＝5．
25． 解：（1）在矩形ABCD中，∠A＝∠D＝90°，AB＝DC，
∵E是AD中点，
∴AE＝DE，
在△AEB和△DEC中，
，
∴△AEB≌△DEC（SAS）；
（2）∵BE⊥CG，
∴∠BEC＝90°，
∴∠AEB+∠CED＝90°，
∵∠AEB+∠ABE＝90°，
∴∠CED＝∠ABE，
∵∠A＝∠D＝90°，
∴△ABE∽△DEC，
∴，
设AE＝x，
∴DE＝25﹣x，
∴，
∴x＝9或x＝16，
∵AE＜DE，
∴AE＝9，DE＝16，
∴CE＝20，BE＝15，
由折叠得，BC＝CG＝25，
在矩形ABCD，∠ABC＝90°，
∵△BPC沿PC折叠得到△GPC，
∴∠PGC＝∠PBC＝90°，∠BPC＝∠GPC，
∵BE⊥CG，
∴BE∥PG，
∴△ECF∽△GCP，
∴，
∴＝．
（3）如图，连接FG，
∵BE∥PG，
∴∠GPF＝∠PFB，
∴∠BPF＝∠BFP，
∴BP＝BF；
∵BP＝PG，
∴▱BPGF是菱形，
∴BP∥GF，
∴∠GFE＝∠ABE，
∴△GEF∽△EAB，
∴，
∴BE•EF＝AB•GF，
∵BE•EF＝108，AB＝12，
∴GF＝9，
∴BP＝GF＝9．