2024年高考数学第一轮复习精品导学案第30讲 y=sin(ωx+φ)的图象与性质（学生版）+教师版

这是一份2024年高考数学第一轮复习精品导学案第30讲 y=sin(ωx+φ)的图象与性质（学生版）+教师版，共2页。学案主要包含了2022年全国甲卷，2022年新高考1卷，2021年乙卷理科，2021年新高考1卷等内容，欢迎下载使用。
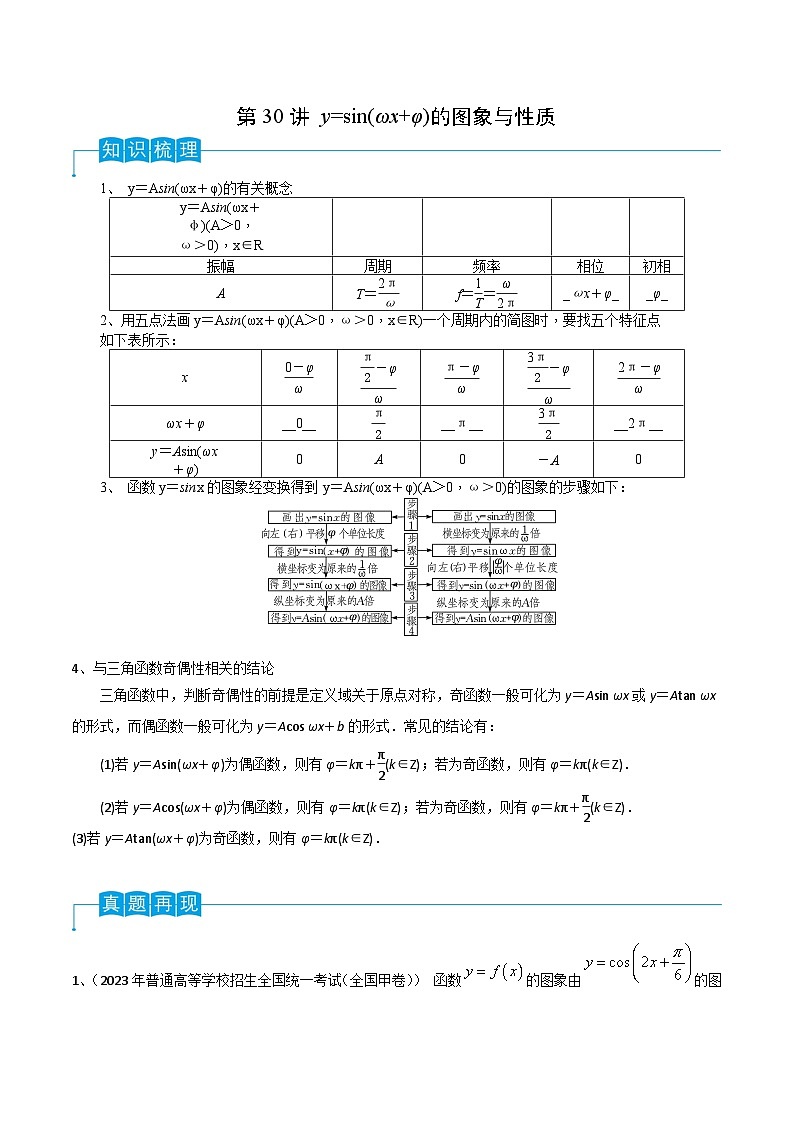
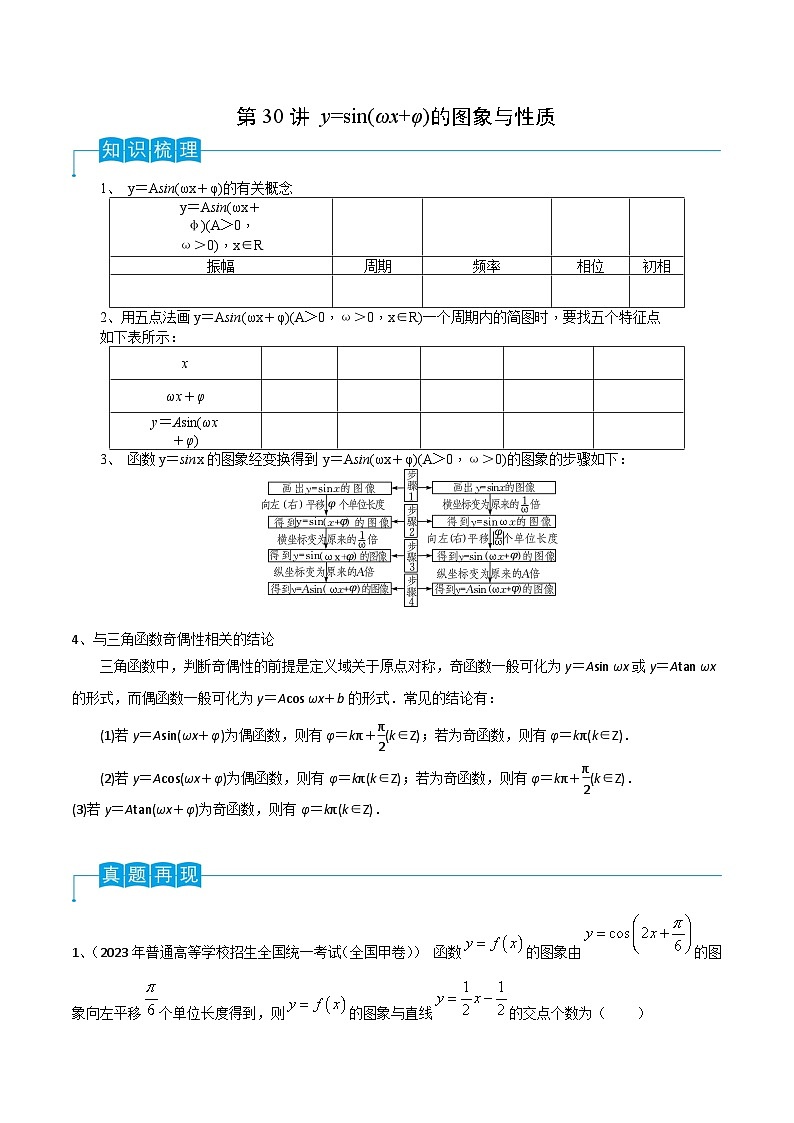
1、 y＝Asin(ωx＋φ)的有关概念
2、用五点法画y＝Asin(ωx＋φ)(A＞0，ω＞0，x∈R)一个周期内的简图时，要找五个特征点
如下表所示：
3、 函数y＝sinx的图象经变换得到y＝Asin(ωx＋φ)(A＞0，ω＞0)的图象的步骤如下：
4、与三角函数奇偶性相关的结论
三角函数中，判断奇偶性的前提是定义域关于原点对称，奇函数一般可化为y＝Asin ωx或y＝Atan ωx的形式，而偶函数一般可化为y＝Acs ωx＋b的形式．常见的结论有：
(1)若y＝Asin(ωx＋φ)为偶函数，则有φ＝kπ＋eq \f(π,2)(k∈Z)；若为奇函数，则有φ＝kπ(k∈Z)．
(2)若y＝Acs(ωx＋φ)为偶函数，则有φ＝kπ(k∈Z)；若为奇函数，则有φ＝kπ＋eq \f(π,2)(k∈Z)．
(3)若y＝Atan(ωx＋φ)为奇函数，则有φ＝kπ(k∈Z)．
1、（2023年普通高等学校招生全国统一考试（全国甲卷）） 函数的图象由的图象向左平移个单位长度得到，则的图象与直线的交点个数为（ ）
A. 1B. 2C. 3D. 4
【答案】C
【解析】
因为向左平移个单位所得函数为，所以，
而显然过与两点，
作出与的部分大致图象如下，

考虑，即处与的大小关系，
当时，，；
当时，，；
当时，，；
所以由图可知，与的交点个数为.
故选：C.
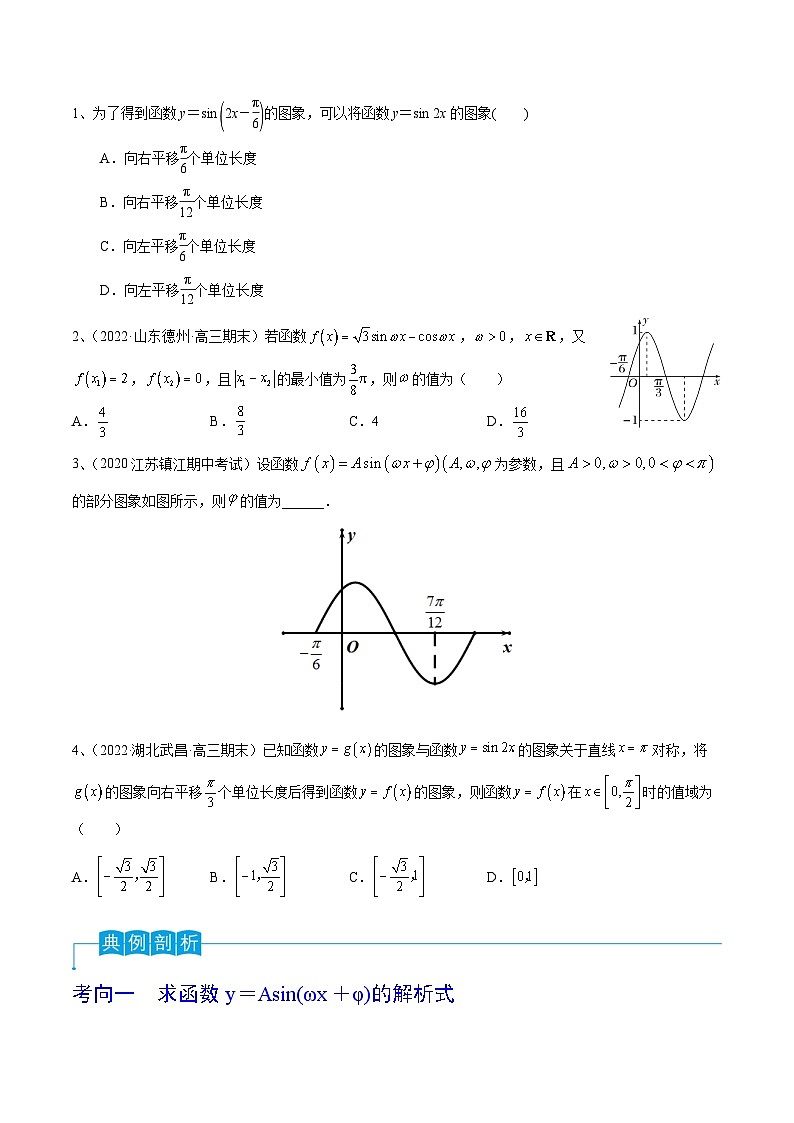
2、 （2023年普通高等学校招生全国统一考试（全国乙卷））已知函数在区间单调递增，直线和为函数的图象的两条对称轴，则（ ）
A. B. C. D.
【答案】D
【解析】
因为在区间单调递增，
所以，且，则，，
当时，取得最小值，则，，
则，，不妨取，则，
则
3、【2022年全国甲卷】将函数f(x)=sinωx+π3(ω>0)的图象向左平移π2个单位长度后得到曲线C，若C关于y轴对称，则ω的最小值是（ ）
A．16B．14C．13D．12
【答案】C
【解析】
由题意知：曲线C为y=sinωx+π2+π3=sin(ωx+ωπ2+π3)，又C关于y轴对称，则ωπ2+π3=π2+kπ,k∈Z，
解得ω=13+2k,k∈Z，又ω>0，故当k=0时，ω的最小值为13.
故选：C.
4、【2022年全国甲卷】设函数f(x)=sinωx+π3在区间(0,π)恰有三个极值点、两个零点，则ω的取值范围是（ ）
A．53,136B．53,196C．136,83D．136,196
【答案】C
【解析】
解：依题意可得ω>0，因为x∈0,π，所以ωx+π3∈π3,ωπ+π3，
要使函数在区间0,π恰有三个极值点、两个零点，又y=sinx，x∈π3,3π的图象如下所示：
则5π2